Triangle Congruence Proofs Made Easy: Practice Sheets

Triangle congruence proofs are an essential part of geometry, providing the foundation for understanding how shapes relate and fit together. Mastering these proofs isn't just about passing geometry class; it's about developing a deep understanding of spatial relationships and logical reasoning. This guide will take you through the process of creating and understanding triangle congruence proofs with a focus on practice sheets to enhance your learning experience.
The Basics of Triangle Congruence

Before diving into the proofs, let's revisit the basic theorems that establish triangle congruence:
- Side-Side-Side (SSS): If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
- Side-Angle-Side (SAS): If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, they are congruent.
- Angle-Side-Angle (ASA): If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, the triangles are congruent.
- Hypotenuse-Leg (HL): For right triangles, if the hypotenuse and one leg of one right triangle are congruent to the hypotenuse and one leg of another right triangle, the triangles are congruent.
- Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, the triangles are congruent.
📝 Note: Remember that AAA (Angle-Angle-Angle) and SSA (Side-Side-Angle) do not guarantee triangle congruence in all cases.
How to Approach Congruence Proofs

Here's a step-by-step guide to approaching triangle congruence proofs:
- Identify Given Information: Look at what is given in the problem or diagram.
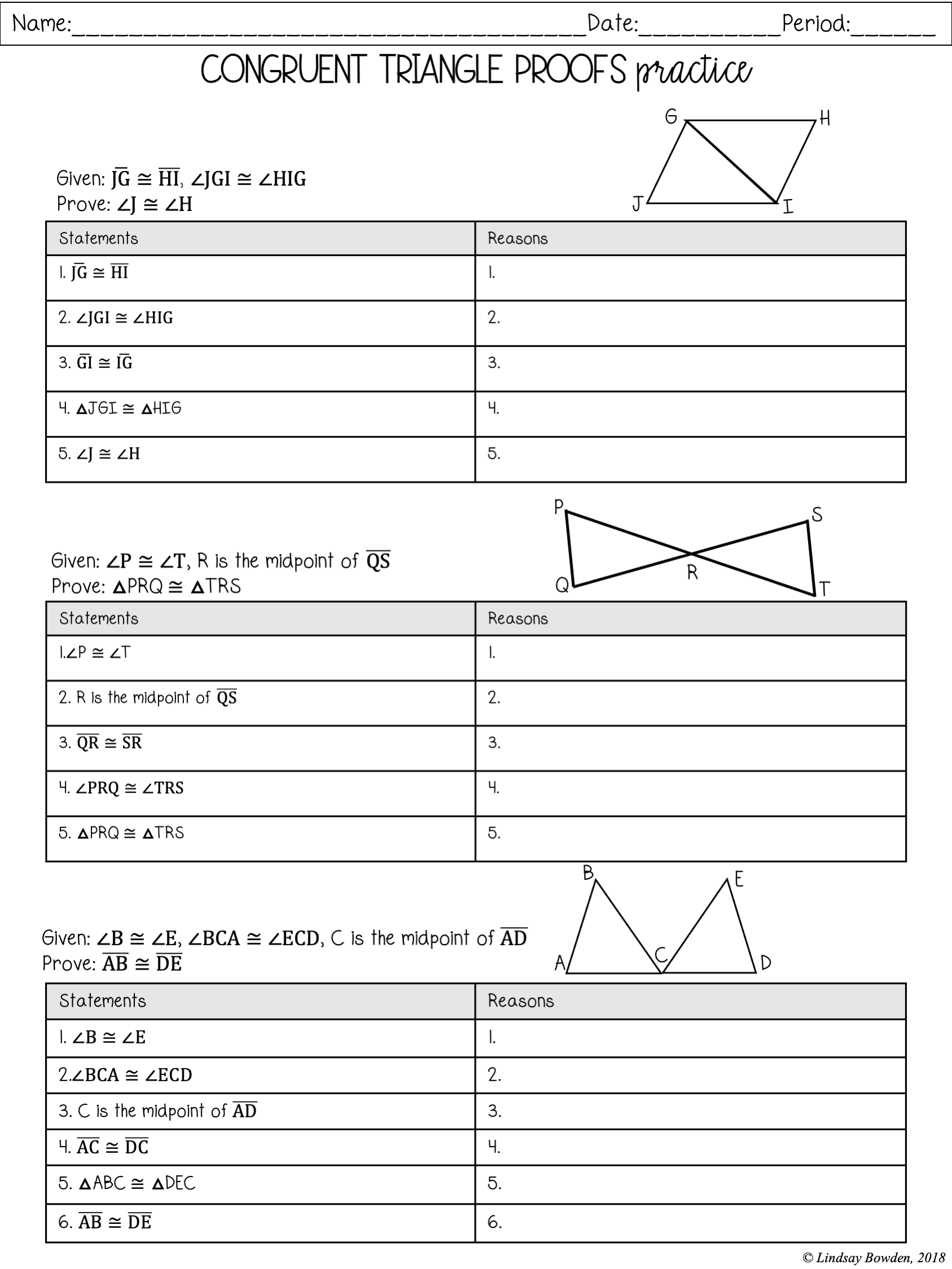
- State What Needs to be Proved: Clearly write down what you need to prove, such as "Triangle ABC is congruent to Triangle DEF."
- Apply Postulates: Determine which postulate or theorem can be applied based on the given information.
- Write Statements and Reasons:
- Statements: Detail each geometric fact or step used in the proof.
- Reasons: Provide the justification for each statement, referencing known postulates, theorems, or definitions.
- Conclude the Proof: Once you have enough information to justify congruence, conclude with "Therefore, Triangle ABC is congruent to Triangle DEF by the [postulate or theorem]."
📌 Note: Precision is key. Each statement must follow logically from the previous one, ensuring your proof is robust and correct.
Practice Sheets for Mastery

To become proficient in triangle congruence proofs, consistent practice is vital. Here are structured practice sheets that cater to various levels of difficulty:
Beginner's Sheet:

- Basic Proofs: Problems where all necessary information is given explicitly.
- Match Congruent Triangles: Matching pairs of triangles with given congruencies.
- Simple Statements: Fill in statements based on given diagrams.
📚 Note: Start with proofs that involve the simpler postulates like SSS or SAS before moving to more complex ones.
Intermediate Sheet:

- Multiple Steps: Proofs requiring several steps to reach the conclusion.
- Diagramming: Practice drawing your own diagrams based on given information.
- Postulate Identification: Identify which postulate could be used in different scenarios.
Advanced Sheet:

- Conditional Proofs: Proofs that might require logical reasoning outside the given information.
- Incorporating Other Theorems: Use the properties of isosceles triangles, midpoints, etc., in your proofs.
- Real-World Applications: Apply triangle congruence in context like architecture or engineering.
🔎 Note: Challenge yourself by attempting proofs without looking at the given answers or hints.
| Level | Key Skills to Practice |
|---|---|
| Beginner | Basic Congruence Postulates |
| Intermediate | Multiple Step Proofs, Drawing |
| Advanced | Conditional Proofs, Application |

Engaging with these practice sheets will not only help you understand the concept but also increase your speed and accuracy in proving triangle congruence. Here are some tips for effective practice:
- Time yourself to simulate test conditions.
- Review common mistakes and learn from them.
- Use software or apps designed for geometric proofs to check your work.
Through these sheets, you'll begin to see the patterns and commonalities in how triangles are proven to be congruent. This recognition is crucial for mastering geometry.
To wrap up, mastering triangle congruence proofs involves understanding the foundational postulates, practicing regularly, and knowing how to apply logical reasoning effectively. With the right approach and ample practice through these detailed practice sheets, you'll find triangle proofs becoming more straightforward and less daunting.
What are the main postulates for proving triangle congruence?
+
The main postulates for proving triangle congruence are SSS, SAS, ASA, AAS, and HL.
How can practice sheets help with learning triangle congruence proofs?

+
Practice sheets provide structured exercises to reinforce understanding, increase speed, and highlight common proof strategies.
Are there any tips for beginners starting with triangle congruence proofs?

+
Beginners should start with simpler proofs, use visual aids like diagrams, and focus on understanding one postulate at a time before combining multiple ones in a proof.



