Triangle Congruence Geometry: Ultimate Worksheet Guide
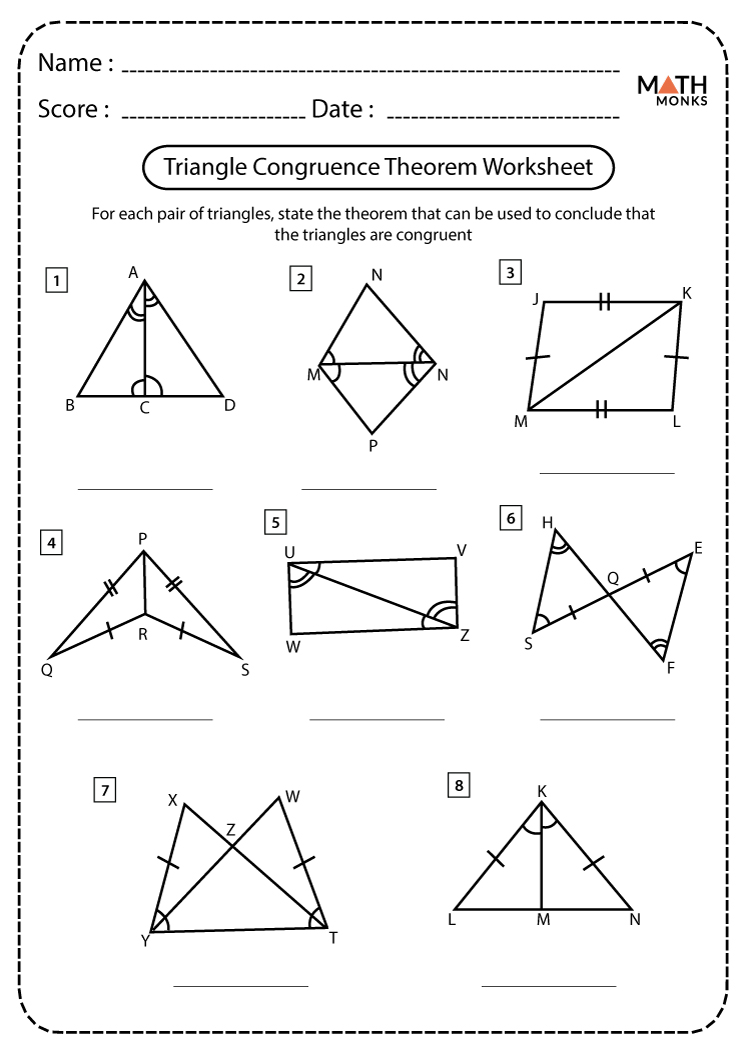
Triangle congruence is a fundamental concept in geometry that involves proving that two triangles have identical shapes and sizes. This guide aims to provide a detailed understanding of triangle congruence, how to identify congruent triangles, and offers practical worksheets for practice.
Criteria for Triangle Congruence

When proving that two triangles are congruent, we use several methods or criteria, each based on different sets of information:
- Side-Angle-Side (SAS): If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, the triangles are congruent.
- Angle-Side-Angle (ASA): If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, they are congruent.
- Side-Side-Side (SSS): When all three sides of one triangle are equal to all three sides of another, the triangles are congruent.
- Angle-Angle-Side (AAS): If two angles and a non-included side are equal, the triangles are congruent.
- Hypotenuse-Leg (HL): Specifically for right triangles, if the hypotenuse and one leg are equal, the triangles are congruent.
Proving Congruence

To prove congruence, follow these steps:
- Identify Known Information: Determine what angles or sides are known to be congruent.
- Choose the Congruence Criteria: Apply the appropriate method from the criteria listed above.
- Construct a Proof: Write down statements and reasons, linking each step to the known information or geometric properties.
⚠️ Note: For certain proofs, additional geometric properties or theorems might be necessary, like the vertical angle theorem or the alternate interior angles theorem.
Worksheet Guide

Here are some worksheet guides for students to practice triangle congruence:
Worksheet 1: Basics of Triangle Congruence

This worksheet focuses on identifying and marking congruent triangles:
- Provide several pairs of triangles with some marked sides or angles.
- Ask students to label the triangles, identify congruent parts, and name the congruence criteria (e.g., SAS, ASA).
Worksheet 2: Proving Congruence
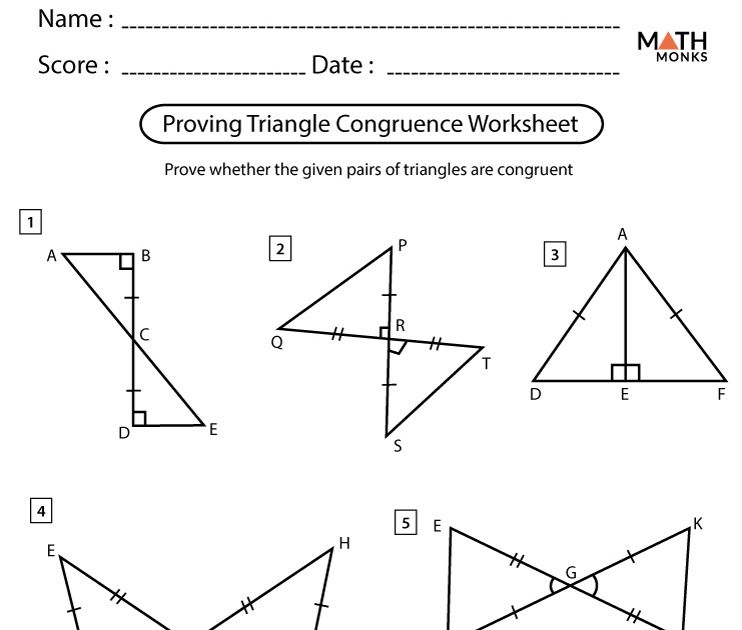
This worksheet involves:
- A series of exercises where students need to prove two triangles are congruent by using given information and writing out a logical proof.
| Problem | Given Information | Congruence Criteria |
|---|---|---|
| 1 | AB = PQ, AC = PR, ∠A = ∠P | ASA |
| 2 | XY = MN, ∠X = ∠M, ∠Y = ∠N | AAS |
| 3 | Side A = Side D, Side B = Side E, Angle between A and B = Angle between D and E | SAS |

🔧 Note: Encourage students to always write the correct symbols and labels when identifying congruent parts on their worksheet.
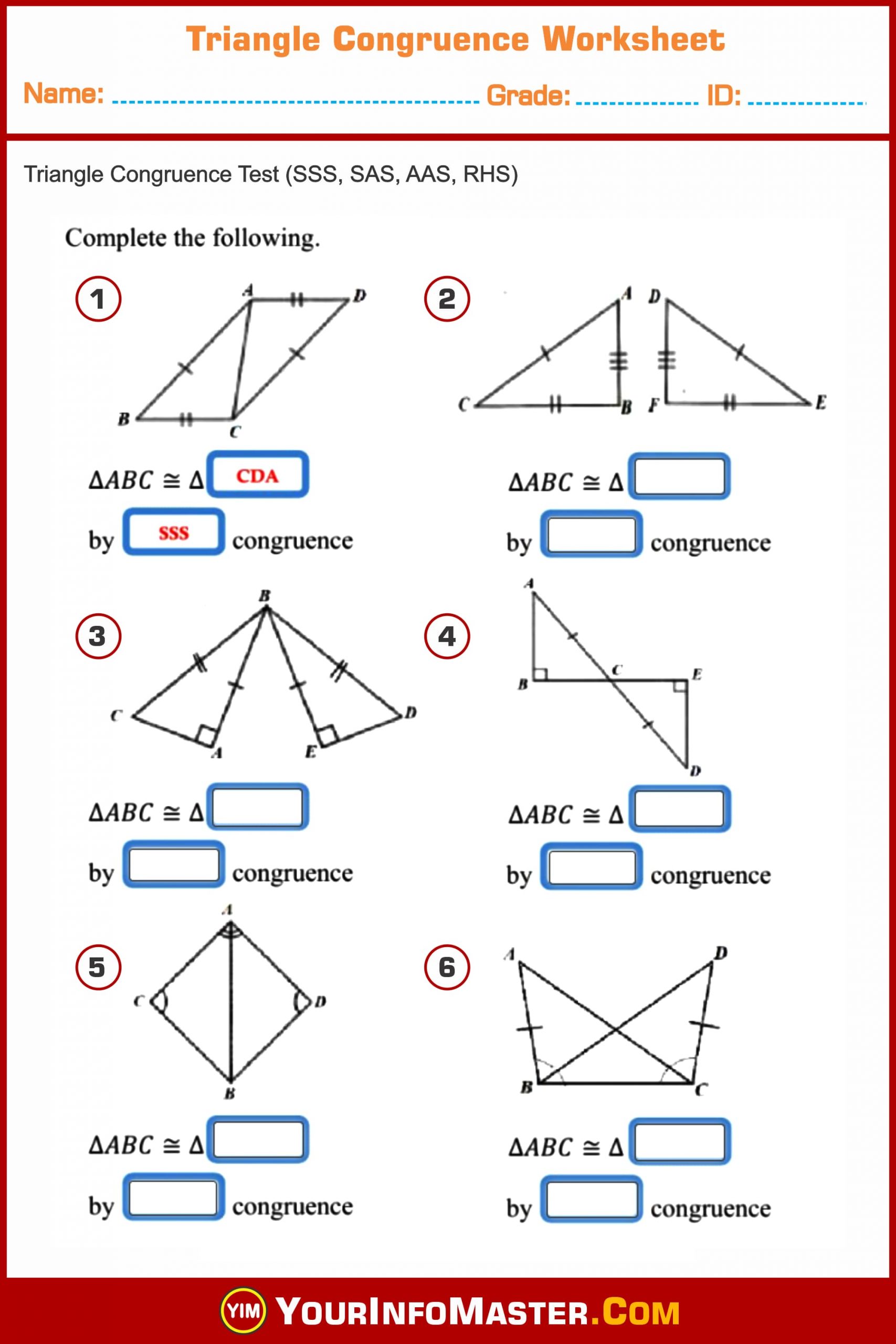
Worksheet 3: Mixed Congruence

This worksheet includes:
- Exercises where students must identify the congruence method and then use it to solve for missing angles or side lengths in congruent triangles.
Key Points to Remember

In mastering triangle congruence, keep these points in mind:
- Congruence is not the same as similarity; congruent triangles are also similar, but similar triangles might not be congruent.
- When dealing with proofs, organize your statements and reasons clearly to make your proof straightforward and understandable.
- Practice identifying which congruence criteria to use by closely examining the given information in the problems.
Overall, understanding triangle congruence not only helps in solving geometric problems but also lays a foundation for advanced mathematical concepts. By regularly practicing with worksheets and engaging with the concept through diverse problems, students can develop a strong grasp of how triangles can be proven congruent, thereby enhancing their geometric skills.
What is the difference between congruence and similarity?

+
Congruent triangles are identical in shape and size, while similar triangles have the same shape but not necessarily the same size. Congruence includes similarity but requires equal corresponding sides and angles.
Can you use HL for any triangle to prove congruence?
+
No, the HL (Hypotenuse-Leg) criterion applies only to right triangles. For other triangles, you would use criteria like SSS, SAS, or ASA.
Why isn’t AA (Angle-Angle) a valid method for proving triangle congruence?

+
The AA criterion only tells us that the triangles are similar, not congruent. For congruence, we need more than just angles; sides must also match in length.
How can I practice triangle congruence?

+
Use worksheets or textbooks with dedicated sections on triangle congruence, participate in geometry problem-solving clubs, or find online resources like GeoGebra for interactive practice.



