5 Essential Transformations of Parent Functions Worksheet Tips
Mastering parent functions is crucial in mathematics, especially when you're delving into algebra and calculus. Parent functions are the simplest forms of common functions, providing a foundation upon which transformations are built. Here, we'll explore five essential tips to help students effectively use parent functions worksheets, which are indispensable tools for understanding function transformations. By mastering these tips, you'll enhance your comprehension of how functions can be manipulated and applied in various scenarios.
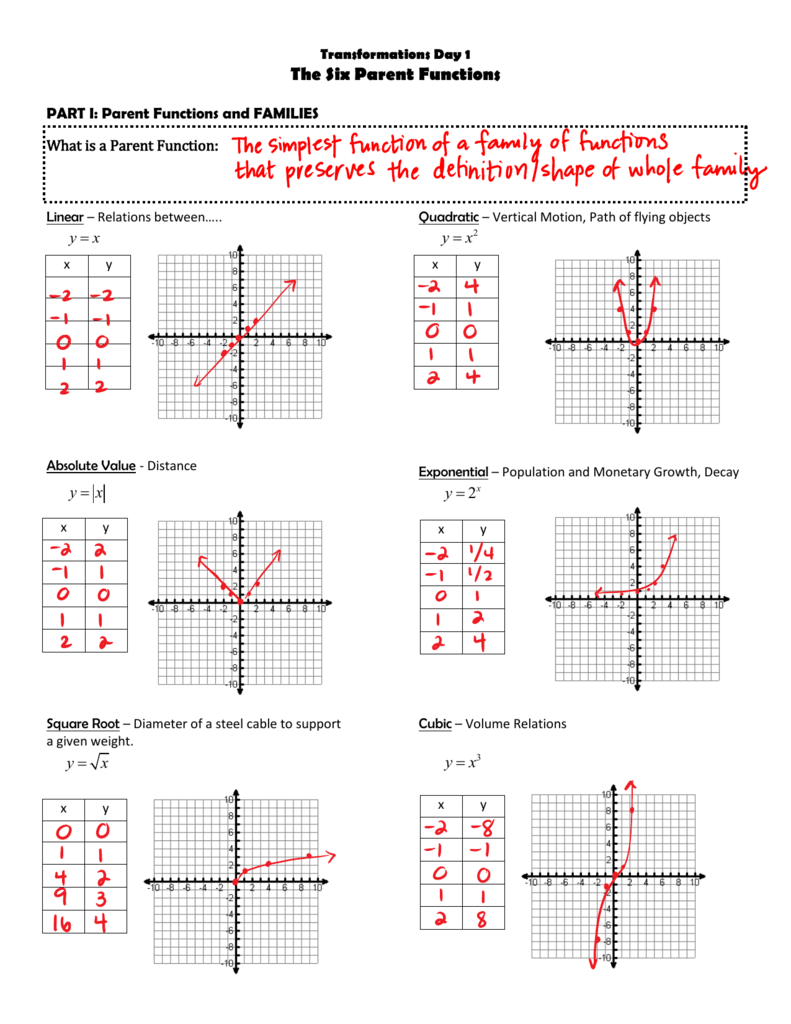
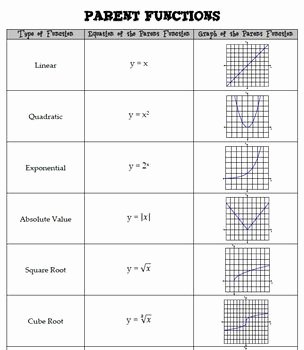
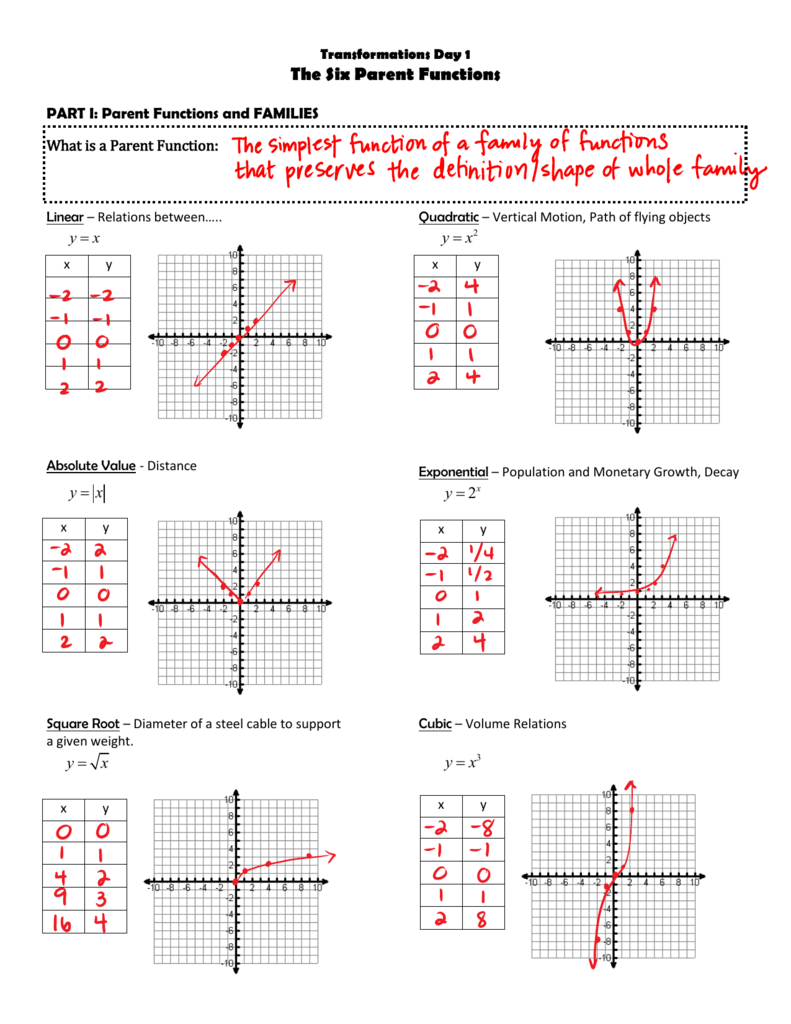
Understanding the Basics of Parent Functions

Before diving into transformations, it's pivotal to understand what parent functions are:
- Definition: A parent function is the simplest form of a function in a family of functions, serving as a building block for other functions within that family.
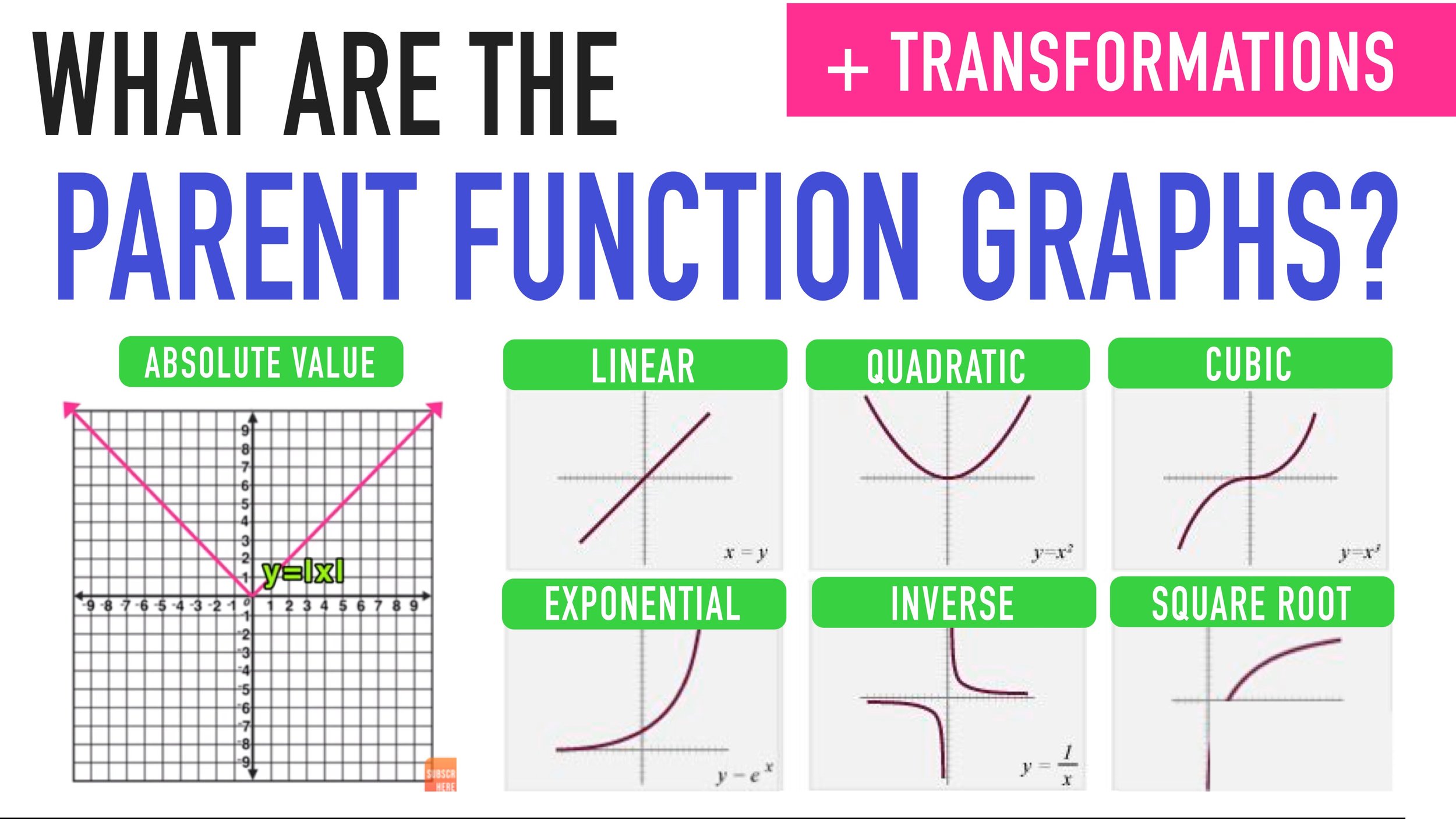
- Examples:
- Linear Function: f(x) = x
- Quadratic Function: f(x) = x^2
- Exponential Function: f(x) = 2^x
📚 Note: Parent functions are not limited to these examples; they include trigonometric, logarithmic, and other types of functions.
Identifying Key Characteristics
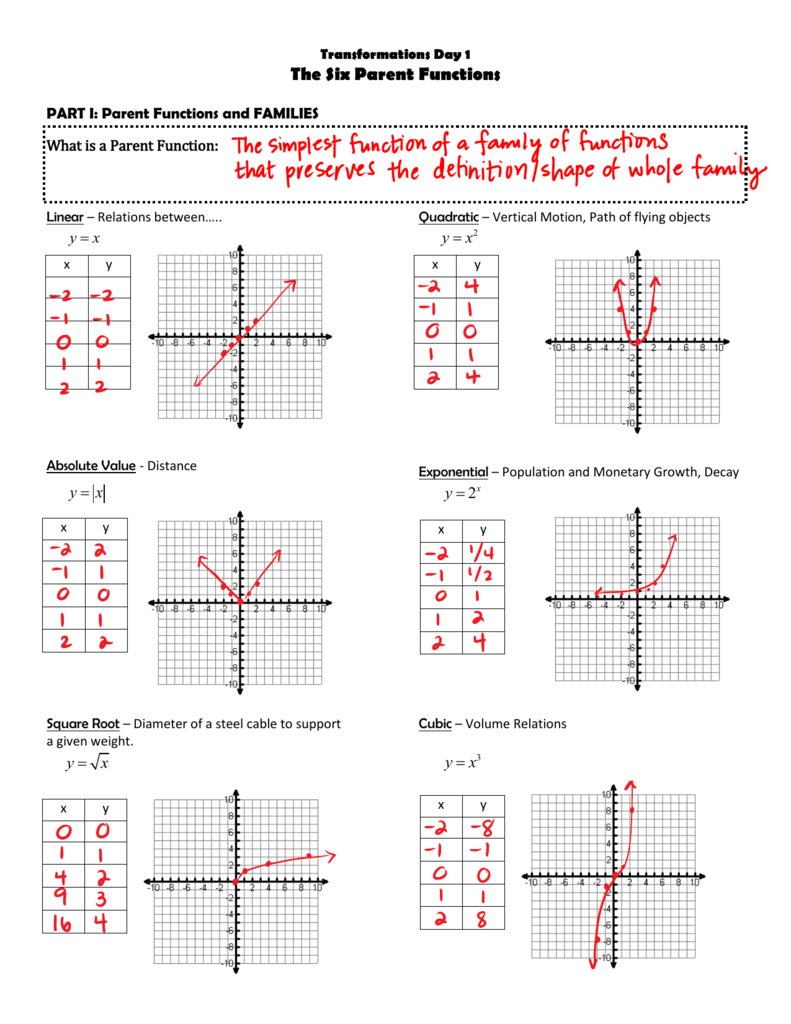
Each parent function has specific characteristics:
- Domain: All real numbers for most functions unless otherwise specified.
- Range: Varies based on the function; for instance, f(x) = x^2 has a range of [0, \infty) .
- Intercepts: The point where the function crosses the axes (x-intercept and y-intercept).
Recognizing Transformations

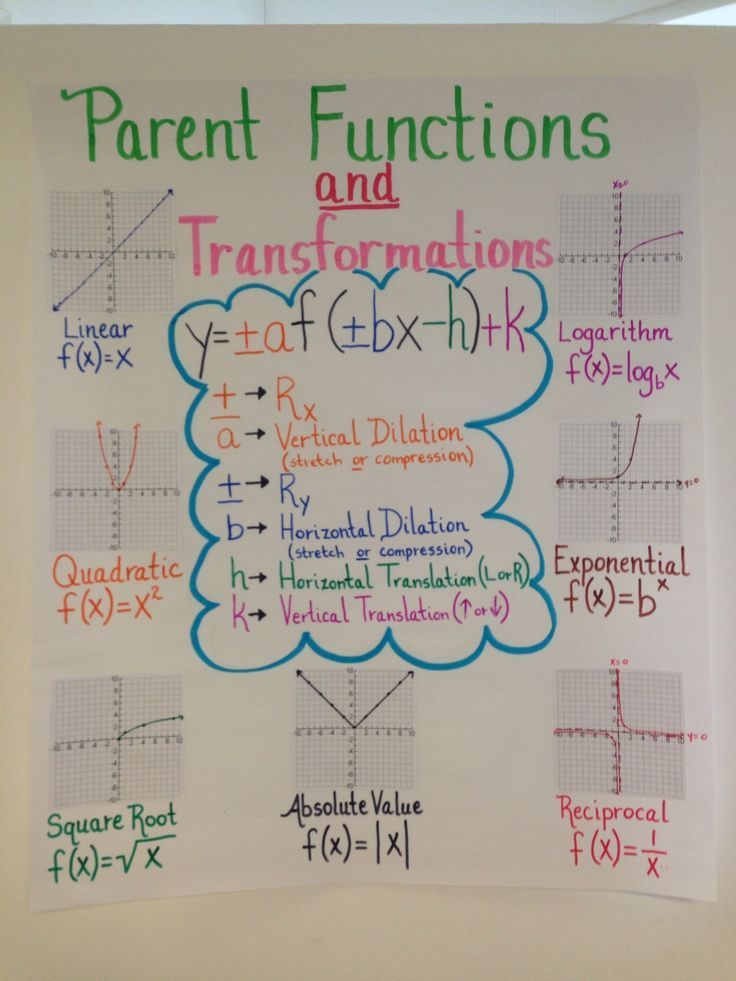
Transformations of parent functions involve four key operations:
1. Translation
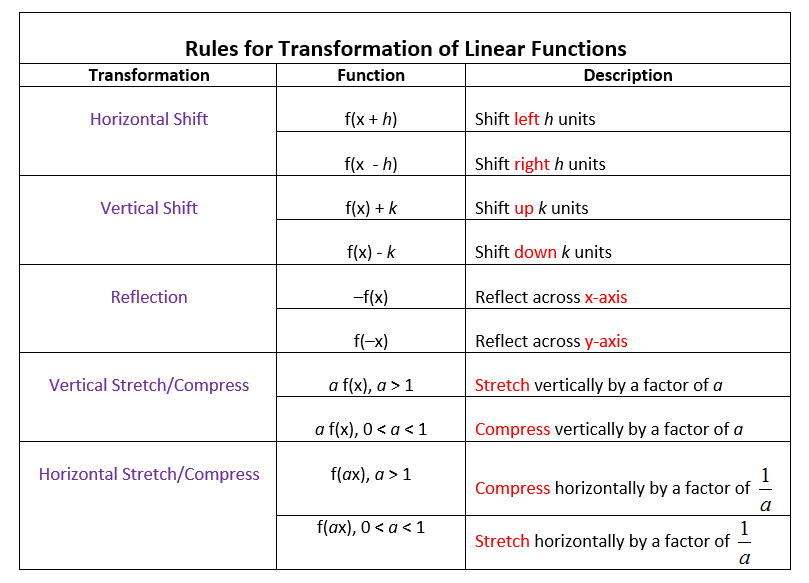
This involves moving the function either horizontally or vertically:
- Horizontal Translation: Adding or subtracting inside the function. For example, f(x+3) shifts f(x) left by 3 units.
- Vertical Translation: Adding or subtracting outside the function. For example, f(x) + 3 shifts f(x) up by 3 units.
2. Scaling
Scaling changes the size or height of the function:
- Vertical Scaling: Multiplying by a constant outside the function. For example, 2f(x) doubles the height of f(x) .
- Horizontal Scaling: Multiplying inside the function, often affecting the stretch or compression. For instance, f(2x) compresses horizontally.
3. Reflection
Reflecting the function over an axis:
- Reflection Over the X-Axis: -f(x) .
- Reflection Over the Y-Axis: f(-x) .
4. Combining Transformations

Multiple transformations can be applied together:
- When combining, order matters: vertical transformations are typically applied last.
🔍 Note: To determine the order of transformations, consider the effects on the function one at a time.
Using Worksheets Effectively
Worksheets serve as practical tools for practicing transformation:
- Graphing: Sketch both the original function and the transformed function on the same axes.
- Step-by-Step Solution: Break down each transformation and explain how it affects the parent function.
- Table of Values: Use tables to track how transformation changes the function's values.
| Transformation | Effect on f(x) |
|---|---|
| Vertical Stretch/Compression | a * f(x) |
| Horizontal Stretch/Compression | f(b * x) |
| Reflection over X-axis | -f(x) |
| Reflection over Y-axis | f(-x) |
| Vertical Translation | f(x) + k |
| Horizontal Translation | f(x + h) |
By systematically approaching transformations, students can visualize and internalize how each change modifies the original function.
Practice and Application
Utilize parent functions worksheets to:
- Create your own transformations for better understanding.
- Identify and apply multiple transformations in complex scenarios.
- Solve real-world problems by applying function transformations.
✨ Note: Real-world applications often require not just one transformation but a combination tailored to the situation.
Ultimately, mastering parent functions and their transformations is not just about understanding algebra or calculus but about comprehending how models in mathematics can be altered to reflect changes in our environment or systems. By using these five tips effectively, you're equipped with a toolkit to not only solve mathematical problems but also to think critically and creatively in any discipline where functions play a role. Whether it's in graphing data sets, designing algorithms, or even understanding physical phenomena, the ability to manipulate parent functions empowers you to tackle a wide array of challenges with mathematical finesse.
What is a parent function?

+
A parent function is the simplest form of a function within a family of functions. It serves as the basic model which all other functions in that family are derived from through transformations.
How do I determine the type of transformation from a worksheet?

+
Identify keywords or symbols in the function that indicate specific transformations. For example, adding or subtracting outside the function indicates vertical translation, while inside denotes horizontal translation. Look for multiplication or division for scaling, and negative signs for reflections.
Why are parent functions important in math?

+
Parent functions serve as the foundation for understanding how functions behave under various transformations. They help in visualizing the effects of these transformations, making complex algebraic or calculus problems more manageable and intuitive.



