Master Slope Calculations with Our Line Worksheet Guide

The ability to calculate slopes and interpret linear relationships is a critical part of understanding algebra and geometry, both of which are pivotal in the learning of higher mathematics. As you embark on this mathematical journey, mastering slope calculations will enhance your skills in graphing lines and interpreting their properties. This comprehensive guide will delve into the principles of slope calculations, provide practical examples, and assist in better comprehension through the use of line worksheets. Here, we'll explore everything from the basics to advanced concepts, ensuring a robust grasp of the topic.
Understanding Slope: The Fundamental Concepts
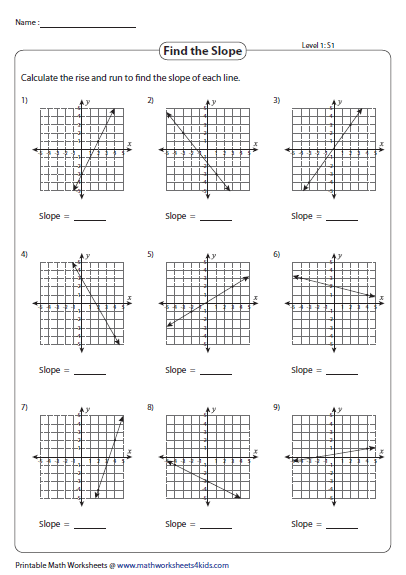
Slope is a measure of the steepness of a line, offering insight into how the line is inclining or declining. It’s calculated as the ratio of the vertical change (the ‘rise’) to the horizontal change (the ‘run’). This can be expressed mathematically as:
[ \text{slope} (m) = \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x1} ]
- Rise refers to the difference in y-coordinates.
- Run refers to the difference in x-coordinates.
📊 Note: The terms 'rise' and 'run' are often used to explain how a line changes as one moves from one point to another. In everyday situations, 'rise' might represent elevation change or price change, while 'run' could mean distance traveled or time passed.
Types of Slopes

Lines can exhibit various types of slopes which give us an immediate idea of their direction:
- Positive Slope: As ( x ) increases, ( y ) increases, creating a line that moves upwards from left to right.
- Negative Slope: As ( x ) increases, ( y ) decreases, resulting in a line that moves downward from left to right.
- Zero Slope: The line is horizontal; there’s no rise, only run.
- Undefined Slope: The line is vertical; there’s no run, only rise.
To visualize these, a line worksheet can be immensely helpful in plotting different lines and observing their slopes.
Calculating Slope Using Coordinates

When given two points on a line, you can calculate the slope directly using the slope formula mentioned above:
Example: With coordinates (3, 2) and (5, 6):
[ m = \frac{6 - 2}{5 - 3} = \frac{4}{2} = 2 ]
This indicates that for every two units you move to the right, you move four units up, leading to a slope of 2.
Slope-Intercept Form
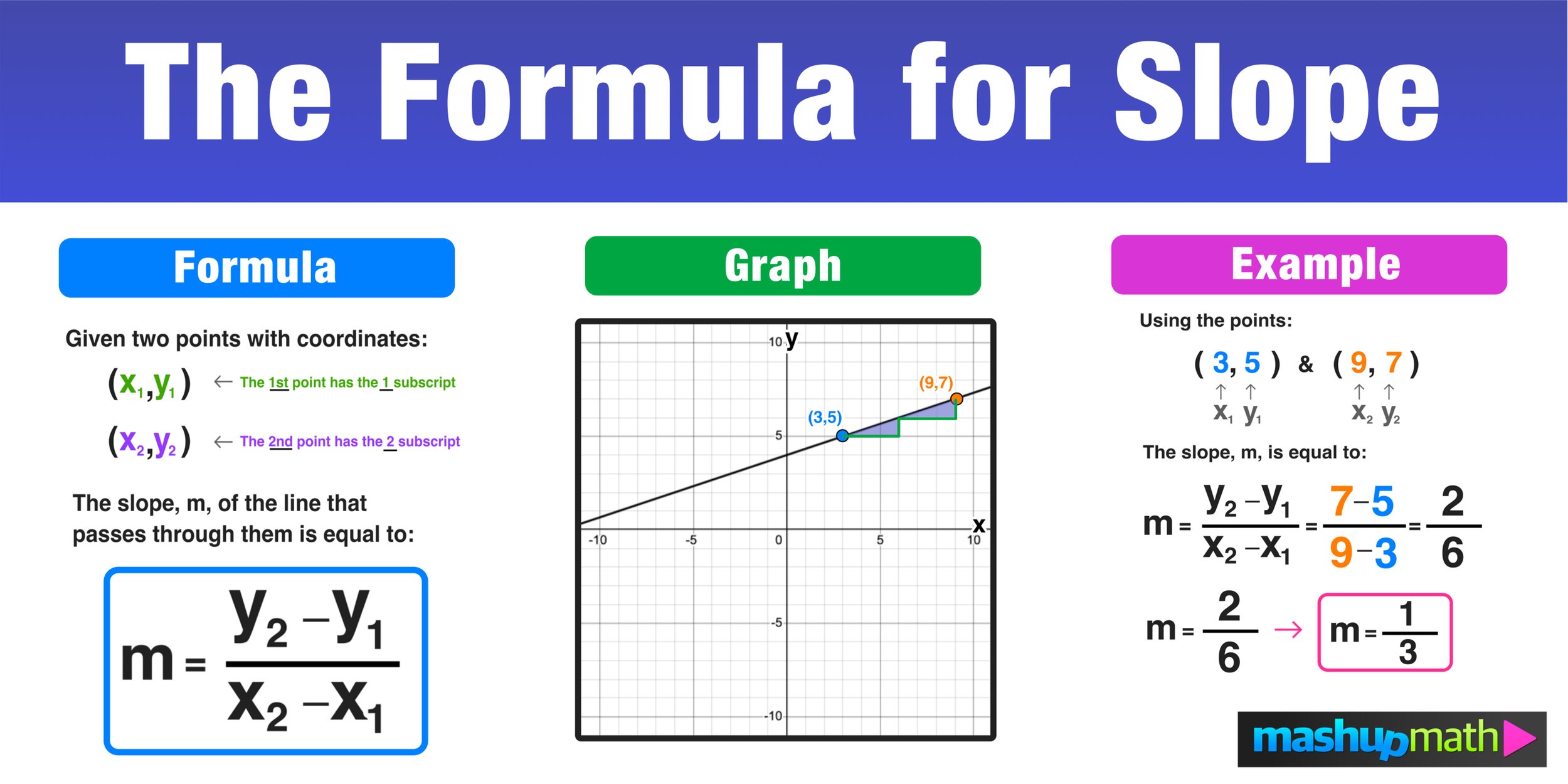
In addition to calculating slope using coordinates, the slope-intercept form of a line’s equation, ( y = mx + b ), where ( m ) is the slope and ( b ) is the y-intercept, is extremely useful. Here are some tips on working with this form:
- Identify the slope ( m ) directly from the equation.
- The y-intercept ( b ) is where the line crosses the y-axis, which is often marked as point (0, b).
- Plotting points using the intercept allows for a quicker visualization of the line.
A worksheet that focuses on converting between different forms of a line's equation can significantly improve one's ability to manipulate and understand lines.
✨ Note: The slope-intercept form is a linear equation, but not all equations of a line are written in this form. Some might be in standard form, point-slope form, or even an intercept form, so being versatile in converting between forms is a valuable skill.
Practical Examples with Line Worksheets

Here are some practical examples to solidify your understanding:
Example 1: Plotting Points and Finding Slope

Given points (1, 2) and (4, 7), calculate the slope and plot the line:
- Calculate the slope: ( m = \frac{7 - 2}{4 - 1} = \frac{5}{3} )
- Plot these points on a graph.
- Draw a line passing through these points.
Example 2: Finding the Equation from the Slope

If you know a line has a slope of 4 and passes through (0, 3), write its equation in slope-intercept form:
- The y-intercept ( b ) is 3.
- Using the slope ( m = 4 ), the equation becomes ( y = 4x + 3 ).
These examples would be well-suited for inclusion in a line worksheet where students can practice these steps:
| Exercise | Description |
|---|---|
| Ex. 1 | Plot two given points and find the slope. |
| Ex. 2 | Determine the equation of the line given its slope and y-intercept. |

🔔 Note: Creating or utilizing worksheets can enhance your understanding through repetition and immediate application of the concept. They often provide instant feedback on your mastery of the material.
The Real-World Applications of Slope
The concept of slope extends beyond the classroom and into real-world applications:
- Engineering: Calculating slopes for roads, railways, or roller coaster tracks to ensure smooth transitions.
- Architecture: Slopes are used in designing buildings, ramps, and stairs for safety and accessibility.
- Economics: Analyzing cost-benefit ratios, production lines, or demand and supply curves.
- Physics: Studying velocity, acceleration, and the forces acting on objects.
Incorporating these practical applications into your learning can make the subject more relatable and interesting.
Conclusion

Mastery of slope calculations is not just about solving problems but about understanding the underlying principles that govern the behavior of lines. By utilizing line worksheets, you can actively practice plotting points, calculating slopes, and interpreting lines, all of which are essential for a comprehensive understanding of algebra and geometry. Through the examples provided and the real-world applications, you can see how this knowledge connects to everyday situations, making the learning process more engaging. Remember, proficiency in these areas builds a solid foundation for tackling more complex mathematical concepts in the future.
Why is slope important in mathematics?

+
Slope is essential in mathematics because it describes how the graph of a function changes over the x-axis. It helps in understanding rates of change, linear equations, and forms the basis for differentiation in calculus.
Can slope be zero or undefined?
+
Yes, slope can be zero when a line is horizontal (no rise) and undefined when a line is vertical (no run). These are special cases that represent flat surfaces and vertical walls, respectively.
How can I use line worksheets for better learning?

+
Line worksheets provide practical exercises to plot points, find slopes, and construct line equations. They reinforce your understanding of slope and its various forms, making the theory more tangible through active learning.
What are some common mistakes when calculating slopes?

+
Common mistakes include: mixing up the coordinates, using the wrong formula, or miscalculating the rise and run. Always double-check your signs (positive or negative) and ensure your coordinates are correctly placed in the formula.