Tis the Season for Slope Formula Answers Keyed

The holiday season often brings thoughts of decorations, feasts, and joy, but for students in the midst of holiday break, it's not just all fun and games. Mathematics, particularly algebra, remains a fundamental part of their education. Among the key concepts being mastered over this break is the slope formula, a critical component of understanding linear equations. This blog delves into slope formula answers key, providing a thorough explanation to help students not just survive but thrive in their algebra classes. Here's everything you need to know about the slope formula to conquer your next math quiz or test during this festive season.
Understanding the Slope Formula

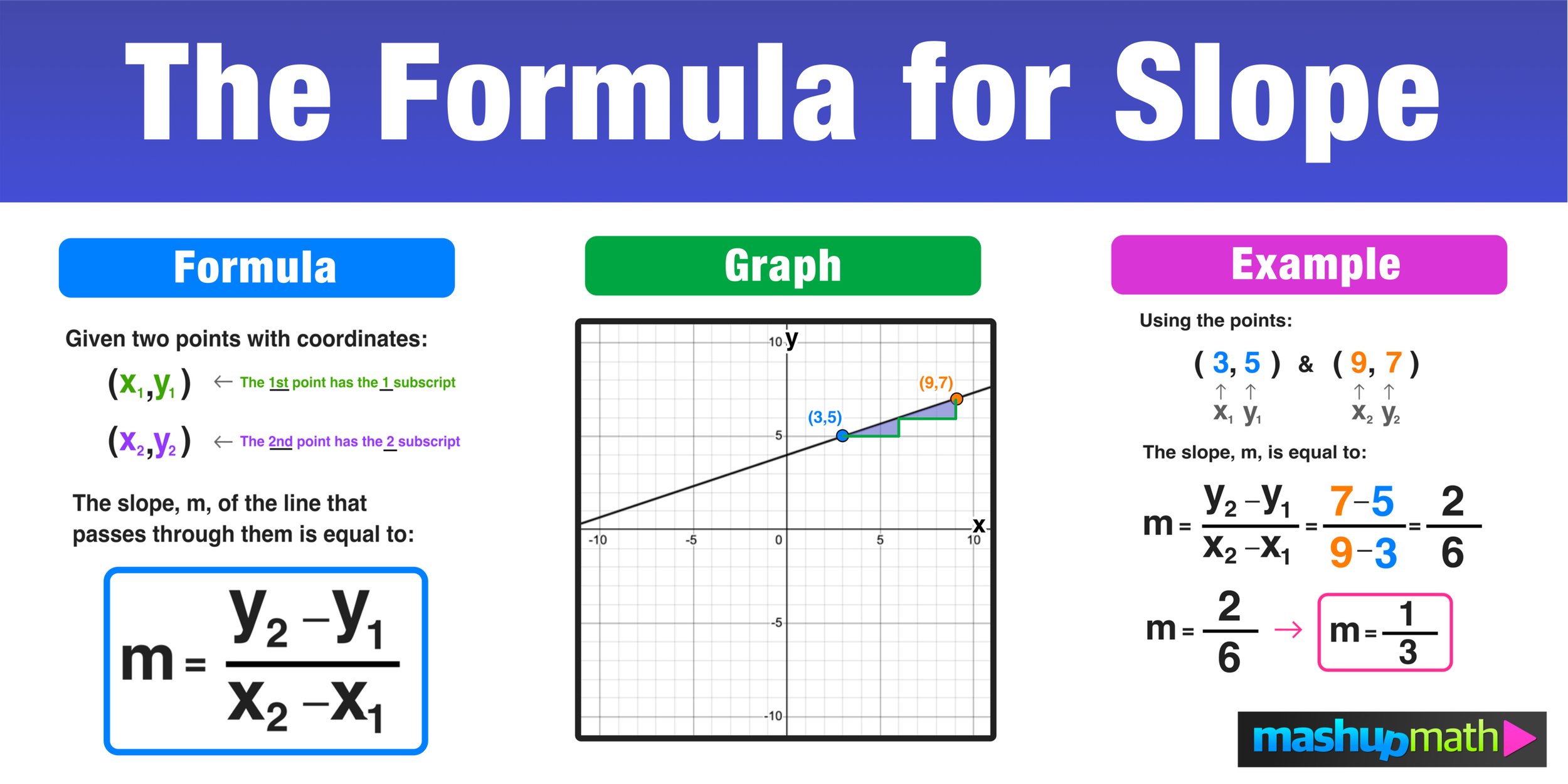
The slope of a line is a measure of its steepness, how much the line inclines or declines. The formula for calculating the slope between two points ((x_1, y_1)) and ((x_2, y_2)) is:
[ m = \frac{{y_2 - y_1}}{{x_2 - x_1}} ]
Here are the key components of this formula:
- m: This represents the slope of the line.
- y2 - y1: This is the “rise,” or the vertical change.
- x2 - x1: This is the “run,” or the horizontal change.
Real-Life Applications

Slope isn’t just an abstract concept; it has real-world applications. From calculating the gradient of a road to understanding rates of change in physics or economics, here are some examples:
- Road Construction: Engineers need to design roads with specific slopes to ensure safety and proper drainage.
- Roof Pitch: Architects use slope to determine how steep a roof should be.
- Economic Trends: Economists study the slope of demand and supply curves to understand market dynamics.
Practical Examples of the Slope Formula

Let’s take a practical look at how the slope formula is applied:
Example 1: Finding Slope Between Two Points

Consider two points ((2, 3)) and ((6, 11)). Plugging these values into our slope formula gives:
[ m = \frac{{11 - 3}}{{6 - 2}} = \frac{8}{4} = 2 ]
This line has a slope of 2, indicating that for every 2 units you move up the y-axis, you move 1 unit along the x-axis.
Example 2: Horizontal and Vertical Lines

If one point is ((4, 5)) and the other is ((4, -3)), the line is vertical:
[ m = \frac{{-3 - 5}}{{4 - 4}} = \frac{{-8}}{0} = undefined ]
Vertical lines do not have a defined slope, while horizontal lines have a slope of 0. Understanding these special cases is crucial.
Common Mistakes and Misconceptions

Students often make mistakes when calculating slope. Here are some common pitfalls:
- Order of Subtraction: Subtracting the y-values and x-values in the wrong order.
- Handling Zero Differences: Misunderstanding the implications of when either the rise or run is zero.
- Not Reducing Fractions: Not simplifying the resulting fraction to its simplest form.
📝 Note: When dividing by zero, remember that this yields an undefined slope, leading to vertical lines.
Visualizing Slope with Graphs

Graphing lines and visualizing the slope can solidify understanding. Here’s how:
- Plot the two points on the coordinate plane.
- Calculate the slope using the formula.
- Draw a line through the points, ensuring it follows the calculated slope.
An image here can help illustrate this process, but for now, imagine a line with a slope of 2 passing through points ((2, 3)) and ((6, 11)).
How to Master Slope Formula for Exams

Mastering the slope formula involves practice, understanding key concepts, and recognizing common errors. Here are some tips:
- Practice Regularly: Use online tools or textbooks to get diverse examples.
- Understand the Geometry: Visualize the line in your mind before using the formula.
- Review Special Cases: Be ready for lines with zero or undefined slopes.
⚠️ Note: In some cases, especially with vertical lines, understanding the concept of direction is key, not just the numeric value of the slope.
Conclusion

The slope formula is a foundational part of algebra, with its applications reaching far beyond the classroom into practical aspects of life. This blog has not only provided a slope formula answers key but also offered insights into its real-world uses, common errors, and strategies for mastering it. With this comprehensive guide, you’re now better prepared to tackle algebra problems involving slope, ensuring that this holiday season is not just about relaxation but also about intellectual growth and preparation for upcoming academic challenges.
Why is slope important in algebra?

+
Slope is crucial in algebra because it defines the rate of change of one variable with respect to another, essential for understanding linear functions, and predicting future values in linear relationships.
How do you know if a slope is positive or negative?

+
The slope is positive if, when moving from left to right on the coordinate plane, the line goes up. Conversely, it’s negative if the line goes down. This directionality indicates whether the dependent variable increases or decreases with the independent variable.
What are the implications of a zero slope?
+
A zero slope indicates a horizontal line, where there is no change in the y-values for any change in the x-values. This implies that the variable on the y-axis (often the dependent variable) is constant, irrespective of the changes in the variable on the x-axis (often the independent variable).



