5 Key Strategies for Solving Systems of Equations

The Importance of Systems of Equations in Problem Solving

In the realm of mathematics, systems of equations are not just academic exercises; they are essential tools for modeling and solving real-world problems. From optimizing financial portfolios to balancing chemical reactions, understanding how to solve systems of equations provides foundational skills for numerous applications. Here, we’ll explore five key strategies to tackle these systems effectively.
Method 1: Substitution Method

Substitution is often the first method taught in algebra due to its straightforward nature:
- Isolate a variable: In one of the equations, solve for one variable in terms of the other.
- Substitute: Replace the isolated variable in the other equation with the expression obtained.
- Solve for the remaining variable: Now that one equation contains only one variable, solve it.
- Substitute back: Once the second variable is found, substitute it back into the expression to solve for the other variable.
💡 Note: The substitution method is particularly effective when one of the equations already has a variable isolated or can be easily solved for a variable.
Method 2: Elimination Method

When variables cannot be isolated conveniently, the elimination method can provide a solution:
- Add or subtract equations: Adjust the equations so that one variable can be eliminated when added or subtracted.
- Eliminate one variable: Perform the addition or subtraction.
- Solve for the remaining variable: With one variable gone, solve the resulting equation for the other variable.
- Back substitution: Substitute the value found into either of the original equations to find the value of the eliminated variable.
This method leverages the linear nature of the equations to cancel out variables, making it particularly useful when the coefficients are simple multiples of each other.

Method 3: Graphical Method

The graphical method transforms algebraic problems into visual ones:
- Graph each equation: Plot each line on a coordinate plane.
- Find the intersection: The point where the lines cross is the solution to the system.
- Interpret results: Solutions might be exact or approximate, depending on the precision of the graph.
While less precise than algebraic methods for numerical solutions, this method can provide insights into the behavior of the system, especially for systems with no or infinite solutions.
Method 4: Matrix Method (Gaussian Elimination)

For more complex systems with three or more variables, matrix methods can be advantageous:
- Represent equations as matrices: Each equation becomes a row in an augmented matrix.
- Perform row operations: Use operations like adding multiples of one row to another to zero out elements above the leading 1 in each column.
- Reduce to row echelon form: Continue until the matrix is in a form where back substitution can easily find the solution.
📝 Note: Gaussian elimination provides a systematic approach to solving systems of linear equations, especially when dealing with systems that are difficult to solve through substitution or elimination due to complexity or size.
| Operation | Description |
|---|---|
| Row Multiplication | Multiply an entire row by a scalar. |
| Row Addition | Add a multiple of one row to another. |
| Row Exchange | Swap two rows. |

Method 5: Cramer’s Rule

Cramer’s Rule offers an elegant way to solve systems through determinants:
- Set up the main determinant: Use the coefficient matrix to form the determinant.
- Compute the determinant: Calculate this value.
- Set up determinants for variables: Replace the respective column with the constants from the right-hand side of the equations.
- Divide: Each variable’s value is the ratio of its respective determinant to the main determinant.
🔍 Note: Cramer's Rule is particularly useful for systems of equations where the determinant is not zero and provides direct insight into the solution without iterative processes.
In closing, systems of equations are not just a classroom exercise but a fundamental mathematical technique with real-world applications. Each method for solving these systems comes with its advantages:
- The Substitution method simplifies problems when one variable can be easily isolated.
- Elimination works well when the coefficients allow for easy elimination of variables.
- Graphical methods offer a visual interpretation, valuable for systems with special solutions.
- Matrix methods, like Gaussian Elimination, handle complexity and larger systems with ease.
- Cramer’s Rule gives a direct solution for systems where determinants are manageable.
By mastering these strategies, you equip yourself with versatile tools to tackle not only academic but also practical problems involving multiple variables and relationships.
When should I use substitution instead of elimination?

+
Use substitution when one of the equations already has a variable isolated or when you can easily solve one variable in terms of another. This method simplifies complex algebraic manipulations, making it ideal for systems where one equation has a straightforward variable isolation.
What are the limitations of the graphical method?

+
The graphical method is less precise, particularly for large numbers or when exact numerical values are needed. It’s also time-consuming for systems with many variables or when precise intersection points are difficult to read off the graph.
How do I know if a system of equations has no solution?
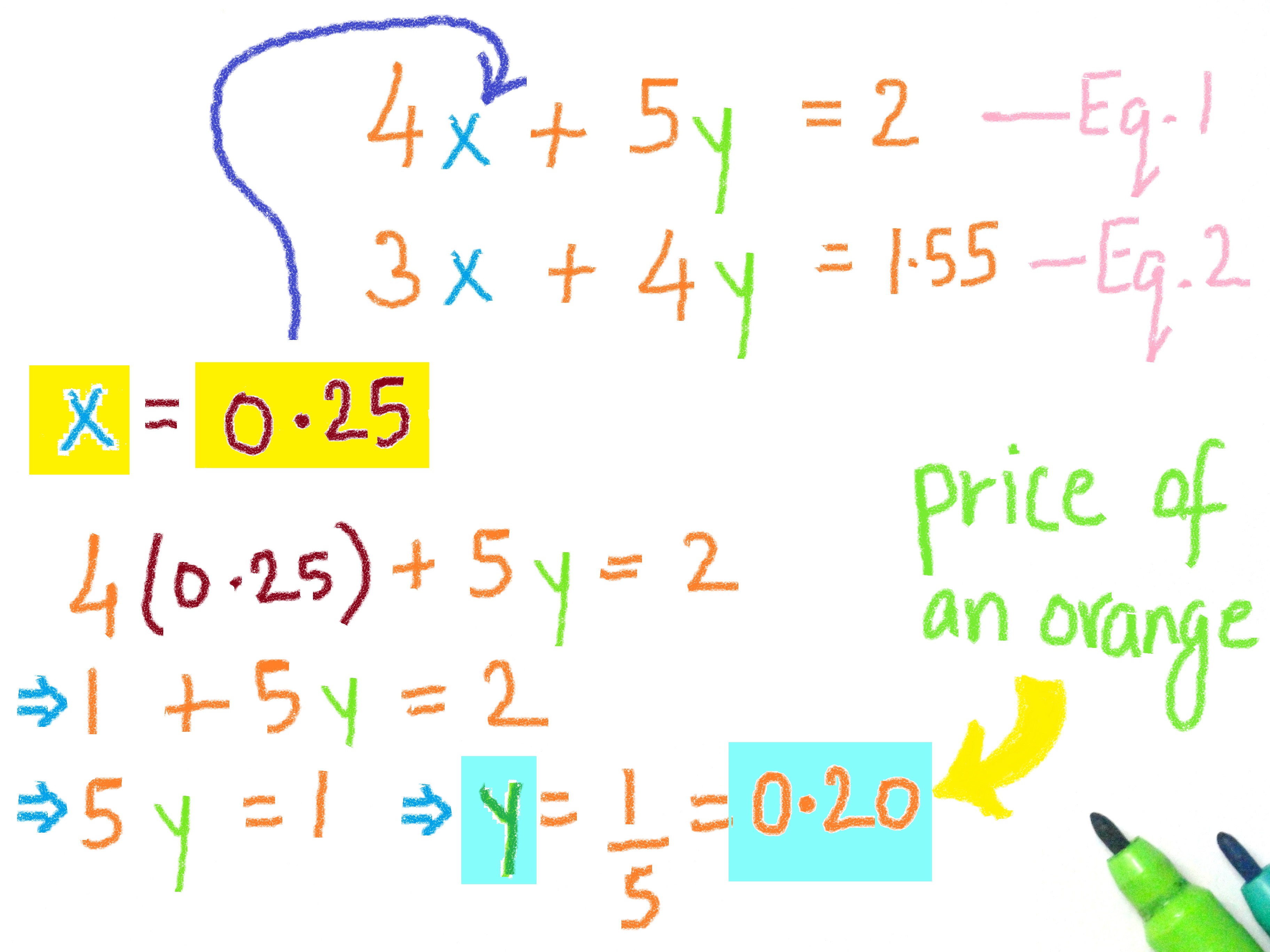
+
A system of equations has no solution if the lines representing the equations are parallel, which means they never intersect. Algebraically, this situation often results in a contradiction like 0 = 1 when solving the system.



