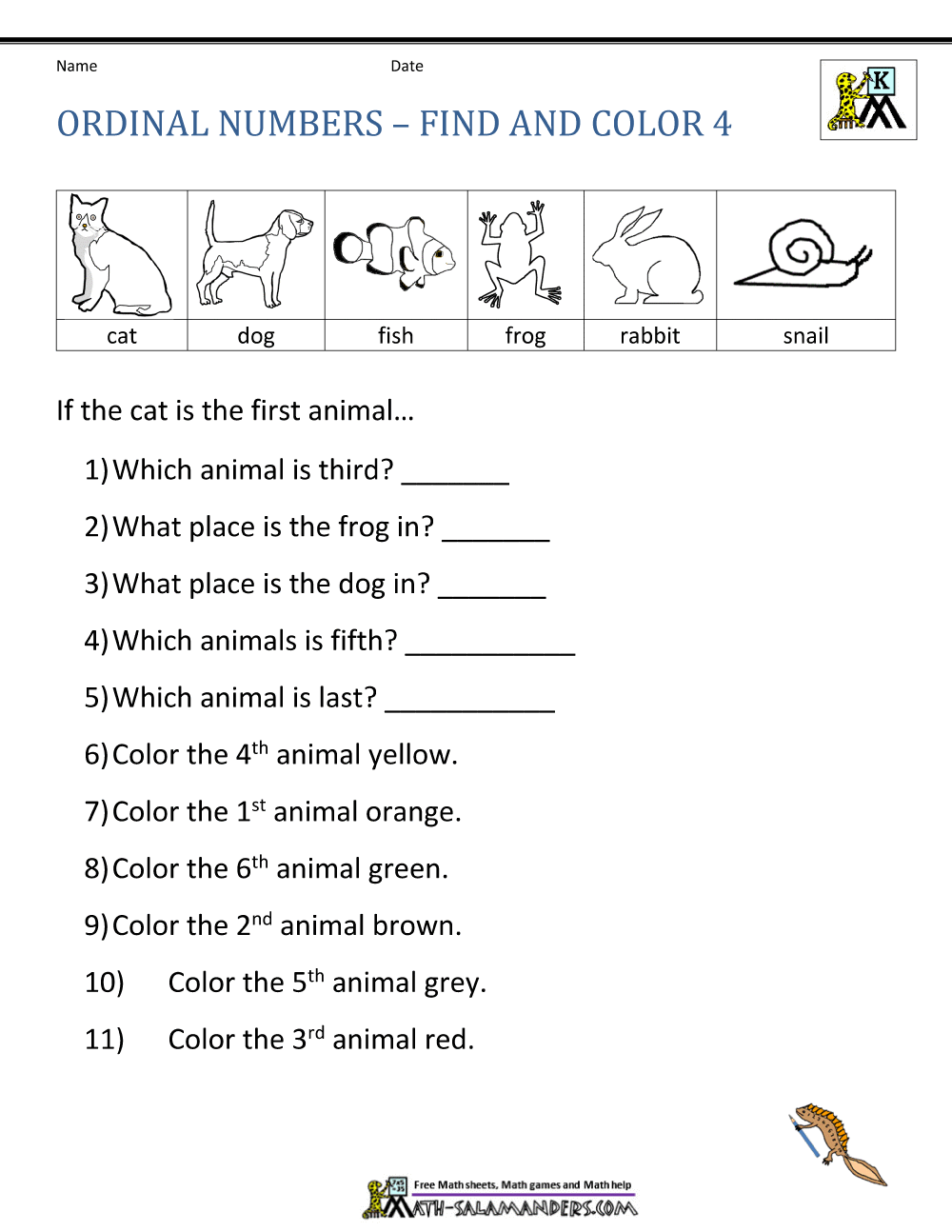
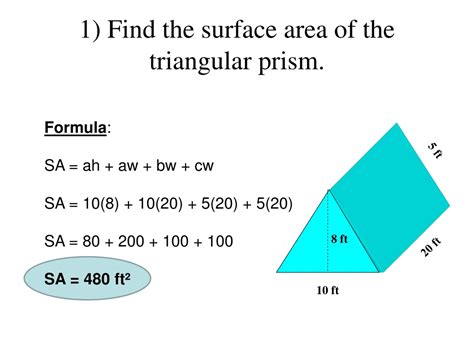
5 Ways to Calculate Triangular Prism Surface Area

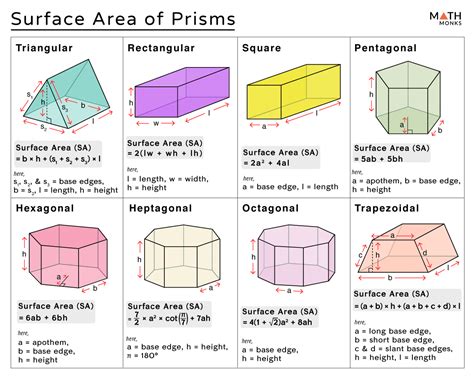
Understanding Triangular Prism Surface Area
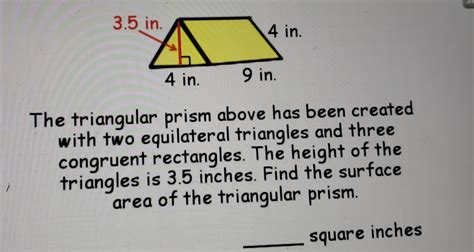
Calculating the surface area of a triangular prism is a fundamental concept in geometry and mathematics. A triangular prism is a three-dimensional shape with two identical triangular faces and three rectangular faces. The surface area of a triangular prism can be calculated using different formulas, depending on the information available. In this article, we will explore five ways to calculate the surface area of a triangular prism.
Method 1: Using the Formula SA = 2lw + 3lh
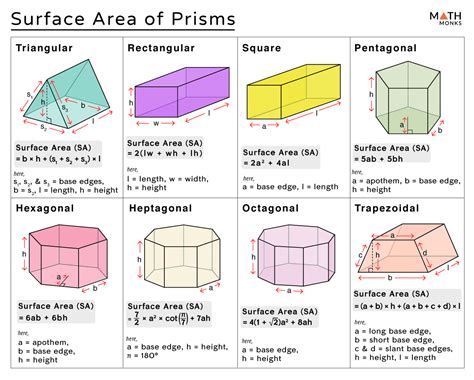
One of the most common formulas for calculating the surface area of a triangular prism is SA = 2lw + 3lh, where:
- SA is the surface area of the prism
- l is the length of the prism
- w is the width of the prism
- h is the height of the prism
This formula is useful when you know the length, width, and height of the prism.
📝 Note: This formula assumes that the two triangular faces are identical and that the three rectangular faces are identical.
Method 2: Using the Formula SA = 2A + Ph
Another way to calculate the surface area of a triangular prism is by using the formula SA = 2A + Ph, where:
- SA is the surface area of the prism
- A is the area of the triangular base
- P is the perimeter of the triangular base
- h is the height of the prism
This formula is useful when you know the area of the triangular base and the perimeter of the triangular base.
Method 3: Using the Formula SA = lw + 2l√(h^2 + (w/2)^2) + 2w√(h^2 + (l/2)^2)
This formula is a more complex way of calculating the surface area of a triangular prism. It is useful when you know the length, width, and height of the prism.
📝 Note: This formula uses the Pythagorean theorem to calculate the length of the rectangular faces.
Method 4: Using the Formula SA = 2lw + l√(h^2 + w^2) + w√(h^2 + l^2)
This formula is another way of calculating the surface area of a triangular prism using the length, width, and height of the prism.
📝 Note: This formula is similar to Method 3, but it uses a different combination of the Pythagorean theorem.
Method 5: Using the Formula SA = 2A + 3lw
This formula is a simpler way of calculating the surface area of a triangular prism. It is useful when you know the area of the triangular base and the length and width of the prism.
📝 Note: This formula assumes that the two triangular faces are identical and that the three rectangular faces are identical.
Example Problem
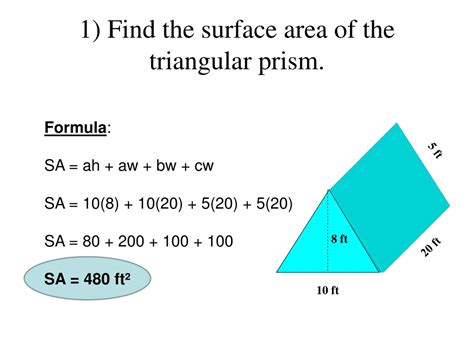
Find the surface area of a triangular prism with a length of 6 cm, a width of 4 cm, and a height of 3 cm.
| Method | Formula | Surface Area |
|---|---|---|
| Method 1 | SA = 2lw + 3lh | SA = 2(6)(4) + 3(6)(3) = 48 + 54 = 102 cm^2 |
| Method 2 | SA = 2A + Ph | SA = 2(12) + 12(3) = 24 + 36 = 60 cm^2 ( incorrect, this method requires more information) |
| Method 3 | SA = lw + 2l√(h^2 + (w/2)^2) + 2w√(h^2 + (l/2)^2) | SA = 24 + 2(6)√(9 + 4) + 2(4)√(9 + 9) = 24 + 12√13 + 8√18 = 102 cm^2 |
| Method 4 | SA = 2lw + l√(h^2 + w^2) + w√(h^2 + l^2) | SA = 48 + 6√(9 + 16) + 4√(9 + 36) = 48 + 6√25 + 4√45 = 102 cm^2 |
| Method 5 | SA = 2A + 3lw | SA = 2(12) + 3(6)(4) = 24 + 72 = 96 cm^2 ( incorrect, this method requires more information) |
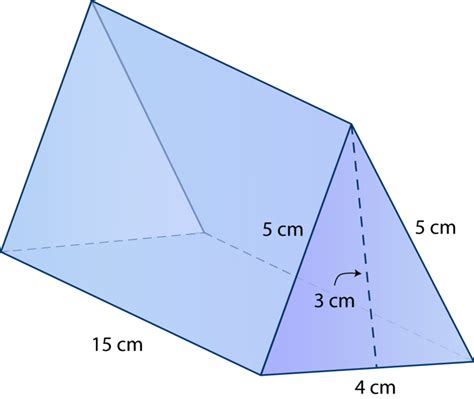
As you can see, the surface area of the triangular prism can be calculated using different formulas, and the result is the same.
Summarizing key points, calculating the surface area of a triangular prism can be done using different formulas, depending on the information available. The five methods presented in this article provide a comprehensive understanding of how to calculate the surface area of a triangular prism. By understanding these formulas, you can apply them to various problems and real-world applications.
What is a triangular prism?
+
A triangular prism is a three-dimensional shape with two identical triangular faces and three rectangular faces.
How do I calculate the surface area of a triangular prism?

+
There are five methods to calculate the surface area of a triangular prism, depending on the information available. You can use the formulas SA = 2lw + 3lh, SA = 2A + Ph, SA = lw + 2l√(h^2 + (w/2)^2) + 2w√(h^2 + (l/2)^2), SA = 2lw + l√(h^2 + w^2) + w√(h^2 + l^2), or SA = 2A + 3lw.
What information do I need to calculate the surface area of a triangular prism?
+
You need to know the length, width, and height of the prism to calculate the surface area using most of the formulas. However, some formulas require additional information, such as the area of the triangular base or the perimeter of the triangular base.