Master Negative Number Subtraction with Free Worksheets

Subtracting negative numbers can seem daunting at first, but with the right approach, it becomes a manageable and even exciting part of arithmetic. This blog post aims to simplify the concept, provide practical exercises, and ensure you or your students can master the art of subtracting negative numbers with ease.
Understanding Negative Numbers

Before diving into subtraction, let's understand what negative numbers are. Imagine numbers on a number line:
- Numbers to the right of zero are positive.
- Numbers to the left of zero are negative.
Here's how we can visualize it:

The Rules of Subtraction

Subtracting negative numbers involves a few simple rules:
- Subtract a positive from a positive: Just subtract normally.
- Subtract a negative from a positive: Add the numbers together (Since you are subtracting a negative number, it's like adding).
- Subtract a positive from a negative: Find the difference between the numbers, keeping the sign of the larger number.
- Subtract a negative from a negative: This is where things get interesting. Here, you are actually adding the numbers together because two minuses make a plus.
Subtracting Positive from Positive

For instance, if you're subtracting 7 from 12:
12 - 7 = 5
Subtracting Negative from Positive

Subtracting -8 from 10:
10 - (-8) = 10 + 8 = 18
Subtracting Positive from Negative

Let's subtract 5 from -3:
-3 - 5 = -8
Subtracting Negative from Negative

Now, subtracting -4 from -2:
-2 - (-4) = -2 + 4 = 2
Practical Application: Worksheets

To reinforce these concepts, let's work through some examples. Here is a table where you can practice the subtraction rules:
| Problem | Solution |
|---|---|
| 15 - (-3) | 15 + 3 = 18 |
| -9 - 4 | -9 + (-4) = -13 |
| -7 - (-7) | -7 + 7 = 0 |
| 8 - (-11) | 8 + 11 = 19 |

⚠️ Note: When subtracting two numbers with the same sign, think of moving along the number line in the same direction.
Tips for Success

- Visualize the Number Line: Always picture numbers on a line to understand their relationships.
- Use Real-life Scenarios: Think of debts (negative numbers) or savings (positive numbers) to make the subtraction relatable.
- Practice Consistently: The more you practice, the more intuitive it becomes.
Let's explore these tips further:
Visualizing with a Number Line

Draw a number line and physically move along it as you calculate. For example:

If you need to subtract -3 from 5, you start at 5 and move 3 steps to the right, ending at 8.
Real-life Scenarios

Imagine you owe someone money (negative), and you borrow more (subtracting another negative), you actually reduce your debt. Here's an example:
- You owe $50 (-50)
- You borrow $30 more (-30)
- So, -50 - (-30) = -50 + 30 = -20, reducing your debt to $20.
Consistent Practice
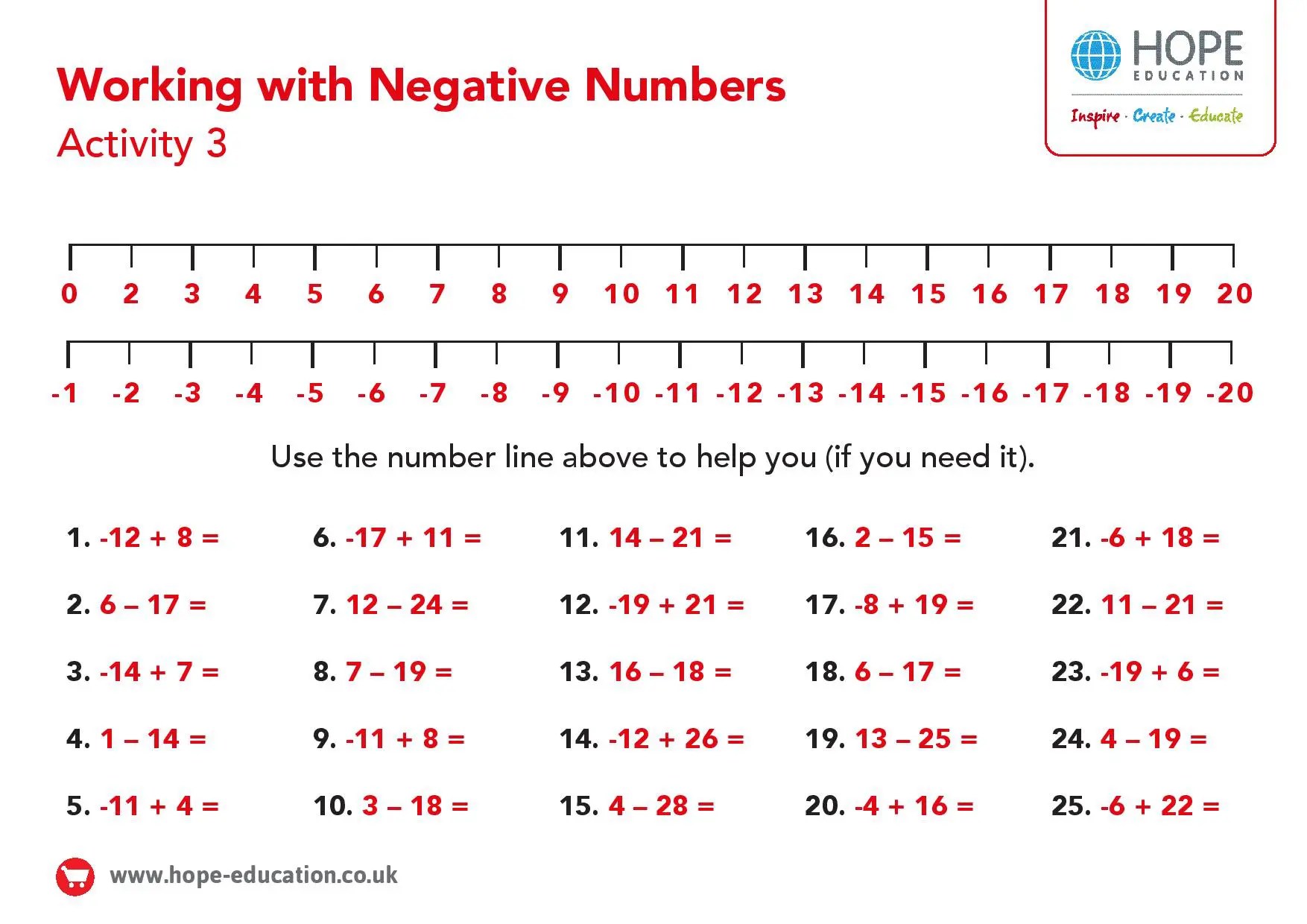
Here are some exercises to help cement your understanding:
- -8 - (-5) = ?
- 12 - (-9) = ?
- -15 - 3 = ?
Your responses should be:
- -8 + 5 = -3
- 12 + 9 = 21
- -15 + (-3) = -18
In wrapping up, mastering the subtraction of negative numbers is an important step in understanding arithmetic and algebra. By following these guidelines, practicing consistently, and relating numbers to real-life scenarios, you can not only become proficient in negative number subtraction but also build a stronger foundation in mathematics as a whole.
What happens when you subtract a negative number from a positive number?

+
When you subtract a negative number from a positive number, it’s equivalent to adding the two numbers together. For instance, 10 - (-8) equals 10 + 8 = 18.
Is it possible to have two minuses in a row?

+
Yes, when you see a minus followed by another minus in subtraction, it’s effectively like adding the numbers. For example, -5 - (-7) becomes -5 + 7 = 2.
Why do we need negative numbers?

+
Negative numbers are essential in various fields like finance (to represent debts), temperature (to indicate below zero), and in scientific calculations where they represent quantities less than zero.
How can I practice subtracting negative numbers?
+Practice through worksheets, number line visualization, and creating real-life scenarios. Repetitive exercises will enhance your understanding and proficiency.