Standard Form Linear Equation Worksheet Guide

Understanding and solving standard form linear equations is a fundamental skill in algebra. These equations, typically expressed as ax + by = c, where a and b are coefficients, x and y are variables, and c is a constant, provide a framework for graphing lines, solving systems of equations, and understanding relationships between variables. This guide will walk you through how to effectively use and create a worksheet for practicing standard form linear equations.
Creating Your Worksheet
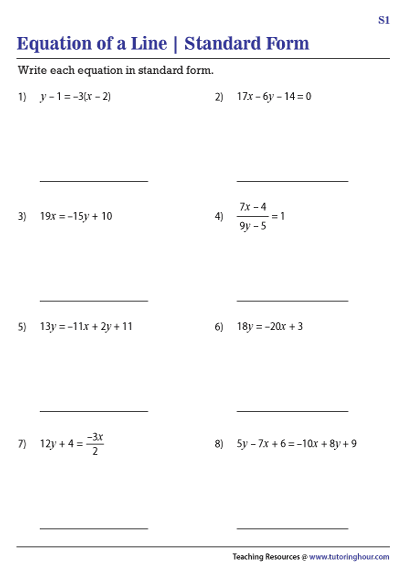
When creating a worksheet focused on standard form linear equations, consider the following steps:
- Define the Objective: Start by setting clear educational goals. Are you teaching students how to convert equations, graph them, or solve them algebraically?
- Select Equations: Include a variety of standard form linear equations with different coefficients, intercepts, and slopes. Here's a sample:
| Equation | Objective |
|---|---|
| 2x + 3y = 6 | Conversion to slope-intercept form |
| 4x - y = -2 | Solving for one variable |
| -x + y = 5 | Finding intercepts |

- Instructions: Provide clear and concise instructions for each section of your worksheet. Use bullet points:
- Convert each equation to slope-intercept form (y = mx + b).
- Solve for one of the variables.
- Graph the line using the intercepts or slope-intercept form.
💡 Note: Ensure that the complexity of the equations matches the level of your students to avoid unnecessary frustration or boredom.
Using the Worksheet for Learning

Here's how you can utilize the worksheet effectively:
- Group Work: Use the worksheet for peer learning, where students can work together to solve problems.
- Guided Practice: Walk through examples with the students, showing how to solve or graph each type of equation.
- Independent Study: Allow time for students to work on their own, checking their answers later with provided solutions.
Tips for Engagement

- Make it Visual: Include diagrams or graph paper where students can sketch their solutions.
- Real-World Applications: Link equations to real-life scenarios to illustrate their relevance.
- Challenges: Offer optional problems that are more complex for advanced learners.
Incorporating Technology

Technology can enhance learning:
- Graphing Calculators: Use them to verify student solutions and deepen understanding.
- Interactive Tools: Websites like Desmos can be used for dynamic graphing of lines.
- Online Quizzes: Create quizzes with immediate feedback to reinforce learning.
🌐 Note: Leverage technology to foster a more interactive and engaging learning experience, but ensure it complements rather than replaces manual calculations.
Assessments

Assessments are crucial for measuring understanding:
- Homework: Assign worksheet problems as homework to practice concepts independently.
- Quizzes: Use short quizzes to check for understanding of key concepts like graphing and solving.
- Exams: Include more complex questions that require students to apply what they've learned comprehensively.
To wrap up, a worksheet on standard form linear equations isn't just about solving equations; it's an opportunity to build a deeper understanding of algebraic concepts. By carefully crafting your worksheet, you can engage students, introduce them to real-world applications, and prepare them for more advanced math topics. Through a combination of structured practice, technology, and assessments, educators can ensure that students not only understand how to manipulate these equations but also see their utility in practical contexts.
What is the standard form of a linear equation?

+
The standard form of a linear equation is ax + by = c, where a, b, and c are constants, and x and y are variables.
Why use standard form over slope-intercept form?

+
Standard form is often preferred in solving systems of equations because it provides a simpler way to match coefficients and use methods like substitution or elimination. It also emphasizes the balance between variables.
Can real-world problems always be modeled by standard form equations?

+
Yes, many real-world problems that can be represented by a linear relationship can be modeled using standard form. However, some require more complex equations or systems.



