5 Algebra Simplification Tricks You Must Know

Algebra is a cornerstone of mathematics, integral to understanding equations, functions, and even more advanced math concepts. Whether you're a student trying to tackle homework or an adult brushing up on forgotten skills, knowing some shortcuts in algebra simplification can significantly reduce the time spent on calculations and increase your accuracy. Here are five algebra simplification tricks that you must know to streamline your problem-solving process.
1. Distributive Property Mastery

The distributive property is one of the fundamental tools in algebra, which states that a(b + c) = ab + ac. Here’s how to maximize its utility:
- Combine Like Terms: After distribution, look for terms that can be combined to simplify the expression further.
- Reverse Distribution: Sometimes you’ll want to factor an expression by distributing backwards, which can make complex expressions more manageable.
💡 Note: Always distribute the multiplication over addition or subtraction before combining terms.
2. Recognizing Perfect Squares

When working with binomials, recognizing perfect squares can save you considerable time:
- (a + b)2 = a2 + 2ab + b2: Notice that the middle term is double the product of the two terms being squared.
- (a - b)2 = a2 - 2ab + b2: Here, the middle term is subtracted rather than added.
💡 Note: Remember to add or subtract the middle term according to the sign.
3. Using the Difference of Squares

Another binomial form that simplifies calculation is:
a2 - b2 = (a + b)(a - b)
This trick is handy when you want to factor expressions quickly without going through a lengthy polynomial division.
💡 Note: This only applies to perfect squares being subtracted, not added.
4. Simplify Using Substitution
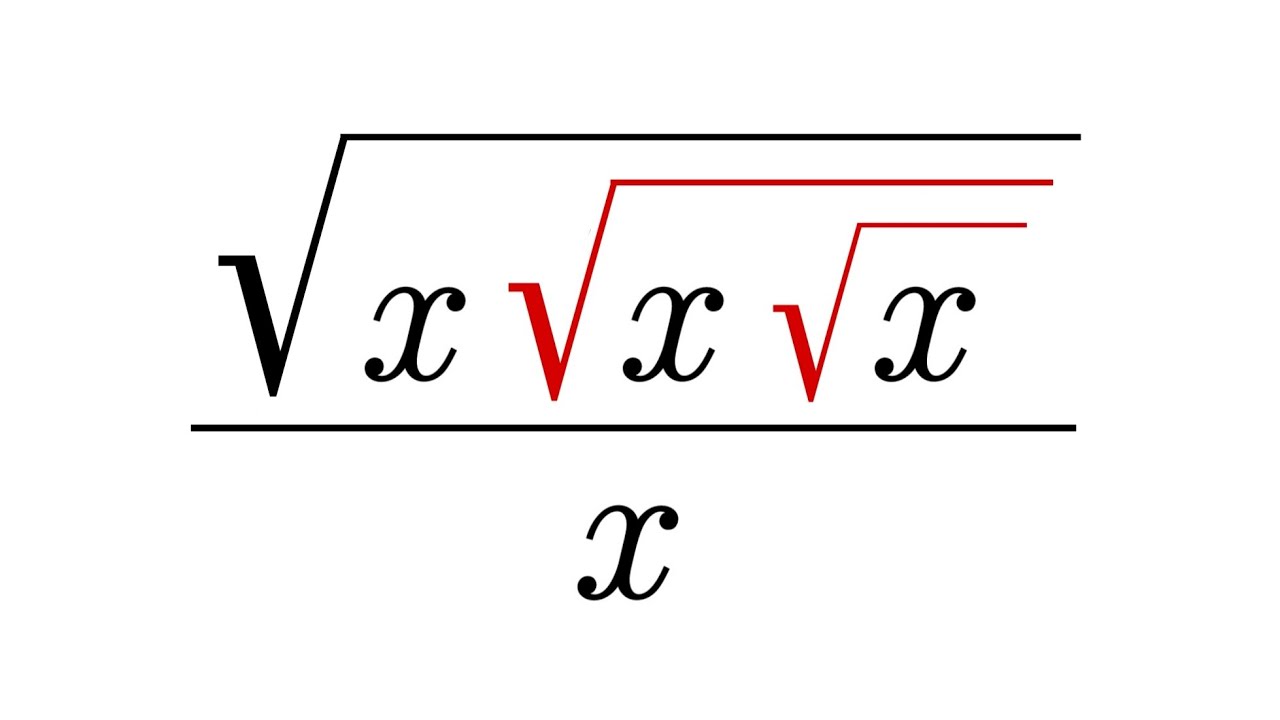
Sometimes, the expression you’re working with can be simplified by substituting one part for another:
- Replace Complex Variables: If an expression contains a variable repeatedly, consider substituting it with something simpler like ‘u’ or ‘x’ to make calculations less cluttered.
- Use Arithmetic Identities: Substituting known arithmetic identities or recognizing patterns can simplify expressions significantly.
💡 Note: Be sure to reverse the substitution to get your final answer in terms of the original variables.
5. Employing Symmetry and Structure
Algebra is often about finding patterns and structures. Look for symmetry in your equations:
- Symmetry in Polynomials: If a polynomial has symmetrical terms, it might be symmetrical in its solutions or factorization as well.
- Structure of Linear Systems: Understand how equations can be combined to simplify systems of linear equations.
💡 Note: Symmetry often suggests that terms or equations can be grouped or added in ways that simplify the problem.
These algebra simplification tricks are not just time-savers; they help foster a deeper understanding of algebraic concepts. By mastering these techniques, you'll not only solve problems faster but also see the beauty and logic in algebra. Whether it's recognizing the forms of expressions or employing substitution for clarity, each method has its place in your mathematical toolkit. They'll serve you well in a variety of mathematical contexts, from solving basic equations to tackling complex calculus problems.
What is the most common mistake when using the distributive property?
+
The most common mistake is forgetting to distribute the multiplication over both terms inside the parentheses. Always remember to multiply the term outside the parentheses with each term inside.
How can I quickly identify if an expression is a perfect square?

+
Look for the square of the first term (a2), the square of the last term (b2), and a middle term that is twice the product of a and b (2ab).
When should I use the difference of squares?

+
Use this when you see two perfect squares being subtracted from each other. It’s a direct and efficient way to factor expressions without going through standard factorization methods.