5 Simple Tricks for Mastering Square Roots Easily

The concept of square roots might seem intimidating at first, but with the right techniques, anyone can master this fundamental aspect of mathematics with ease. Square roots are essential in various fields, from engineering to finance, and mastering them not only simplifies complex problems but also enhances your overall mathematical prowess. Here are five simple tricks to make calculating square roots a breeze.
1. Estimating with Perfect Squares

The cornerstone of understanding square roots is to know the perfect squares. Here’s how you can leverage this knowledge:
- Learn the squares of numbers from 1 to 20. For example, 12=1, 22=4, 32=9, etc.
- When finding the square root of a number, start by identifying the perfect squares closest to that number. This gives you a range to work within.
- Estimate the root by finding the midpoint between these squares. If the number is closer to a lower square, adjust down; if closer to a higher square, adjust up.
📚 Note: Practice recognizing perfect squares quickly. A chart or flashcards can be invaluable here.
2. The Digit-by-Digit Method

Once you have an estimate, you can refine it using the following steps:
- Divide the number whose square root you seek into pairs from the decimal point.
- Find the largest number whose square is less than or equal to the first pair on the left, write it down, and subtract its square from this pair.
- Bring down the next pair, double the current approximation, and find the digit such that when added to this, the product with itself is less than or equal to the new number.
- Repeat this process until you achieve the desired level of precision.

👁️ Note: This method can be used manually or programmed into a spreadsheet for quick computations.
3. Simplifying Radicals

Often, square roots can be simplified to make calculations easier:
- If the number under the square root has factors that are perfect squares, you can take their square root out of the radical.
- For example, √50 = √(25*2) = 5√2.
✨ Note: This trick is particularly useful in algebra and geometry where expressions need to be simplified for clarity.
4. Using the Babylonian Method

This ancient technique provides an iterative approach to find increasingly accurate approximations of square roots:
- Start with an initial guess, g.
- Compute the next guess using: gnext = (g + n/g) / 2, where n is the number whose square root you’re finding.
- Repeat until the difference between two consecutive guesses is sufficiently small.
♻️ Note: This method converges quickly, making it efficient for computational environments.
5. Making Use of Technology

In today’s digital age, technology can handle the heavy lifting of square root calculations:
- Use a scientific calculator or the calculator app on your smartphone.
- Employ online calculators designed specifically for square roots, such as WolframAlpha or Desmos.
- Use computer software like MATLAB or R for more complex root-finding tasks.
By employing these five simple tricks, you'll find that what once seemed like an intimidating task becomes manageable and even enjoyable. The ability to calculate square roots not only boosts your confidence in math but also opens doors to understanding more advanced mathematical concepts. Whether you're solving equations, analyzing data, or just pursuing personal interest, these techniques will serve you well.
Why is it important to know square roots?

+
Understanding square roots is essential for various mathematical operations, including solving quadratic equations, simplifying expressions, and working with distances or areas in geometry and physics.
Can I use these methods for other types of roots?
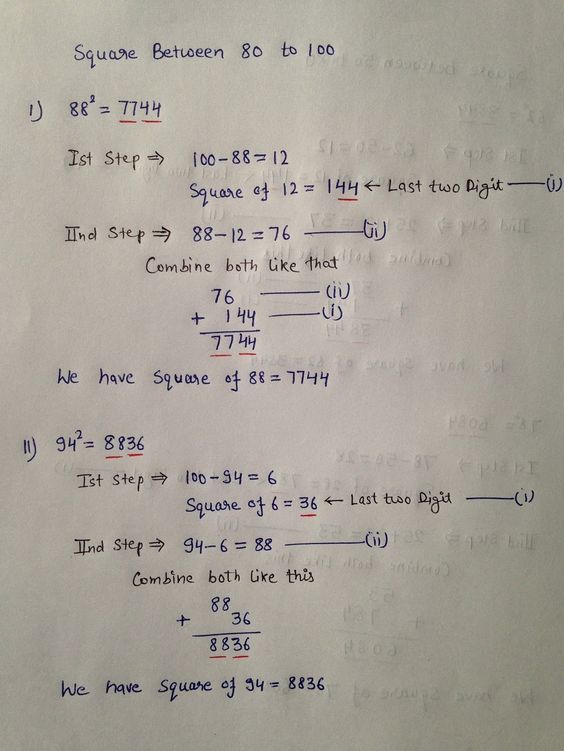
+
Yes, while the focus here was on square roots, the digit-by-digit method and the Babylonian method can be adapted for cube roots and other higher roots, although they might require slight adjustments.
How accurate are these methods for large numbers?

+
The accuracy improves with each iteration of the Babylonian method, while the digit-by-digit method can be as accurate as you’re willing to spend time on. However, for very large numbers, using a calculator or software might be more practical.



