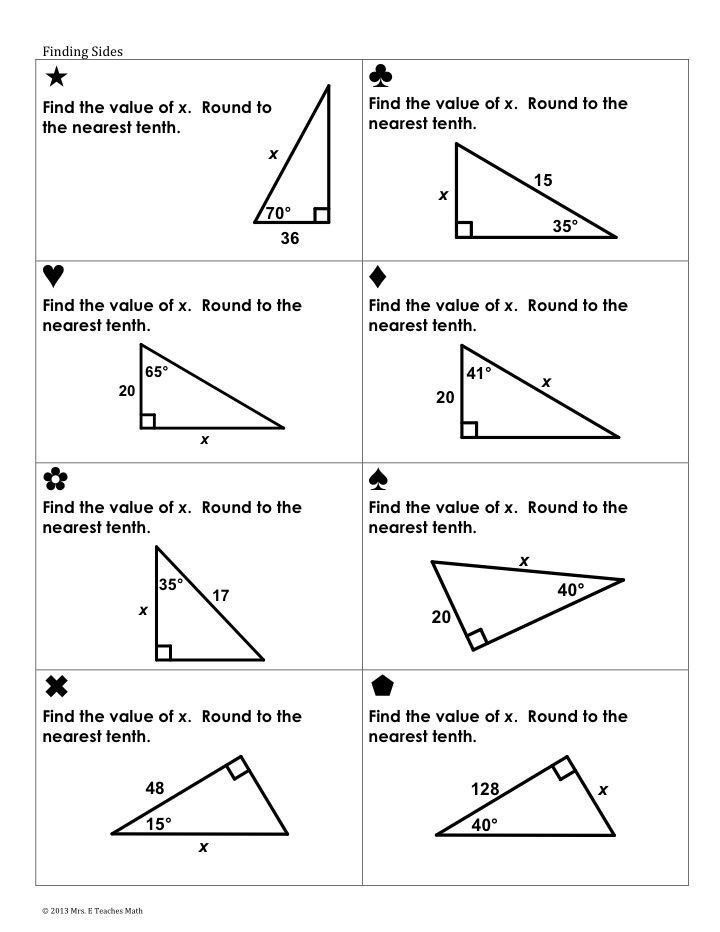
Master Special Segments in Circles Easily with This Worksheet

Understanding special segments in circles is vital for students and enthusiasts of geometry alike. These segments, often seen in circles, include diameters, chords, secants, and tangents, each with unique properties and behaviors. This blog post will guide you through these segments with clarity, using a worksheet designed for easy learning. Here's how you can master these critical circle segments effectively.
Chord: Basics and Properties

A chord is a line segment with both endpoints on the circumference of a circle. Here are some key features:
- The diameter is the longest possible chord and passes through the circle’s center.
- A perpendicular from the center of the circle to a chord bisects the chord.
- Chords equidistant from the center are equal in length.
Worksheet Example:
| Chord Length (cm) | Distance from Center (cm) | Chord Length Calculated |
|---|---|---|
| 10 | 3 | √64 = 8 cm |
| 12 | 4 | √64 = 8 cm |
| 15 | 5 | √100 = 10 cm |

Your task:
- Measure the chords and determine if the perpendicular bisectors are equidistant.
- Confirm or calculate the length of the chords based on their distance from the center.
📝 Note: Ensure to use a precise ruler to measure chord lengths and distances from the center.
Secant and Tangent: Interactive Learning
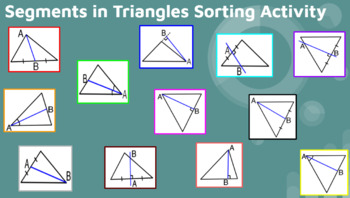
Here, we’ll delve into secants, which are lines that intersect a circle at two points, and tangents, which touch the circle at exactly one point.
- A secant can be thought of as a chord extended beyond the circle, while a tangent is a line perpendicular to the radius at the point of tangency.
- The power of a point theorem states that if two secant lines are drawn from the same external point to a circle, then their power of a point is equal.
Worksheet Example:
1. Secant Problem: Line AB intersects the circle at A and B, and point C lies outside the circle. Measure the length of AC and BC. Calculate the Power of Point C.
2. Tangent Problem: Construct a tangent line from point D to the circle. Calculate the distance from the center of the circle to point D.
Your task:
- Verify the power of a point theorem through calculations.
- Explore the geometric relationship between tangents and secants using given measurements.
📚 Note: Sketch the secant and tangent lines carefully to understand their spatial relationship with the circle.
Diameters and Their Special Properties

A diameter, being the longest chord, has some unique properties:
- It passes through the center of the circle, dividing it into two equal semicircles.
- Every diameter is a chord, but not every chord is a diameter.
- The diameter can be used to calculate the circumference and area of the circle using π.
Worksheet Example:
1. Diameter Length: If the circumference of the circle is 25.13 inches, calculate the length of the diameter.
2. Area Calculation: Given a diameter of 10 cm, find the area of the circle.
Your task:
- Use the diameter measurements provided to solve these problems and verify your solutions.
Understanding special segments in circles is not just about solving problems; it’s about appreciating the symmetry and beauty of these geometric relationships. By engaging with the provided worksheet, you not only reinforce your knowledge but also gain a deeper understanding of the circle’s geometry.
What is the difference between a chord and a diameter?

+
A chord is any straight line segment with both endpoints on the circle, while a diameter is the longest possible chord, which passes through the center and divides the circle into two equal semicircles.
Can a secant and a tangent intersect each other in a circle?

+
A secant and a tangent can indeed intersect outside of the circle. At the point of tangency, the tangent is perpendicular to the radius of the circle.
How do you calculate the length of a chord if the distance from the center is known?

+
You can use the formula: Chord Length = 2 * √(r² - d²), where r is the radius and d is the perpendicular distance from the center to the chord.