5 Ways to Solve Special Right Triangles in a Maze

Understanding the Basics

The world of mathematics presents numerous puzzles that test our problem-solving skills, and solving Special Right Triangles in a maze is one such intriguing challenge. Understanding the principles behind these triangles and how to navigate mazes can be both fun and educational. Let’s dive into how you can conquer this unique problem with five practical methods.
Method 1: The 30-60-90 Triangle Rule

The 30-60-90 triangle, also known as an isosceles right triangle, is one of the most frequently appearing special right triangles in a maze. Here’s how you can use its properties to find your way:
- Identify the Triangle: Look for any triangle where one angle measures 30 degrees and another 60 degrees.
- Apply the Ratio: In a 30-60-90 triangle, the sides are always in the ratio 1 : √3 : 2. This means:
- The short side opposite the 30-degree angle is the shortest (let’s call it x).
- The side opposite the 60-degree angle is x√3.
- The hypotenuse, opposite the right angle, is 2x.
- Navigate the Maze: Use these ratios to calculate missing sides and determine your next move.
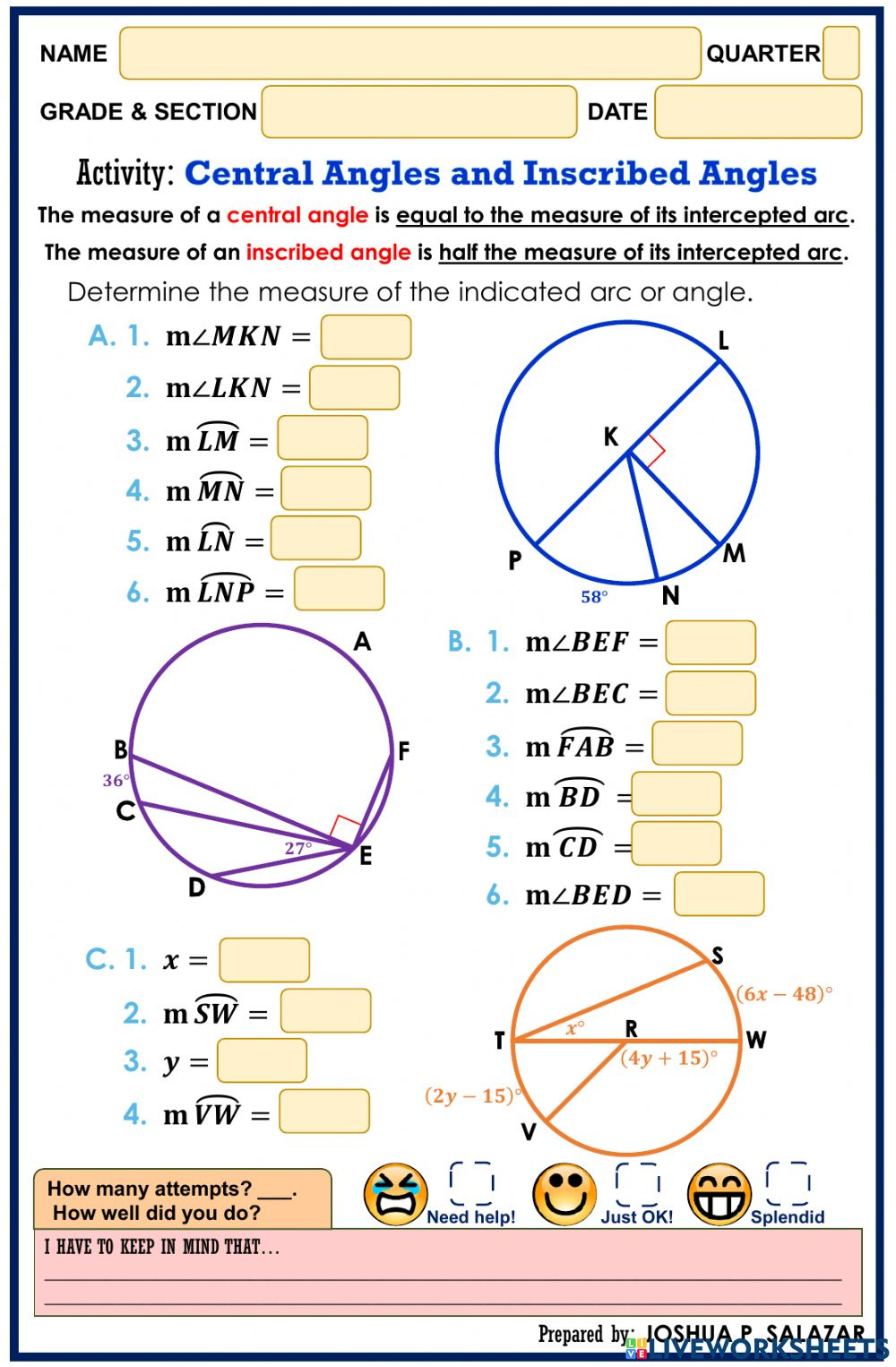
Method 2: The 45-45-90 Triangle Rule

Another type of special right triangle is the 45-45-90 triangle, which you’ll also find in mazes. Here’s the step-by-step process:
- Spot the Triangle: Look for triangles with two 45-degree angles and one right angle.
- Understand the Ratio: The sides of a 45-45-90 triangle are in the ratio 1 : 1 : √2. Specifically:
- Both legs are equal in length (let’s call them x).
- The hypotenuse is x√2.
- Find Your Way: Use this ratio to find missing sides, helping you navigate through the maze more effectively.
📝 Note: Remember that the hypotenuse of a 45-45-90 triangle will always be √2 times one of its legs.
Method 3: Applying Trigonometric Identities
Trigonometry is a powerful tool when the maze presents triangles without adhering strictly to the special right triangle rules. Here’s how you can use trigonometric functions:
- Sine, Cosine, Tangent: Use SOH-CAH-TOA to find angles or sides in any triangle:
- Sine (sin) = Opposite/Hypotenuse
- Cosine (cos) = Adjacent/Hypotenuse
- Tangent (tan) = Opposite/Adjacent
- Calculate Angles: Knowing one side or an angle, you can determine other sides or angles through trigonometric identities.
- Maze Solving: Apply these calculations to find the next path or direction to move in the maze.
Method 4: Using Pythagorean Theorem

Sometimes, you’ll come across triangles in the maze that do not fit into the special categories. Here’s where the Pythagorean theorem becomes useful:
- State the Theorem: a² + b² = c², where ‘c’ is the hypotenuse.
- Find Missing Side: If you know two sides of a right triangle, you can find the third.
- Navigate: Use this to navigate through the maze by calculating distances to move or to understand the layout of your path.
📝 Note: When solving for sides in any right triangle, the Pythagorean theorem is always applicable.
Method 5: Backtracking and Visualization

Solving a maze with triangles also requires strategic thinking beyond just mathematical rules:
- Backtrack: If you reach a dead end, use your knowledge of the triangles’ properties to determine which path you should have taken.
- Visualize: Draw or visualize the maze layout, marking known angles and sides. This can help you see patterns or the overall structure, guiding you towards the exit.
- Map Out: If possible, physically map out the maze as you solve it, noting down key triangle properties at each junction.
In summary, solving special right triangles in a maze combines mathematical knowledge with logical and strategic thinking. By mastering the rules of 30-60-90 and 45-45-90 triangles, understanding trigonometric identities, applying the Pythagorean theorem, and using visualization techniques, you can effectively find your way through these mathematically themed labyrinths. Each method provides different insights and tools, making the journey through the maze not just about reaching the end, but also about understanding the intricate interplay of shapes and angles along the way.
Why are special right triangles used in mazes?

+
Special right triangles are used in mazes because they present a unique challenge that combines logical navigation with mathematical problem-solving, providing an educational and entertaining experience.
Can I solve a maze with triangles without knowing trigonometry?

+
Yes, you can navigate some mazes using only the properties of special right triangles and basic geometry, though advanced knowledge of trigonometry can simplify complex scenarios.
How do I practice for solving such mazes?

+
Practice can include solving practice problems involving right triangles, attempting physical or digital mazes designed with mathematical principles, and understanding how to apply different mathematical concepts in problem-solving scenarios.
What if I encounter an irregular triangle in the maze?

+
Use the Pythagorean theorem to find missing sides if you know two sides or use trigonometric functions to find angles, guiding your navigation through the maze.