Arcs Central Angles And Inscribed Angles Worksheet
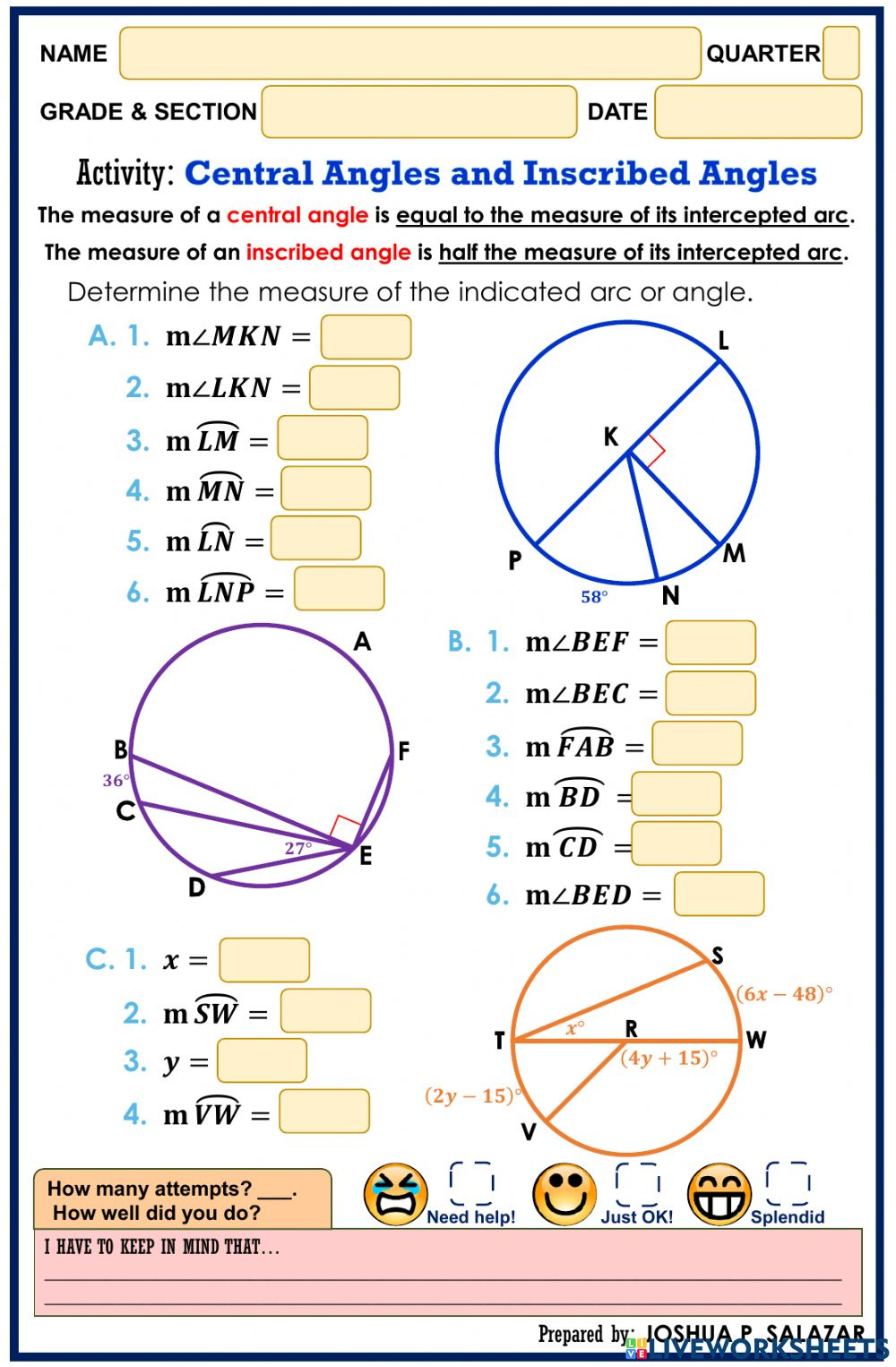
Understanding geometry can be both exciting and challenging, especially when diving into arcs, central angles, and inscribed angles in circles. This topic forms an integral part of high school geometry, enabling students to solve complex problems involving circle properties. This blog post will serve as your comprehensive guide, providing a detailed arcs, central angles, and inscribed angles worksheet, along with explanations to help you grasp these concepts effectively.
Defining Key Terms

Before we delve into the practical exercises, let's clarify the following key terms:
- Arc: A segment of the circumference of a circle.
- Central Angle: An angle whose vertex is the center of the circle and its arms pass through two points on the circle, creating an arc.
- Inscribed Angle: An angle whose vertex lies on the circumference of the circle, and whose sides intersect the circle at two distinct points.
Relationships Between Angles and Arcs

The relationship between the measure of an arc and the angles it subtends is crucial:
- A central angle's measure is equal to the measure of the arc it subtends.
- An inscribed angle's measure is half the measure of the arc it subtends.
The Worksheet

| Problem | Solution Steps | Answer |
|---|---|---|
| 1. If the measure of arc AB is 60 degrees, what is the measure of the central angle? | The central angle equals the arc measure. Thus, 60 degrees. |
60 degrees |
| 2. What is the inscribed angle that subtends an arc of 100 degrees? | Since the inscribed angle is half of the arc, we divide 100 degrees by 2. | 50 degrees |
| 3. If an inscribed angle measures 35 degrees, what is the measure of the arc it subtends? | Arc measure is double the inscribed angle. So, 35 degrees * 2 = 70 degrees. |
70 degrees |
| 4. Given a central angle of 80 degrees, find the measure of the intercepted arc. | Central angle equals intercepted arc. Thus, 80 degrees. |
80 degrees |

💡 Note: Remember that the measure of an arc is always given in degrees, unless otherwise specified.
Solving Complex Problems

Let's look at how we can use these properties in more complex scenarios:
Example 1: If an arc of a circle spans 120 degrees, find the measure of an inscribed angle that subtends:
- One endpoint of the arc.
- Another inscribed angle which subtends the same arc.
Solution:
- An inscribed angle subtending an arc of 120 degrees is 60 degrees.
- Any other inscribed angle subtending the same arc would also be 60 degrees, as all inscribed angles subtending the same arc are congruent.
📌 Note: This rule applies to any inscribed angles subtending the same arc, providing a powerful tool for solving geometric problems involving circles.
Conclusion

By now, you should have a solid understanding of how arcs, central angles, and inscribed angles relate to one another in the context of circles. These relationships not only help in solving geometry problems but also illustrate the beautiful symmetry and properties inherent in circles. Whether you're studying for an exam or simply interested in geometry, using these concepts can enhance your spatial reasoning and problem-solving skills. Remember, practice with this worksheet will reinforce your understanding and ability to apply these principles in varied contexts.
What is the difference between a central angle and an inscribed angle?

+
A central angle has its vertex at the center of the circle, and its measure equals the measure of the arc it subtends. An inscribed angle, however, has its vertex on the circle’s circumference, and its measure is half the measure of the arc it subtends.
How do you find the measure of an arc?

+
To find the measure of an arc, if you know the central angle, you can use that measure directly since it equals the arc’s measure. For an inscribed angle, multiply its measure by 2 to get the arc measure.
Can the measure of an inscribed angle be greater than 90 degrees?

+
No, an inscribed angle cannot be greater than 90 degrees because the arc it subtends would need to be 180 degrees or more, which would require the angle’s vertex to be on a straight line, making it a diameter (180 degrees) rather than an inscribed angle.
How can I use these properties in practical problems?

+
These properties are useful in architecture, design, surveying, and any field involving circular or semicircular forms. They help in calculating distances, angles, and spatial relationships in real-world applications.
What are some common mistakes when working with these angles?

+
Common mistakes include confusing central angles with inscribed angles, not considering that all inscribed angles subtending the same arc are equal, and misinterpreting the sum of angles around a circle or semicircle.