5 Must-Know 45-45-90 Triangle Worksheet Answers
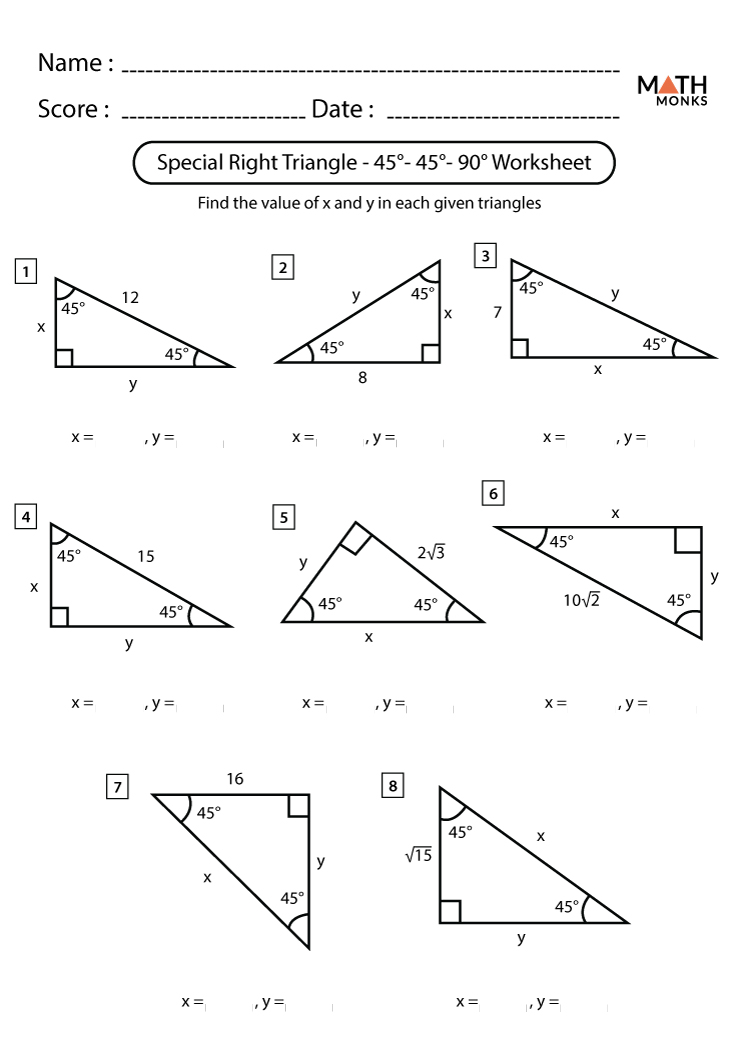
Understanding the 45-45-90 triangle is crucial not only for students of geometry but also for anyone interested in the fascinating world of mathematics. These special right triangles are not just figures on a page; they represent foundational principles that apply in various fields like engineering, architecture, and navigation. This blog post will delve into five key aspects of the 45-45-90 triangle worksheets, providing answers, insights, and practical applications to enhance your understanding.
The Fundamentals of 45-45-90 Triangles
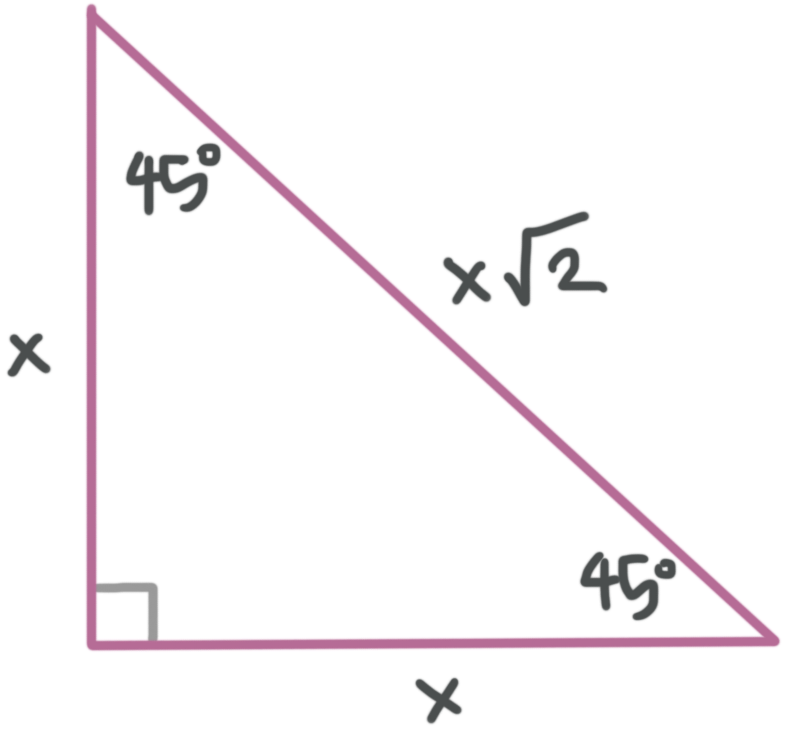
Before we dive into specific worksheet answers, let’s quickly review the basics of the 45-45-90 triangle:
- Angles: This triangle has angles measuring 45°, 45°, and 90°.
- Sides: The hypotenuse (the longest side opposite the right angle) is always √2 times the length of each leg.
- Properties: It’s an isosceles right triangle where the two legs are equal in length.
🏗️ Note: In real-world applications, this triangle often helps in calculating distances in construction or land surveying.
Worksheet Answers: Common Problems
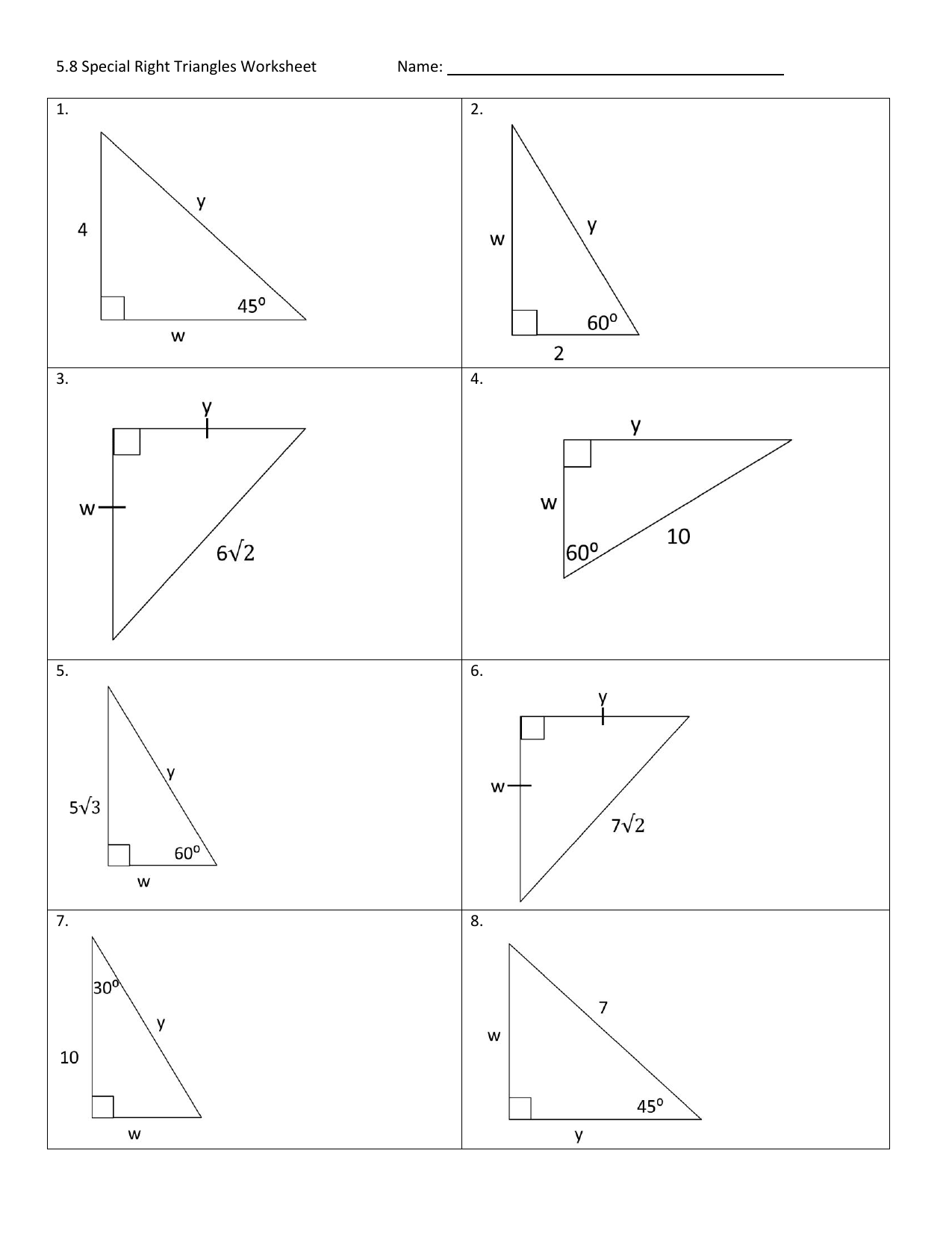
Let’s tackle some typical problems you might find in a 45-45-90 triangle worksheet:
- Finding the Hypotenuse: If each leg of the triangle measures 5 units, the hypotenuse will be:
- hypotenuse = leg * √2 = 5 * √2 = 5√2
<li><strong>Given Hypotenuse, Find Leg Length</strong>: With a hypotenuse of 8√2 units:</li>
<ul>
<li>leg = hypotenuse / √2 = 8√2 / √2 = 8</li>
</ul>
<li><strong>Area Calculation</strong>: For a triangle with legs of 6 units each:</li>
<ul>
<li>Area = (leg^2 / 2) = (6^2 / 2) = 36 / 2 = 18</li>
</ul>
<li><strong>Perimeter Calculation</strong>: If the leg length is known as 4 units:</li>
<ul>
<li>Perimeter = 2 * leg + hypotenuse = 2 * 4 + 4√2 = 8 + 4√2</li>
</ul>
<li><strong>Multiple Triangles</strong>: When dealing with an arrangement of several 45-45-90 triangles:</li>
<ul>
<li>Understand the relationships between the triangles' sides to solve for missing lengths or angles.</li>
</ul>
Practical Applications of 45-45-90 Triangles

Here are some areas where these triangles are particularly useful:
- Architecture: Designing square bases for buildings where stairs need a certain rise or run.
- Engineering: Calculating force vectors or stress analysis in structures.
- Navigation: Determining distances in sailing or flying using the sextant method.
⚠️ Note: The 45-45-90 triangle often comes into play when using Pythagorean theorem in non-rectangular situations.
Tips for Mastering 45-45-90 Triangle Problems

To excel in solving 45-45-90 triangle problems, consider these tips:
- Visualize: Always sketch the triangle to better understand the problem.
- Memorize the ratio: Remember that the hypotenuse is √2 times the leg length.
- Practice: Regularly work on problems to reinforce understanding and speed.
Common Pitfalls and How to Avoid Them

Here are some common errors students make and how to sidestep them:
- Confusing Hypotenuse and Legs: Understand which side is which by identifying the 90° angle.
- Forgetting to Square Root: Remember to multiply by √2 to find the hypotenuse, not add or square.
- Ignoring Right Angle Property: This isn’t any isosceles triangle; it’s a special one with a right angle!
🔍 Note: Misinterpreting the sides of the triangle is a common cause of errors in calculations.
The Importance in Geometry and Trigonometry

The 45-45-90 triangle is foundational in:
- Trigonometric Ratios: Sine, cosine, and tangent for the special angles of 45° are derived from this triangle.
- Coordinate Geometry: Simplifies plotting points and distances in the Cartesian plane.
- Algebraic Problems: Helps in solving for unknown variables in geometric equations.
This recapitulation of 45-45-90 triangles illustrates their omnipresence in mathematical reasoning. With these detailed answers and explanations, students and enthusiasts can sharpen their skills, avoid common mistakes, and apply these triangles in practical scenarios. From engineering to everyday life, this triangle's unique properties offer a lens through which we can understand the underlying symmetry and beauty of geometry.
What are the trigonometric values for a 45° angle in a 45-45-90 triangle?

+
In a 45-45-90 triangle, sin(45°) = cos(45°) = 1 / √2 = √2 / 2, and tan(45°) = 1.
How can I verify if my calculations for a 45-45-90 triangle are correct?

+
Verify by checking if the ratio between the legs and hypotenuse is √2. Also, ensure that the sum of the angles equals 180° and one angle is 90°.
Why do 45-45-90 triangles play such an important role in engineering and architecture?
+
These triangles provide a predictable relationship between their sides, which is crucial for accurate measurements in design, stability, and stress analysis in structures.



