Special Right Triangles Worksheet Answer Key Revealed
Understanding special right triangles is crucial in mathematics, especially when dealing with geometry and trigonometry. In this comprehensive guide, we're going to uncover the intricacies of special right triangles, particularly the 30-60-90 and 45-45-90 triangles, through detailed explanations and a worksheet answer key. This will enhance your comprehension, help in solving problems with ease, and prepare you for real-life applications of these geometric principles.
Understanding Special Right Triangles

Special right triangles are triangles whose angles are fixed, leading to specific side length relationships that simplify calculations and solving geometric problems. Here’s why you should care:
- Consistent Ratios: Understanding these ratios helps in quick mental calculations.
- Solving Complex Geometry: Knowledge of these triangles can simplify problems in physics, architecture, and engineering.
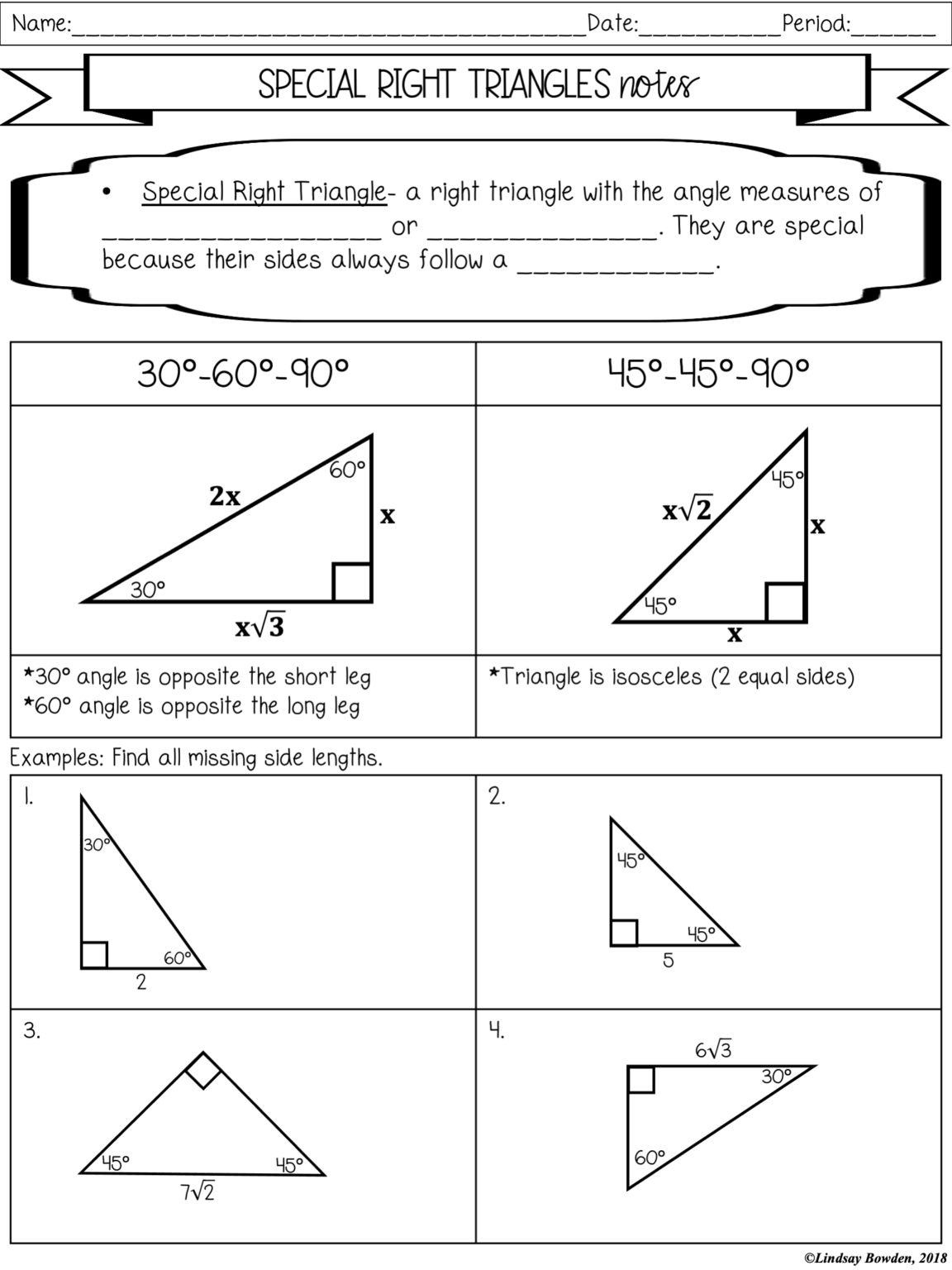
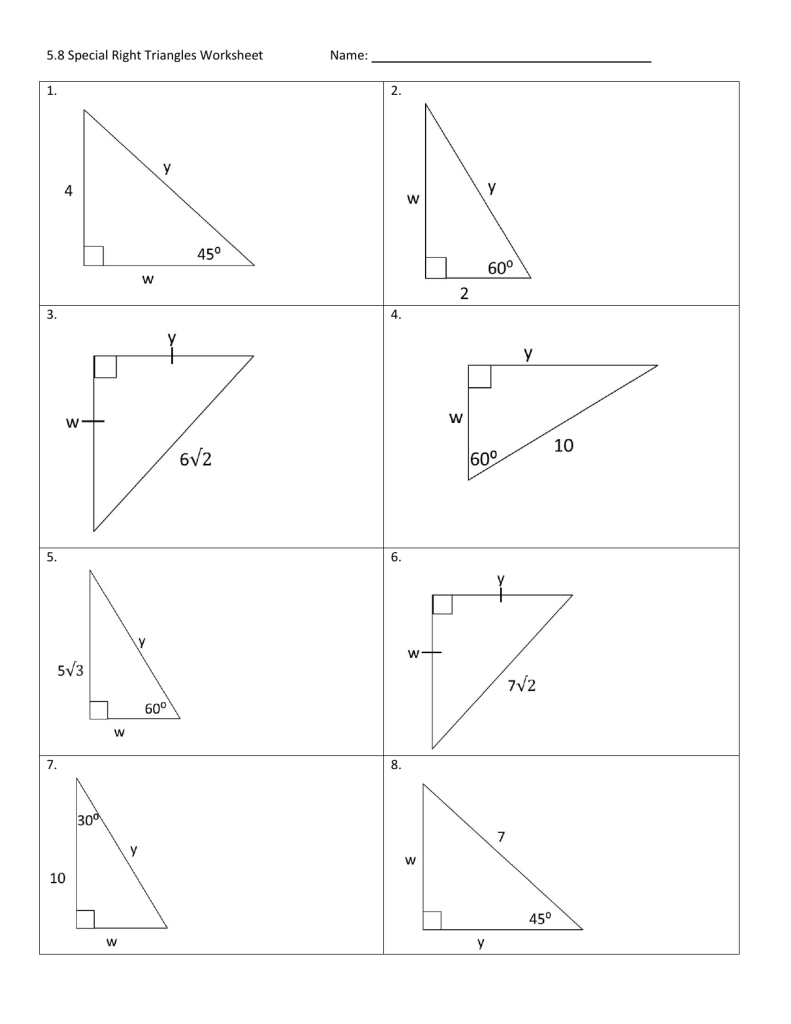
The 30-60-90 Triangle
A 30-60-90 triangle is defined by its angles where one angle measures 30 degrees, one 60 degrees, and one 90 degrees. Here are the properties:
- Side Lengths:
- The shortest side (opposite the 30-degree angle) is denoted as x.
- The hypotenuse, opposite the right angle, equals 2x.
- The side opposite the 60-degree angle is x√3.
📚 Note: These ratios are derived from trigonometry. The sine, cosine, and tangent of these angles create these side relationships.
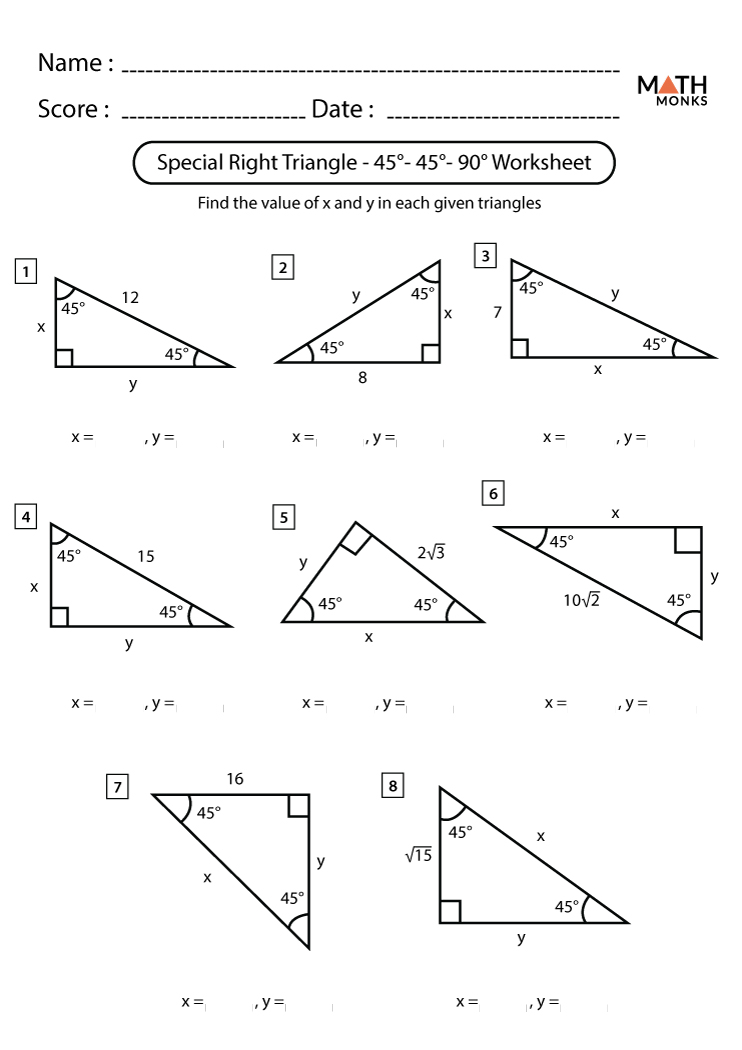
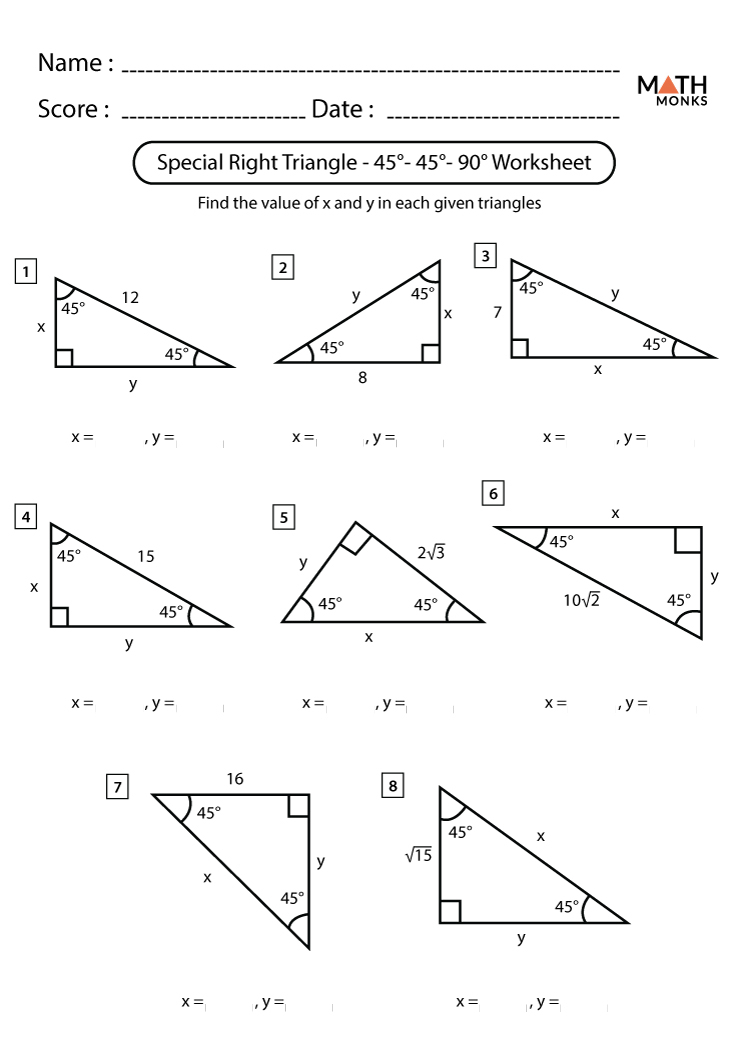
The 45-45-90 Triangle

This triangle features two 45-degree angles with a right angle. Here are the properties:
- Side Lengths:
- Both legs are congruent, each having a length x.
- The hypotenuse equals x√2.
📝 Note: The 45-45-90 triangle is essentially an isosceles right triangle, hence the equal leg lengths.
Applying Special Right Triangles

Let’s delve into practical applications using these triangles:
Worksheet Answer Key

We’ll now provide answers to common problems related to special right triangles:
30-60-90 Triangle Problems:
- If the hypotenuse is 6, find the lengths of the other two sides:
- Shortest side (x) = 6 / 2 = 3
- Side opposite 60 degrees (x√3) = 3√3
- If the side opposite 60 degrees is 4√3, find the hypotenuse and the shortest side:
- Shortest side (x) = (4√3) / √3 = 4
- Hypotenuse (2x) = 2 × 4 = 8
45-45-90 Triangle Problems:
- If one leg of the triangle is 5, find the other leg and the hypotenuse:
- Other leg (x) = 5
- Hypotenuse (x√2) = 5√2
- If the hypotenuse is 8, find the length of each leg:
- Leg (x) = 8 / √2 = 8√2 / 2 = 4√2
These answers illustrate how to solve special right triangles using their unique side ratios.
🌍 Note: Real-world applications often require approximations. For example, 2.828 might be used as an approximation for √2.
In conclusion, special right triangles serve as a fundamental tool in geometry and related fields. The 30-60-90 and 45-45-90 triangles provide shortcuts in solving problems, from calculating unknown side lengths to understanding trigonometric functions and their applications in various scenarios. Mastering these concepts not only enhances mathematical problem-solving skills but also prepares you for advanced studies in fields requiring precise geometrical knowledge.
What are the benefits of learning about special right triangles?

+
Understanding special right triangles provides insights into trigonometry, geometry, and simplifies complex calculations. They’re prevalent in construction, navigation, and various mathematical proofs.
How do I identify a special right triangle?
+
Look for triangles with specific angle combinations like 30-60-90 or 45-45-90. These triangles have unique side relationships.
Are there any common mistakes when solving special right triangles?
+
Common mistakes include misidentifying the triangles, incorrect application of side ratios, and confusion between trigonometric identities.

