Mastering Square Root Equations: Solve with Confidence

Understanding how to solve square root equations can open up a world of mathematical possibilities. Square root equations are fundamental in algebra, and mastering them can enhance your problem-solving skills for more complex mathematical challenges. This blog post is your comprehensive guide to understanding and solving square root equations with ease and confidence.
Basics of Square Root Equations

At the core of algebra, square root equations are a type of equation where the variable appears under the square root sign. Here’s a basic overview of what these equations entail:
- The general form of a square root equation is
√x = b, wherexis the variable we’re solving for. - By squaring both sides of this equation, we can eliminate the square root, allowing us to isolate
x:(√x)² = b², which simplifies tox = b². - This method works perfectly if there are no other terms or if the square root is isolated on one side of the equation.

How to Solve Simple Square Root Equations

Let’s dive into solving these equations step by step:
- Isolate the square root expression: If necessary, rearrange your equation to ensure the square root term stands alone on one side.
- Square both sides to eliminate the square root: Squaring both sides ensures that you get rid of the radical, but remember, this can introduce extraneous solutions.
- Solve the resulting equation: Once the square root is gone, solve the equation for
xusing algebra rules. - Check for extraneous solutions: Since squaring can introduce non-equations into solutions, verify all solutions by substituting them back into the original equation.
Example: Solving a Square Root Equation

Consider the equation √x = 3:
- Isolate the square root, which it already is in this case.
- Square both sides:
(√x)² = 3²→x = 9 - Check the solution: Substitute
x = 9back into the original equation to ensure it’s valid:√9 = 3, which holds true.
Thus, x = 9 is indeed a solution.
Equations with Radicals on Both Sides

When radicals appear on both sides of an equation, the process involves several steps:
- Isolate one of the square roots if possible.
- Square both sides, but do this carefully to avoid issues with extraneous solutions.
- Simplify and check for extraneous solutions again.
Example: Square Roots on Both Sides

Let’s solve the equation √x + 2 = √(2x + 3):
- Isolate a square root:
√x = √(2x + 3) - 2 - Square both sides:
(√x)² = [√(2x + 3) - 2]² - Expand the right-hand side:
x = (2x + 3) - 4√(2x + 3) + 4 - Simplify:
x = 2x + 7 - 4√(2x + 3) - Move terms to isolate the square root:
-x - 7 = -4√(2x + 3) - Square both sides again to eliminate the remaining square root:
(-x - 7)² = (-4)² * (2x + 3) - Expand and simplify: This leads to a quadratic equation, which you can then solve.
- Finally, check for any extraneous solutions by substituting back into the original equation.
Equations with Multiple Radicals
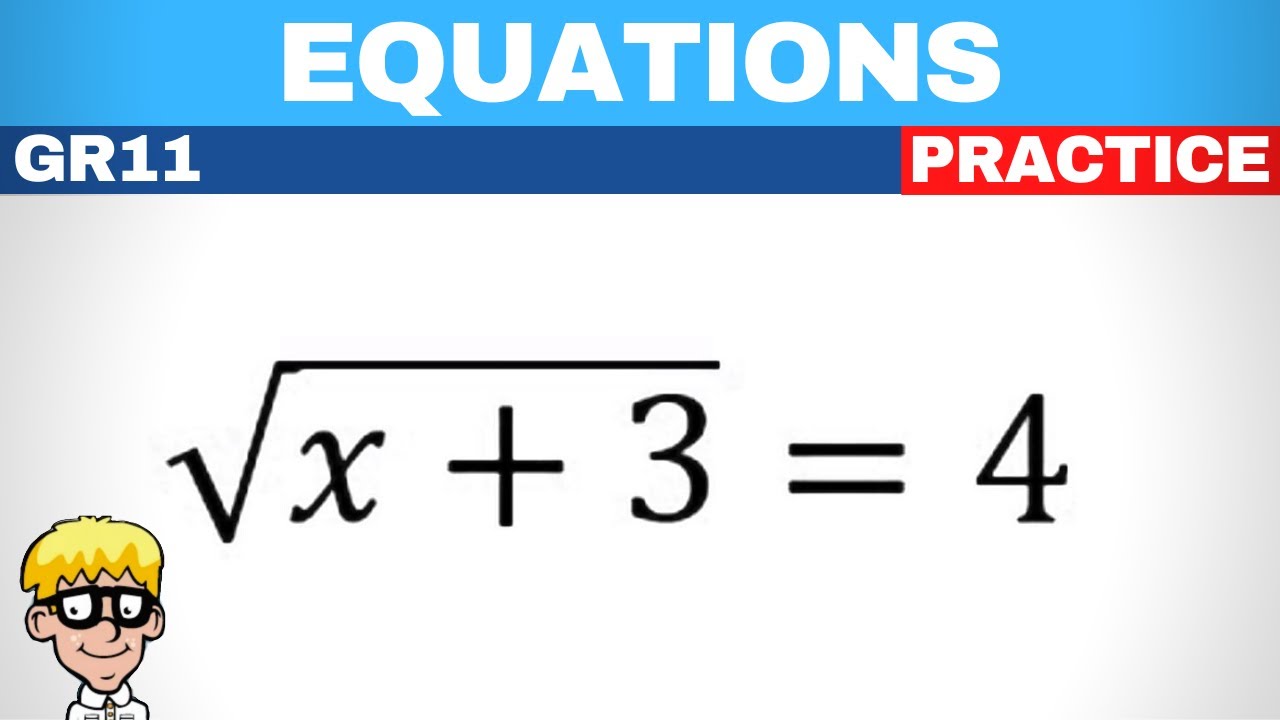
Handling equations where multiple square roots appear requires extra caution:
- Isolate one radical at a time.
- Square both sides to eliminate that radical, then proceed as with simpler equations.
- Watch out for extraneous solutions, as each squaring step can introduce them.
Notes on Square Root Equations

✅ Note: Square roots can only yield positive values, so check for negative solutions after squaring both sides to ensure they’re valid.
📝 Note: Extraneous solutions can occur when squaring both sides of an equation. Always verify the solution by substituting back into the original equation.
Now that we've explored several methods to solve square root equations, let's summarize the key insights from this journey:
Understanding and solving square root equations can significantly boost your algebraic skills. This post covered various methods from simple isolation to handling equations with radicals on both sides. Here's what to remember:
- Always aim to isolate the square root term.
- When squaring both sides, remember to check for extraneous solutions.
- Be careful when multiple radicals are involved as it requires more steps.
By consistently practicing these methods, you'll become adept at navigating through even the most intricate square root equations. Your proficiency in algebra will not only help in solving these equations but also in understanding more complex mathematical concepts in the future.
What is a square root equation?

+
A square root equation is an algebraic equation where the variable appears under the square root sign.
Why do we square both sides of the equation?

+
Squaring both sides of an equation containing a square root helps to remove the radical, allowing you to solve for the variable more directly.
How can I avoid introducing extraneous solutions?

+
After solving, always check your solution by substituting it back into the original equation to ensure it’s valid.
Related Terms:
- Solving square root Equations pdf
- Solving square Equations worksheet pdf



