5 Ways to Master Multi Step Equations Worksheets

Unlocking the Secrets of Multi-Step Equations

Mastering multi-step equations is a crucial skill for students to succeed in mathematics, particularly in algebra and beyond. These types of equations require a combination of skills, including simplifying expressions, solving linear equations, and using inverse operations. In this blog post, we will explore five ways to master multi-step equations worksheets, providing you with practical tips and strategies to help you tackle these challenging equations.
1. Simplify the Equation Before Solving
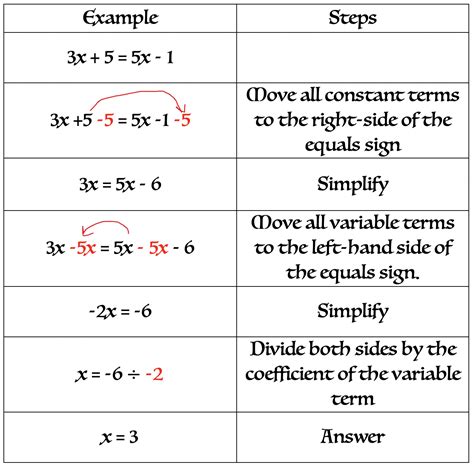
When faced with a multi-step equation, it’s essential to simplify the equation before attempting to solve it. This involves combining like terms, removing parentheses, and simplifying any expressions within the equation. Simplifying the equation can help you identify the operations needed to isolate the variable.
For example, consider the equation: 2(3x + 5) = 12
To simplify this equation, we need to distribute the 2 to the terms inside the parentheses:
2(3x) + 2(5) = 12
This simplifies to:
6x + 10 = 12
Now that the equation is simplified, we can focus on solving for the variable.
📝 Note: Simplifying the equation can also help you identify any common factors or patterns that can aid in solving the equation.
2. Use Inverse Operations to Isolate the Variable

Inverse operations are a crucial concept in solving multi-step equations. Inverse operations involve using the opposite operation to “undo” a particular operation. For example, addition and subtraction are inverse operations, as are multiplication and division.
To isolate the variable, we need to use inverse operations to “get rid” of any constants or coefficients attached to the variable. Using inverse operations can help you isolate the variable and solve the equation.
For example, consider the equation: x/4 + 3 = 7
To isolate the variable, we need to use inverse operations to get rid of the constant term (+3) and the coefficient (1⁄4):
x/4 = 7 - 3
x/4 = 4
To eliminate the coefficient, we can multiply both sides by 4:
x = 4 × 4
x = 16
3. Use the Order of Operations to Evaluate Expressions

When solving multi-step equations, it’s essential to use the order of operations (PEMDAS) to evaluate any expressions within the equation. Following the order of operations ensures that you evaluate the expressions correctly and avoid errors.
For example, consider the equation: 2x + 12 - 3(x - 2) = 20
To evaluate this expression, we need to follow the order of operations:
- Evaluate the expressions inside the parentheses: x - 2
- Multiply the terms: 3(x - 2) = 3x - 6
- Simplify the equation: 2x + 12 - 3x + 6 = 20
- Combine like terms: -x + 18 = 20
Now that the expression is evaluated, we can focus on solving for the variable.
4. Check Your Work and Verify the Solution
Checking your work and verifying the solution is a crucial step in solving multi-step equations. Verifying the solution ensures that your answer is correct and helps you identify any mistakes.
To verify the solution, plug the value of the variable back into the original equation and simplify:
2(3x + 5) = 12
2(3(2) + 5) = 12
2(6 + 5) = 12
2(11) = 12
22 = 12 (Incorrect)
In this example, the solution x = 2 does not satisfy the original equation, indicating an error in the solution.
5. Practice, Practice, Practice!

Mastering multi-step equations requires practice and patience. Regular practice helps you develop problem-solving skills and builds confidence in solving equations.
To improve your skills, try practicing with different types of multi-step equations, such as linear equations, quadratic equations, and polynomial equations. You can also use online resources or worksheets to practice and reinforce your understanding.
What is the difference between a linear equation and a multi-step equation?

+
A linear equation is a type of equation where the highest power of the variable is 1. A multi-step equation, on the other hand, involves more than one operation or step to solve, often requiring the use of inverse operations and simplification.
How do I know if my solution is correct?

+
To verify your solution, plug the value of the variable back into the original equation and simplify. If the equation holds true, then your solution is correct. If not, re-examine your work and try again.
What are some common mistakes to avoid when solving multi-step equations?

+
Some common mistakes to avoid include: failing to simplify the equation, neglecting to use inverse operations, and not verifying the solution.
In conclusion, mastering multi-step equations requires a combination of skills, including simplifying expressions, using inverse operations, and verifying the solution. By following these five tips and practicing regularly, you can develop the skills and confidence needed to tackle these challenging equations. Remember to always check your work and verify the solution to ensure accuracy and avoid errors.
Related Terms:
- solving linear equations worksheets pdf
- solving multi step equations pdf
- solving multi step equations kuta
- multi step equations worksheet printable
- solving equations practice worksheet pdf
- multi equation worksheet 50 questions



