5 Tips to Solve Square Root Equations Easily

Understanding how to solve square root equations is a vital skill for those delving into mathematics, from algebra students to professional mathematicians. This guide will explore five effective strategies to demystify these equations, enabling you to solve them with ease and confidence.
Strategy 1: Understanding the Basics

Before diving into complex equations, it’s important to revisit the fundamentals:
- Definition: A square root of a number (x) is a number (y) such that (y^2 = x).
- Properties: Square roots have properties like non-negativity, symmetry, and simplification rules.
Remember, mastering the basics will help in identifying the nature of the problem before solving it.
Strategy 2: Isolating the Square Root
When dealing with an equation like (\sqrt{x+4} = 6), your goal is to:
- Square both sides: This removes the square root. ((\sqrt{x+4})^2 = 6^2 \Rightarrow x+4 = 36).
- Solve for x: Now, solve the resulting linear equation. (x+4 = 36 \Rightarrow x = 36 - 4 \Rightarrow x = 32).
Strategy 3: Use the Radical Equation Rule
The Radical Equation Rule states that if (a = b) then (a^n = b^n). Here’s how to apply it:
| Equation | Operation | Result |
|---|---|---|
| (\sqrt{x+2} - 5 = 0) | Isolate (\sqrt{x+2}) | (\sqrt{x+2} = 5) |
| (\sqrt{x+2} = 5) | Square both sides | (x + 2 = 25) |
| (x + 2 = 25) | Subtract 2 from both sides | (x = 23) |

Check your solutions by substituting them back into the original equation to ensure there are no extraneous solutions.
Strategy 4: Applying Inverse Operations

This strategy involves:
- Recognizing the need to square both sides to remove square roots.
- Using reciprocals or inverses for roots when dealing with square root inequalities.
Strategy 5: Recognizing Common Pitfalls

There are several common mistakes to avoid:
- Forgetting to check for extraneous solutions. Remember that squaring can introduce solutions that don’t satisfy the original equation.
- Not applying the Radical Equation Rule correctly. The rule must be applied with precision to avoid wrong solutions.
- Ignoring the domain of the function inside the square root. The expression inside the square root must be non-negative.
🔥 Note: Always verify your solutions in the original equation to avoid extraneous results.
In this journey through square root equations, you've learned to isolate variables, apply radical rules, and recognize the importance of checking your solutions. These strategies not only solve equations but also enhance your problem-solving skills, making mathematics not just a subject but an art form. Whether you're a student or a math enthusiast, these techniques will boost your confidence in tackling square root equations.
What is a square root?

+
A square root of a number (x) is a value (y) such that (y^2 = x). It’s the number that, when multiplied by itself, gives the original number.
How can I avoid extraneous solutions when solving square root equations?
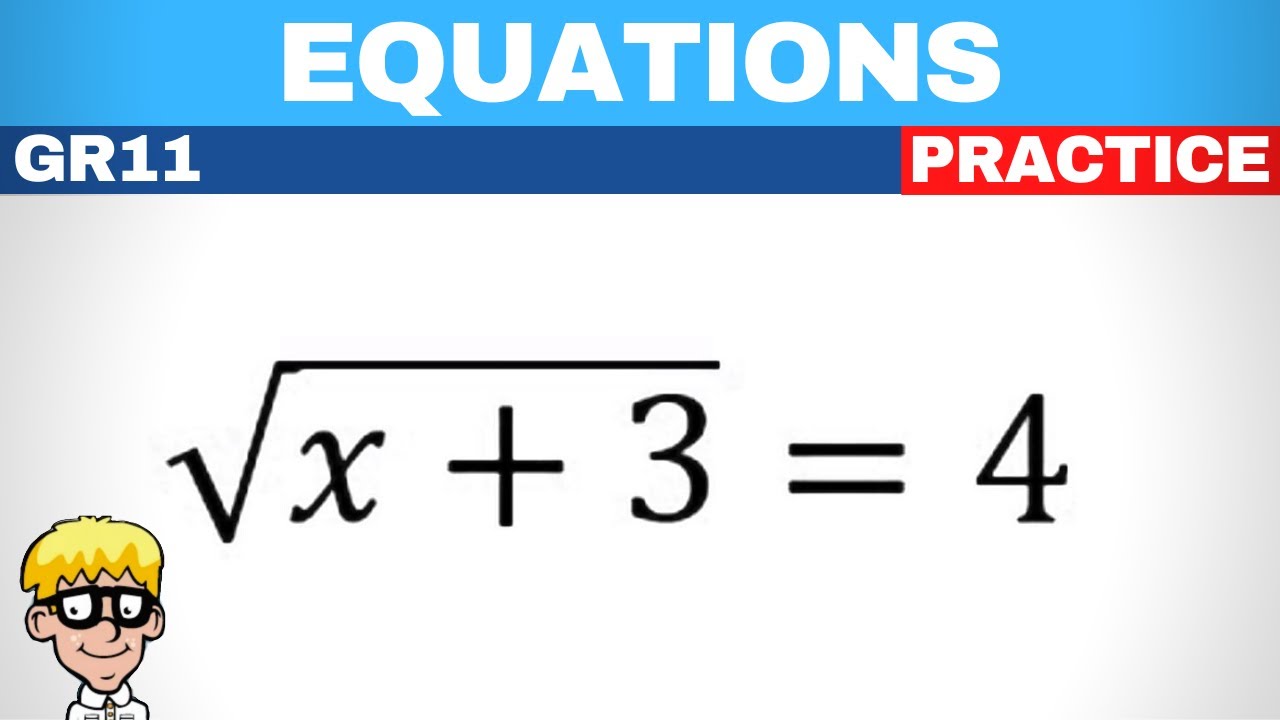
+
Always substitute the solutions back into the original equation. If they make the equation inside the square root negative or do not satisfy the original condition, they are extraneous solutions and should be discarded.
Can you solve a square root equation with a negative root?

+
Generally, in real numbers, taking the square root of a negative number results in a complex or imaginary number. However, in the context of real number solutions, you should solve for the positive root and check for extraneous solutions.