Master Slope Intercept with This Worksheet
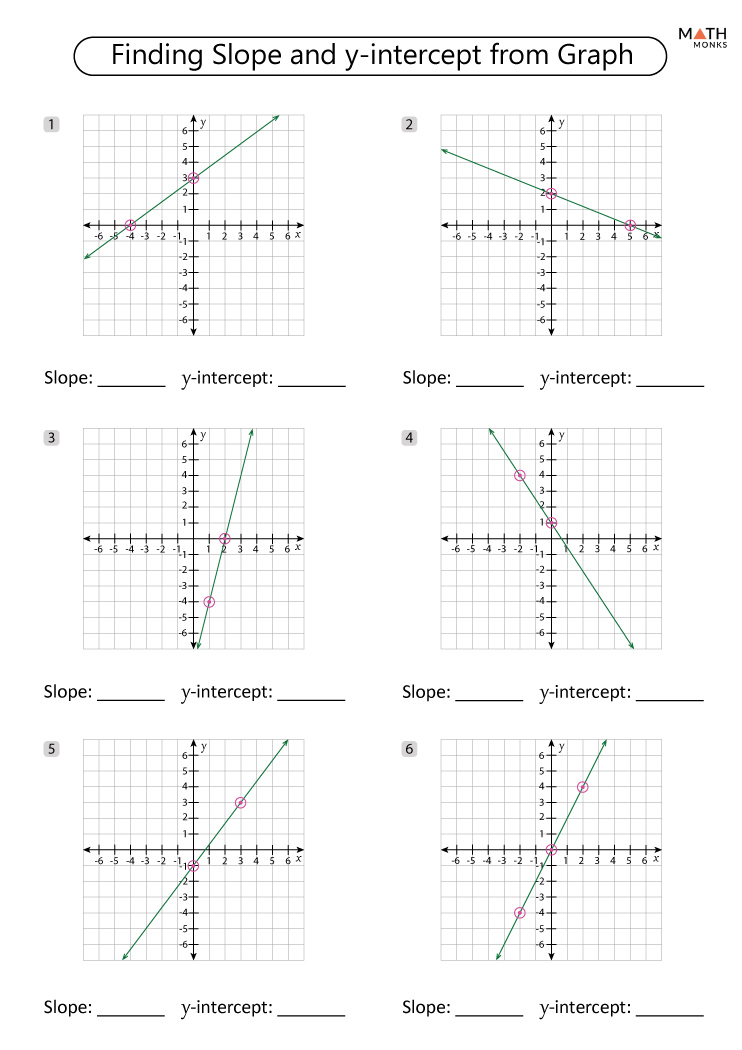
Are you keen on mastering the slope-intercept form of a line, an essential part of algebra and graphing? This blog post will guide you through using a slope-intercept worksheet to strengthen your mathematical understanding. Here's what you need to know to make the most of your practice sessions:
What Is Slope-Intercept Form?
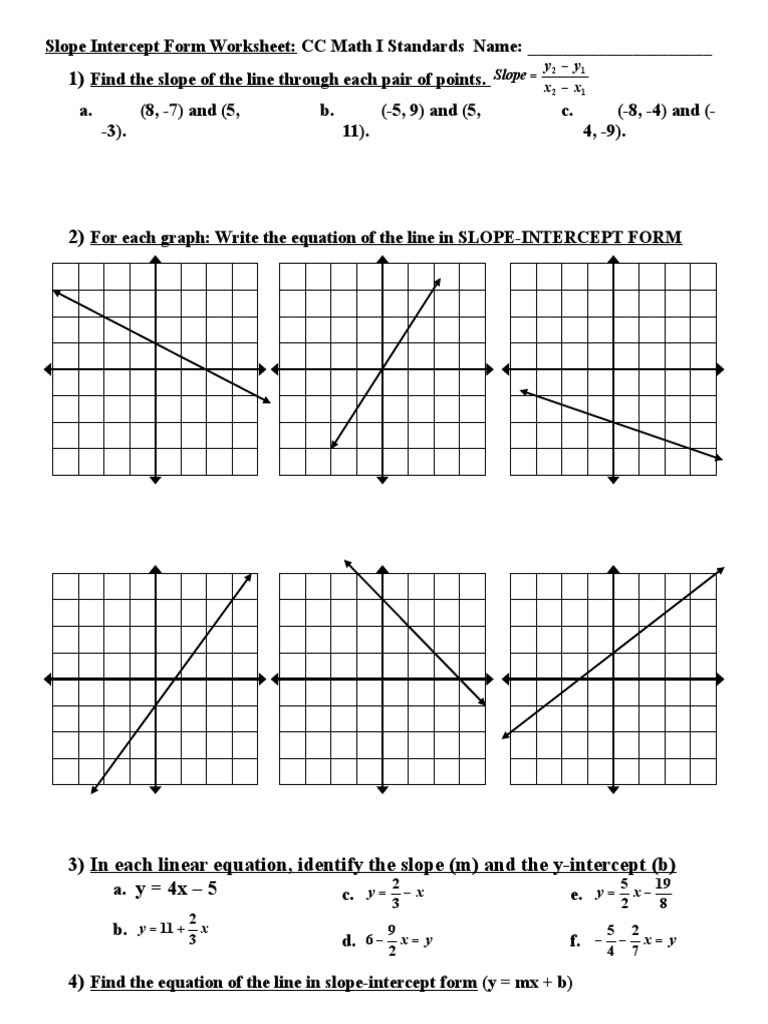
Slope-intercept form is a way to express the equation of a line in algebra. It's formatted as:
[ y = mx + b ]
- m - The slope of the line, which indicates its steepness and direction.
- b - The y-intercept, the point at which the line crosses the y-axis.
Why Use a Worksheet for Slope-Intercept Form?

Worksheets offer:
- Structured Practice - They help you approach problems systematically, enhancing your ability to recognize the form and convert equations.
- Visualization - Visual learners can benefit from graphing equations and seeing the lines take shape.
- Reinforcement - Repetitive practice ensures concepts are solidified in your memory.
How to Use a Slope-Intercept Worksheet

Here's a step-by-step guide to utilize your slope-intercept worksheet:
1. Understand the Basics
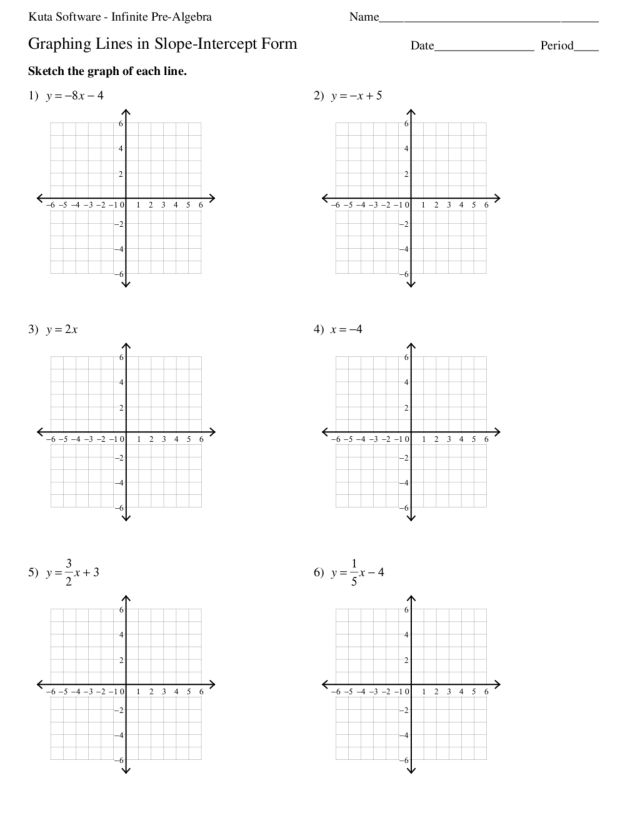
Before diving into exercises, make sure you grasp:
- How to calculate the slope between two points.
- Identifying the y-intercept from a graph or a given equation.
- Converting equations from other forms into slope-intercept form.
📝 Note: Start with simple problems and gradually work your way up to complex ones to build confidence and understanding.
2. Analyze Example Problems
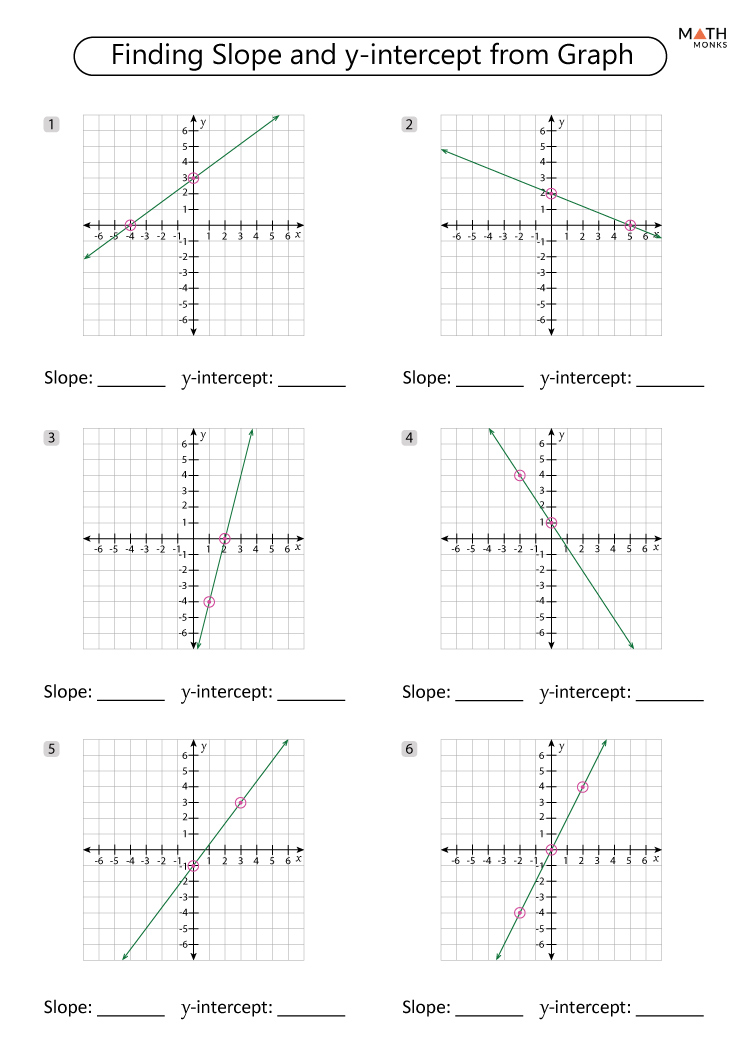
Your worksheet might come with examples or model problems. Pay attention to:
- The given information like points or slopes.
- The conversion process from another form into slope-intercept form.
| Given Problem | Step 1 | Step 2 | Result |
|---|---|---|---|
| Find equation given slope and point (2, 3) | Plug in the slope (m) | Plug in the point's x and y values | y = mx + b => y = 2x + b |

3. Work Through the Exercises

Now it's your turn:
- Solve problems where you're given the slope and a point.
- Convert equations from standard form or point-slope form to slope-intercept.
- Graph lines to check your answers visually.
📝 Note: Always check your work by plugging in the coordinates of points on the line to ensure your equation is correct.
4. Use Additional Features of the Worksheet

Many worksheets come with:
- Hints for stuck points.
- Extra practice for specific subtopics.
- Answer keys or explanations.
Common Pitfalls and How to Avoid Them

Here are some common mistakes students make:
- Incorrect Slope Calculation - Double-check your math when finding the slope.
- Negative Signs - Remember that negative slopes go downwards; ensure signs are correct.
- y-Intercept Confusion - Sometimes, the b term is not as straightforward as it seems; always isolate it.
In your practice sessions, you’ll encounter different scenarios to prepare for. Here are some final tips for using your worksheet effectively:
- Pace yourself, not rushing through problems but allowing time to process each step.
- Use a pencil; you can correct mistakes easily.
- Sketch quick graphs when necessary to visualize the line and check your work.
By incorporating these strategies and using your slope-intercept worksheet, you’ll elevate your ability to recognize, understand, and apply this fundamental algebra concept. Whether you’re solving for the slope, graphing equations, or converting line equations, you’ll be well-equipped to tackle any slope-intercept problem that comes your way.
Throughout your practice, keep your focus on the process, understanding each step, and don’t hesitate to return to the worksheet’s examples or resources when you need clarification. Remember, every problem is an opportunity to learn more, reinforce your skills, and gain mastery over this essential concept.
As you progress, consider these frequently asked questions for more insight:
What if I’m stuck on a problem?

+
Take a break, review the example problems or hints, and if needed, ask for help. Sometimes, reapproaching a problem with fresh eyes can lead to a breakthrough.
How can I remember the slope-intercept form?

+
Use mnemonics or visuals to remember ‘y = mx + b’. You can think of “m” as the ’m’ in “mountain”, indicating the slope or steepness, and ‘b’ as “beginning”, for where the line begins on the y-axis.
What if my answer is incorrect after graphing?

+
Review your calculations for errors in slope or intercept. Check your work for signs, decimal points, and ensure you’ve used the correct coordinates from the given points.
Is there a trick to quickly identify the slope and intercept?

+
Yes, look for the coefficient of x for the slope and the constant term for the y-intercept. Practice quickly rearranging equations to isolate these terms.
Can slope-intercept form be used for vertical or horizontal lines?

+
Vertical lines do not have a slope-intercept form as they have an undefined slope; their equation is in the form x = c. Horizontal lines have a slope of 0, so the form reduces to y = b.



