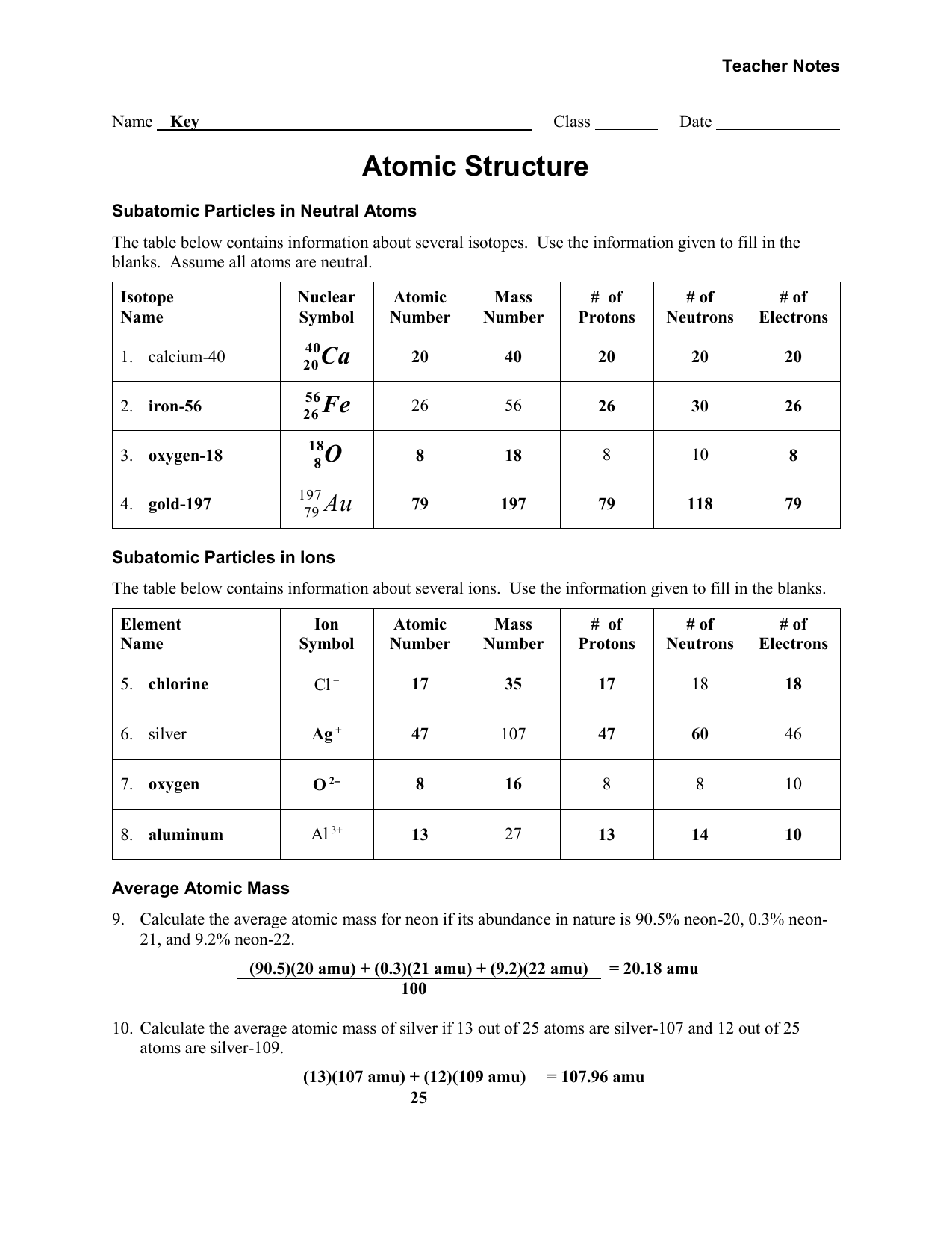
Dividing Fractions and Whole Numbers: Free Worksheet

Dividing fractions and whole numbers can often be perceived as a complex mathematical task, especially for students just beginning their journey into the realms of fraction manipulation. However, mastering this skill opens up a world of mathematical understanding that can be both fun and functional in daily life. This comprehensive guide is designed not only to clarify the division of fractions and whole numbers but also to provide you with a free worksheet to reinforce your learning through practice.
Understanding the Division of Fractions and Whole Numbers

Let’s start with the basics: what does dividing fractions really mean? When you divide one fraction by another or a fraction by a whole number, you are essentially asking how many of the second number fit into the first. Here’s how you do it:
- Divide a Fraction by a Whole Number: If you have a fraction ( \frac{a}{b} ) and you want to divide by ( c ) where ( c ) is a whole number, you can treat ( c ) as the fraction ( \frac{c}{1} ). Then, the operation changes to multiplying by its reciprocal: ( \frac{a}{b} \div \frac{c}{1} ) turns into ( \frac{a}{b} \times \frac{1}{c} ).
- Divide a Whole Number by a Fraction: When dividing a whole number ( w ) by a fraction ( \frac{d}{e} ), you multiply ( w ) by the reciprocal of the fraction: ( w \div \frac{d}{e} ) = ( w \times \frac{e}{d} ).
Step-by-Step Guide to Dividing Fractions by Whole Numbers

Here’s how you can divide a fraction by a whole number in simple steps:
- Write the Problem: Start with the fraction you wish to divide, then write the division sign followed by the whole number.
- Convert the Whole Number: Remember that any whole number ( c ) can be written as ( \frac{c}{1} ).
- Invert and Multiply: Instead of dividing, multiply your fraction by the reciprocal of the whole number.
- Simplify the Result: If possible, simplify the resulting fraction.
Practical Examples

Let’s work through some examples to see how this plays out in practice:
- Example 1: ( \frac{3}{4} \div 2 )
- Write the problem: ( \frac{3}{4} \div 2 )
- Convert the whole number: ( 2 ) becomes ( \frac{2}{1} ).
- Invert and multiply: ( \frac{3}{4} \times \frac{1}{2} = \frac{3 \times 1}{4 \times 2} = \frac{3}{8} ).
- Example 2: ( 5 \div \frac{2}{3} )
- Write the problem: ( 5 \div \frac{2}{3} )
- Invert the fraction: ( \frac{3}{2} ).
- Multiply: ( 5 \times \frac{3}{2} = \frac{5 \times 3}{1 \times 2} = \frac{15}{2} ).
- Simplify: ( \frac{15}{2} = 7 \frac{1}{2} ).
Why is Dividing Fractions Important?

The process of dividing fractions is crucial for several reasons:
- Practical Application: It’s used in real-life scenarios like dividing ingredients for recipes or scaling down measurements.
- Mathematical Foundation: Understanding how to divide fractions lays the groundwork for more advanced algebra and calculus concepts.
- Problem Solving: Division of fractions sharpens your ability to think logically and critically in solving complex math problems.
Downloadable Worksheet

We’ve prepared a free downloadable worksheet for you to practice dividing fractions and whole numbers. This worksheet includes:
- Basic problems to start.
- Intermediate questions to challenge your understanding.
- Advanced exercises for those looking to test their skills further.
📝 Note: Remember to simplify your answers where possible for optimal learning.
| Question Number | Problem | Answer |
|---|---|---|
| 1 | \frac{3}{4} \div 5 | \frac{3}{20} |
| 2 | 9 \div \frac{1}{3} | 27 |

📝 Note: You can print the worksheet or work on it digitally, depending on your preference.
As we've navigated through the process of dividing fractions by whole numbers and whole numbers by fractions, we hope you've gained not only the technical knowledge but also an appreciation for the practicality of this mathematical operation. Whether for practical applications, further mathematical education, or simply to sharpen your problem-solving skills, mastering this skill is undoubtedly beneficial. The downloadable worksheet will give you ample opportunity to practice, ensuring you can confidently tackle any problem involving fractions and whole numbers.
Why do we invert and multiply when dividing fractions?

+
The reason we invert (or flip) the second fraction and multiply is because division by a fraction is mathematically equivalent to multiplication by its reciprocal. This simplifies the operation into one that’s easier to perform and understand.
How do I know if my answer is correct after dividing fractions?

+
One effective way is to convert your answer back to the original division operation and perform the inverse calculation. If the original number is regained, your answer is likely correct.
Is there a visual way to understand dividing fractions by whole numbers?

+
Yes, imagine having a part of a pizza (fraction). Dividing this fraction by 2 means sharing that part equally among 2 people, which effectively gives you half of the original fraction again.