5 Essential Tips for Solving Slope Intercept Word Problems

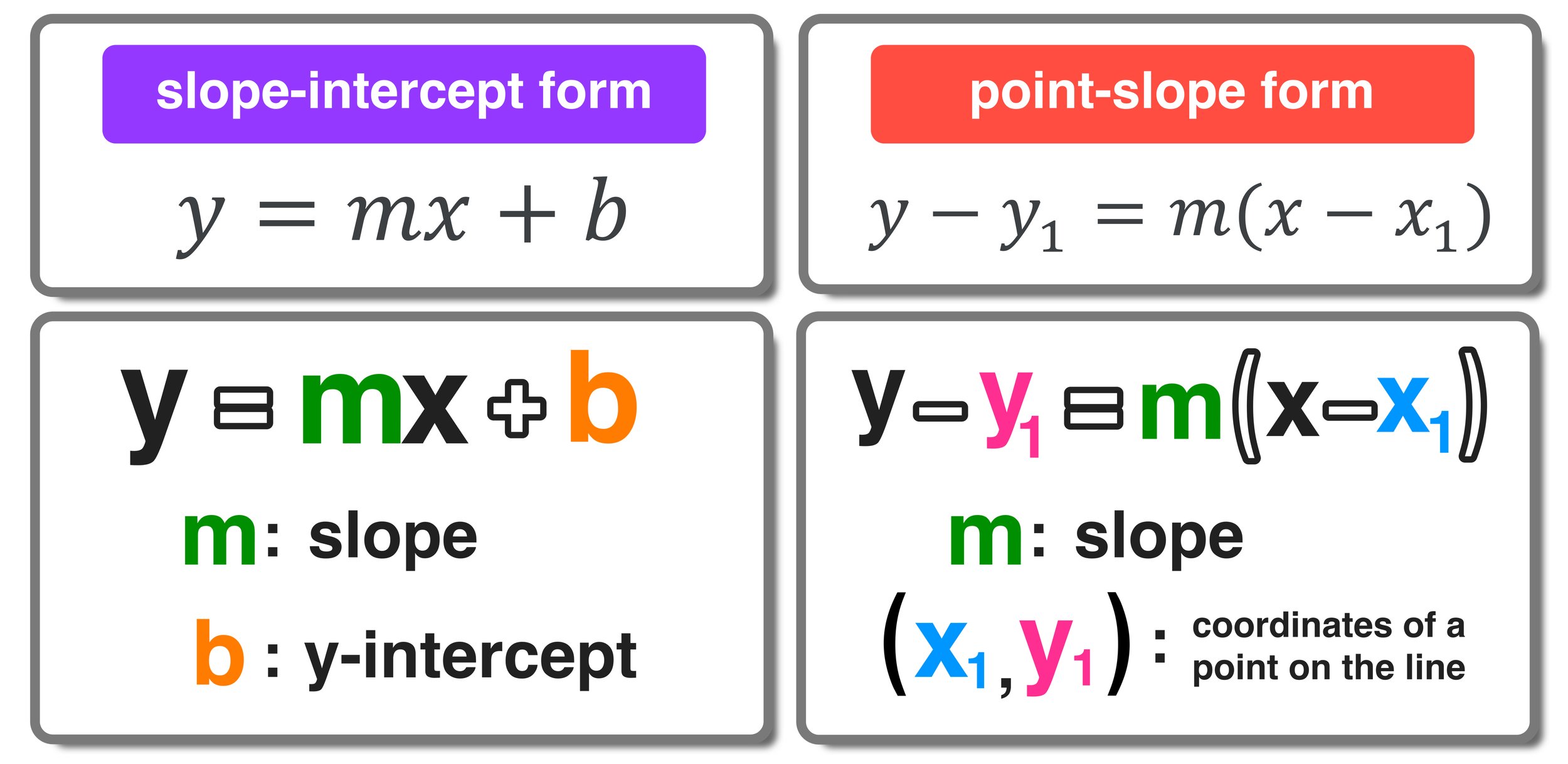
In the world of mathematics, particularly in algebra, one of the most common types of problems students encounter is solving word problems related to linear equations, especially those involving the slope intercept form. Slope intercept form, expressed as y = mx + b, where m is the slope of the line and b is the y-intercept, provides a structured way to understand and visualize linear relationships. Here, we're going to explore five essential tips that will help you master slope intercept word problems effectively.
Understand the Context


The first step in solving any word problem involving linear equations is to thoroughly understand the context given in the problem. Linear word problems often describe real-life scenarios that have linear relationships, like:
- The growth rate of a plant over time.
- The relationship between the cost of renting a car and the number of rental days.
- The profit made from selling a certain number of items.
Understanding the context means identifying the variables, determining the rate of change (which will become your m value), and recognizing any fixed values or initial conditions that will translate into the y-intercept, b.
Identify the Variables

In slope intercept form, x and y are your variables. Here are some steps to help you identify what these variables represent in word problems:
- Choose your variables: Assign x to the independent variable (often time or quantity), and y to the dependent variable (usually the result or outcome).
- Label clearly: Use specific labels to prevent confusion (e.g., ’t’ for time, ’d’ for distance).
- Look for relationships: Understand how one variable affects the other. The rate at which y changes when x changes is your slope, m.
Find the Slope

The slope, m, in a slope intercept equation is a crucial element. Here’s how you can find or derive the slope:
- Direct Rate: If the problem provides a direct rate of change (e.g., cost per item, speed), this value is your slope.
- Rate of Change Calculation: If the problem provides two points through which the line passes, you can calculate the slope using the formula: m = (y2 - y1)/(x2 - x1).
- Unit Analysis: Ensure units are consistent; for example, if distance is in miles and time in hours, your slope will have units like miles per hour.
Determine the Y-Intercept

The y-intercept, b, represents where the line crosses the y-axis or, in the context of the problem, the initial condition or fixed value:
- Starting Point: If the problem mentions a starting value or condition, that’s your y-intercept.
- Set x to zero: If you have the equation without the y-intercept, set x to 0 in the equation and solve for y.
💡 Note: The y-intercept doesn’t always represent a physical start point; it could be an abstract value in the problem’s context.
Solve and Interpret

Once you have your m and b, you can write the equation and use it to solve the word problem:
- Write the Equation: Combine the slope and y-intercept in the form y = mx + b.
- Substitute and Solve: Use the equation to find unknown values by plugging in the known x or y values.
- Interpret Results: Remember to interpret your results in the context of the problem. For example, if the problem involves profit, make sure to state the profit in dollars or units specified in the problem.
| Step | What to Do |
|---|---|
| 1 | Understand the Context |
| 2 | Identify Variables |
| 3 | Find the Slope |
| 4 | Determine the Y-Intercept |
| 5 | Solve and Interpret |
To summarize, mastering slope intercept word problems involves not only understanding the mathematical equations but also interpreting real-life scenarios correctly. By following these tips, you'll be able to solve these problems with confidence, ensuring that you understand the relationship between variables, can identify slope and y-intercept, and interpret the final results in context.
What is the significance of the slope in real-life problems?

+
The slope in real-life scenarios represents the rate of change or how one variable affects another. For example, in finance, it might represent the rate at which investments grow or debts decrease.
Can the y-intercept have a negative value?

+
Yes, the y-intercept can be negative, indicating that there’s an initial deficit, loss, or a starting point below the x-axis in the problem’s context.
How can I practice these word problems effectively?
+
Practice by solving a variety of problems from textbooks, online resources, or even creating your own scenarios. Focus on understanding the relationships and the context, not just on the math.