5 Ways to Master Slope Rate Change Worksheet

In the realm of education, particularly when teaching subjects like mathematics or science, worksheets are essential tools to gauge a student's understanding and proficiency. One such valuable worksheet focuses on the slope rate of change. Mastering slope rate change is not only pivotal for understanding foundational concepts in algebra but also applies across numerous disciplines where data analysis and interpretation are necessary. Here are five effective strategies to master the slope rate of change worksheet and enhance your comprehension of this critical mathematical concept.
1. Understand the Concept of Slope
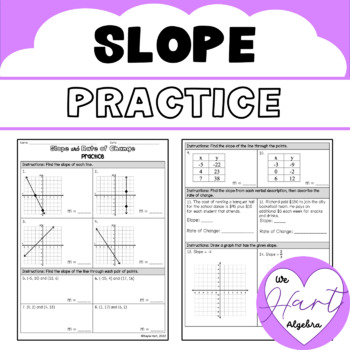

Before diving into any exercises, ensuring a firm grasp of what slope represents is crucial. Slope is defined as the ratio of the vertical change to the horizontal change between any two points on a line. It’s often described by the formula:
slope = (y2 - y1) / (x2 - x1)
- Vertical Change (Δy): The difference in y-coordinates.
- Horizontal Change (Δx): The difference in x-coordinates.
⚠️ Note: Understanding that slope measures steepness and direction is fundamental before proceeding with worksheets.
2. Develop Visual Recognition Skills

Utilizing visual aids can significantly aid in understanding slope. Here are some steps to develop this skill:
- Practice identifying slopes through graphs. Study how different slopes appear visually.
- Use graph paper to plot points and draw lines, allowing you to visualize the change in y as x changes.
- Observe how lines with different slopes behave when they intersect the axes.
Developing this skill allows you to quickly discern positive, negative, zero, and undefined slopes in graphical form, making worksheet exercises more intuitive.
3. Engage in Interactive Learning

Learning through interaction can significantly improve retention and understanding. Here’s how to incorporate interactive learning:
- Use online graphing calculators or software like GeoGebra to dynamically manipulate slopes and observe changes in real-time.
- Participate in group activities where members explain their methods of calculating slopes to each other.
- Utilize games or apps designed for educational purposes that involve calculating and comparing slopes.
🚀 Note: Interactive learning not only makes the process more enjoyable but also helps solidify conceptual understanding.
4. Work on Slope Rate of Change Problems Systematically

When working on slope rate change worksheets:
- Read the Problem Carefully: Understand what is being asked before jumping into calculations.
- Identify Points: Make sure to correctly identify the two points you will use to calculate the slope.
- Set Up the Equation: Arrange the coordinates into the slope formula.
- Calculate: Perform the subtraction and division as per the formula. Ensure to reduce fractions if necessary.
- Interpret: Understand what the slope value means in context (e.g., speed, rate of change, etc.)
| Steps | Example |
|---|---|
| Identify Points | (2, 3) and (4, 7) |
| Set Up Equation | slope = (7 - 3) / (4 - 2) |
| Calculate | slope = 4 / 2 = 2 |
| Interpret | The line rises 2 units for every 1 unit it moves to the right. |

5. Regular Practice and Feedback
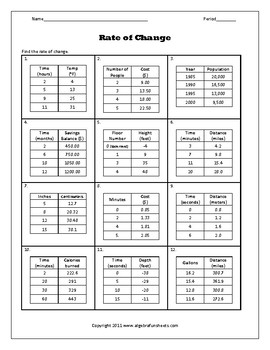
Consistent practice is the key to mastery:
- Complete at least one worksheet every few days, increasing the difficulty as your understanding improves.
- Seek feedback from peers or teachers to verify your work. Understanding where you make mistakes is crucial for improvement.
- Use online resources or textbooks to find additional problems if needed.
✅ Note: Regular practice, combined with constructive feedback, ensures steady progress in mastering slope rate of change.
In mastering the slope rate of change, it’s beneficial to approach the topic from multiple angles. By grasping the concept, visualizing slopes, engaging interactively, systematically solving problems, and practicing regularly, you can significantly enhance your proficiency. This holistic approach not only prepares you for worksheets but also equips you with a deeper understanding of how slope influences real-world applications in various fields. Remember, mastering any mathematical concept is a journey of continuous learning and application.
Why is understanding slope important?

+
Slope is crucial because it represents the rate of change between two variables. This understanding is vital in numerous fields like physics for calculating velocity, in finance for analyzing trends, and in everyday applications like interpreting graphs or maps.
How can I quickly check if my slope calculation is correct?

+
One quick check is to plot the points on a graph if possible. Draw a line through these points and see if it matches the slope value you’ve calculated. Also, ensure that the sign of the slope (positive, negative, zero, undefined) is logical given the context.
What if I encounter a slope that is infinite or undefined?

+
An undefined or infinite slope refers to a vertical line. This means that as the x-coordinate stays the same, the y-coordinate changes infinitely, making the slope division undefined (division by zero). In practical terms, this represents a situation where there is no change in one variable while the other changes drastically.