Sine Law and Cosine Law: Essential Worksheet Guide

Understanding the Sine Law and Cosine Law is crucial for students studying trigonometry, geometry, or calculus. These laws are foundational tools for solving problems related to triangles, particularly when dealing with unknown sides or angles in non-right triangles. This guide will walk you through how to apply these laws effectively, providing you with a comprehensive understanding through step-by-step explanations, examples, and practice problems.
The Sine Law

The Sine Law, or Law of Sines, states that in any triangle, the ratio of the length of a side to the sine of its opposite angle is constant. Mathematically, it can be expressed as:
sin(A)/a = sin(B)/b = sin(C)/c
When to Use the Sine Law

- When you know the measures of two angles and one side: If you have the lengths of sides A and B and need to find angle C, or if you know angles A and B and need to find side c, use the Sine Law.
- Ambiguous case: When you have one angle, its opposite side, and another side, there could be two possible triangles or no triangle at all. This scenario is known as the ambiguous case.
Example Using Sine Law
Let’s say we have a triangle where:
- Angle A = 45°
- Angle B = 60°
- Side a = 5 cm
To find side b, we use the Sine Law:
sin(A)/a = sin(B)/b
sin(45°)/5 = sin(60°)/b
b = 5 * sin(60°) / sin(45°)
b ≈ 5 * 0.866 / 0.707 ≈ 6.12 cm
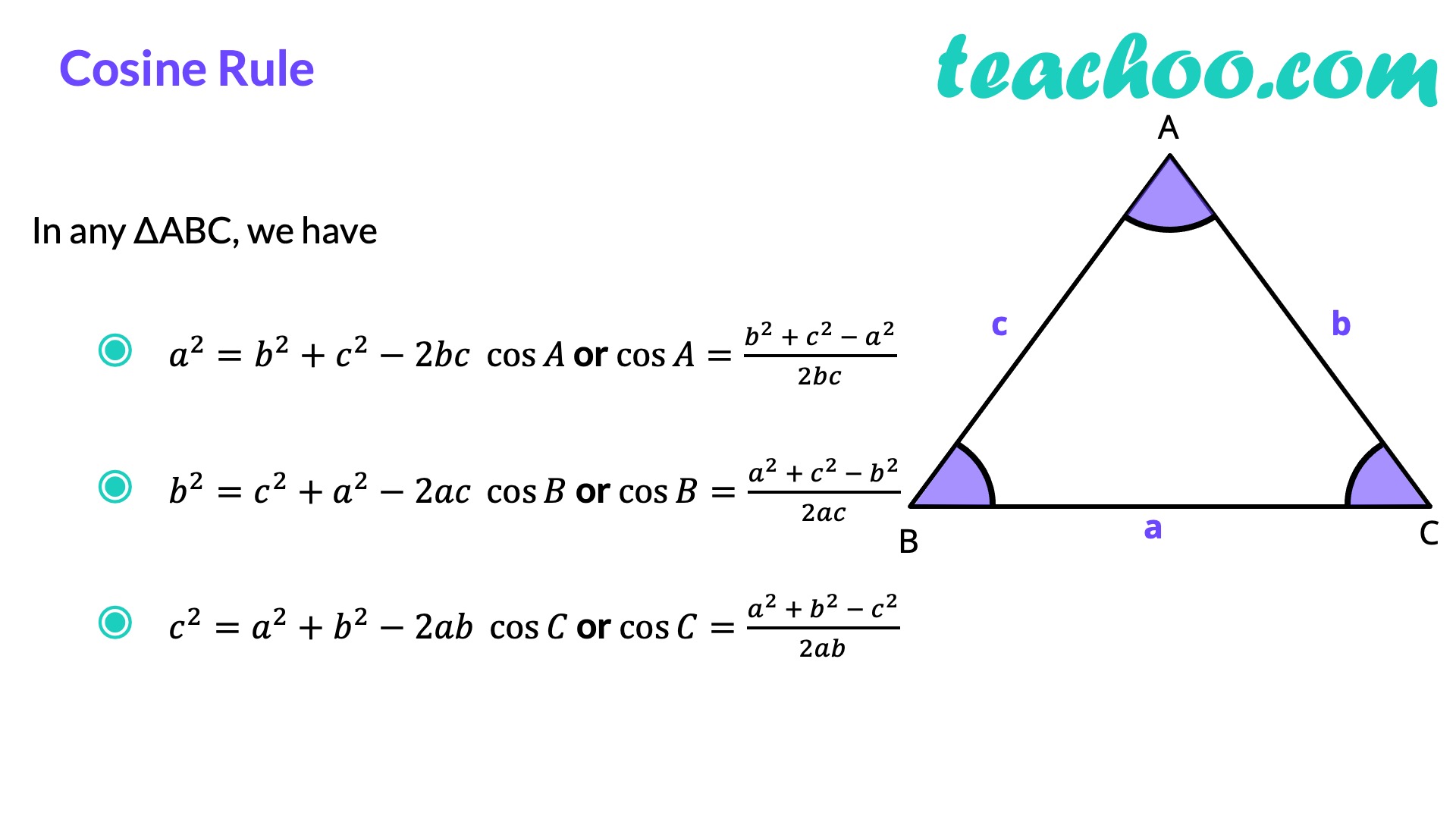
The Cosine Law

The Cosine Law, or Law of Cosines, provides a method to solve for sides or angles in any triangle. It’s especially useful in cases where three sides are known, or when two sides and the included angle are known. The formula is:
c² = a² + b² - 2ab * cos(C)
When to Use the Cosine Law

- When you know all three sides (SSS): To find an angle when all sides are known.
- When you know two sides and the included angle (SAS): To find the remaining sides or angles.
Example Using Cosine Law

Let’s consider a triangle where:
- Side a = 7 cm
- Side b = 8 cm
- Angle C = 110°
To find side c:
c² = a² + b² - 2ab * cos©
c² = 7² + 8² - 2 * 7 * 8 * cos(110°)
c² ≈ 49 + 64 - 2 * 56 * (-0.342) ≈ 147.148
c ≈ √147.148 ≈ 12.13 cm
Important Notes for Applying the Laws

📝 Note: Always check your angle measures. Remember, the sum of angles in any triangle must be 180°. This can be a helpful check to ensure your calculations are correct.
Worksheet Guide for Sine and Cosine Law

Here are some practice problems designed to help you master these laws:
| Problem Type | Description |
|---|---|
| Sine Law |
|
| Cosine Law |
|
| Ambiguous Case |
|

The key to mastering these laws is practice. Here are some steps to follow:
- Read through the problem carefully, identifying which law or laws you need to apply.
- Draw and label a diagram of the triangle if one is not provided.
- Apply the relevant law and solve for the unknown variable.
- Always check your results by verifying that the sum of angles is 180° or using the other law as a secondary check.
By following this guide and practicing these worksheet problems, you'll gain confidence in using the Sine and Cosine Laws. Remember that these tools are not just for solving academic problems but are also fundamental in many real-world applications like architecture, surveying, and even navigation.
How do I know when to use the Sine Law instead of the Cosine Law?

+
Use the Sine Law when you know two angles and one side (AAS, ASA) or when dealing with the ambiguous case (SSA). Use the Cosine Law when you know three sides (SSS) or two sides and the included angle (SAS).
What is the ambiguous case in the Sine Law?

+
The ambiguous case occurs when you know one angle, its opposite side, and another side (SSA). Here, you might get no solution, one solution, or two solutions depending on the triangle's configuration.
Can I solve a triangle using both laws?

+
Yes, in many cases, you'll need to use both laws in sequence to solve for all unknown sides and angles. For instance, you might use the Cosine Law to find one side, then the Sine Law to find an angle or another side.
Understanding and applying the Sine Law and Cosine Law can open up a multitude of problem-solving possibilities in trigonometry. With this guide, you are now equipped to handle a wide range of triangle problems, from the simplest to the most complex. Keep practicing, and soon these laws will become second nature, allowing you to analyze triangles with both precision and efficiency.



