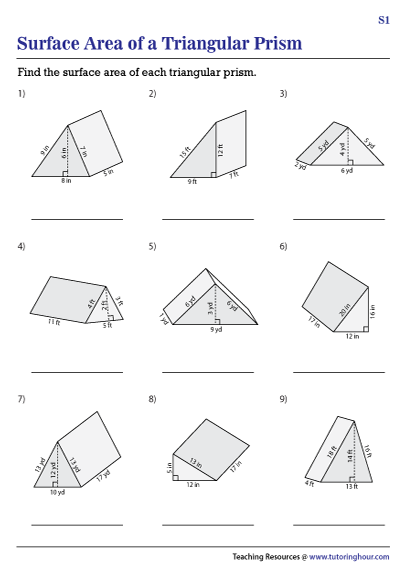
Triangle Similarity Worksheet: Master Geometry with Ease
Welcome to a comprehensive guide on triangle similarity, a cornerstone of Euclidean geometry that can unlock the secrets of many geometric problems and applications. Understanding triangle similarity not only allows you to solve complex geometric questions with ease but also lays a strong foundation for more advanced mathematical concepts. In this post, we will delve deep into the fundamentals of triangle similarity, explore the criteria for establishing when triangles are similar, and offer practical methods and worksheets to master this topic.
The Basics of Triangle Similarity

Triangle similarity refers to a condition where two triangles have the same shape, but not necessarily the same size. This principle is critical in geometry as it forms the basis for many proofs and geometric constructions. Here are the foundational ideas:
- Similar Triangles: Triangles that have their corresponding angles equal and their corresponding sides in proportion.
- Scaling: When one triangle is a scaled version of another, they are similar.
Criteria for Proving Similarity

There are several methods to prove that triangles are similar:
| Theorem | Description |
|---|---|
| Angle-Angle (AA) Similarity Postulate | If two angles of one triangle are equal to two angles of another triangle, the triangles are similar. |
| Side-Side-Side (SSS) Similarity Theorem | If the ratios of the corresponding sides of two triangles are equal, then the triangles are similar. |
| Side-Angle-Side (SAS) Similarity Theorem | If an angle of one triangle is equal to an angle of another triangle and the sides including these angles are proportional, then the triangles are similar. |
| Right Triangle Similarity Theorems | Includes Hypotenuse-Leg (HL), where if the hypotenuse and one leg of a right triangle are congruent to those in another, the triangles are similar. |

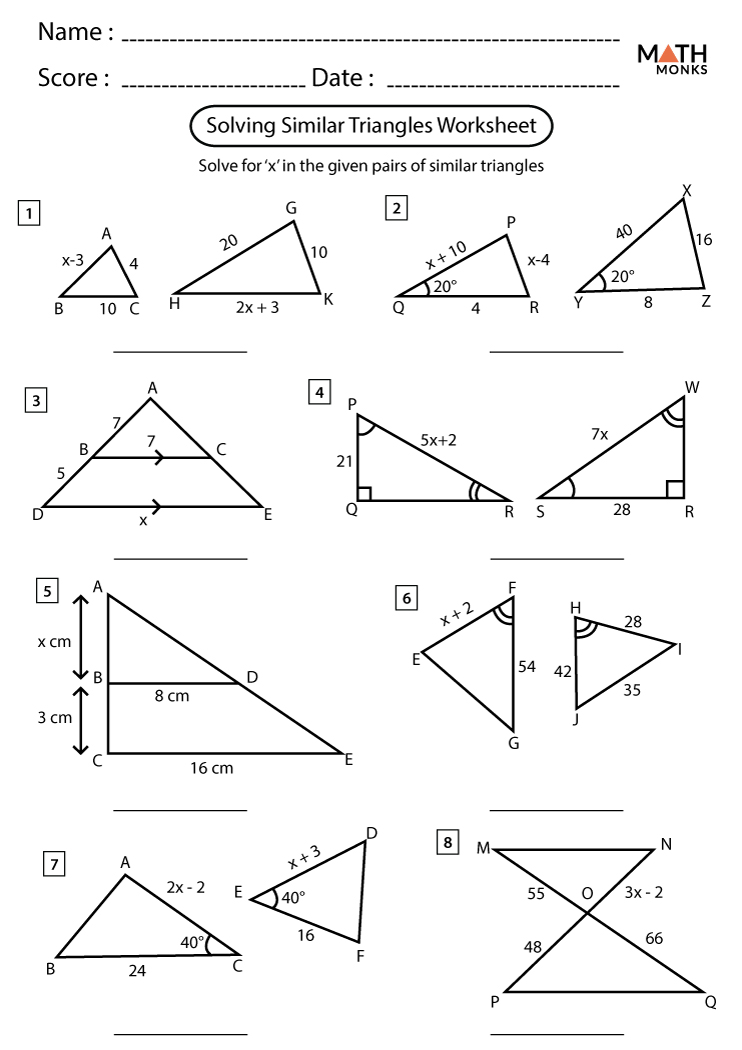
Understanding the Similar Triangle Worksheets

Triangle similarity worksheets are designed to reinforce your understanding through practice. Here’s how you can use them effectively:
- Identify Similarity Conditions: Use exercises that ask you to determine if triangles are similar based on given conditions.
- Proportion Calculation: Solve for missing sides or angles in similar triangles using the properties of proportions.
- Real-World Applications: Apply triangle similarity in solving problems related to shadows, building heights, and map scales.
Practical Tips for Solving Triangle Similarity Problems

Here are some strategies to enhance your problem-solving skills in triangle similarity:
- Use Diagrams: Always draw diagrams if none are provided to visualize the problem.
- Label Clearly: Label angles, sides, and proportions to avoid confusion.
- Understand Each Postulate: Know the conditions under which each similarity theorem applies.
- Practice with Different Approaches: Try solving a problem using different similarity postulates to get a deeper understanding.
🔍 Note: Remember to use geometric notation correctly, especially when working with symbols like '≈' for similar triangles and '∼' for corresponding sides in proportion.
Common Pitfalls and How to Overcome Them
Here are some common mistakes students make and how to avoid them:
- Incorrect Application of Theorems: Ensure you’re applying the right similarity theorem for the given information.
- Proportion Miscalculation: Always check your proportions by cross-multiplying.
- Overlooking Similar Triangles: Sometimes, triangles within a problem might not look similar but actually are, so pay attention to angles and proportions.
- Ignoring Congruence: Similar triangles can also be congruent, which means they’re not just similar but also have equal side lengths.
Enhancing Your Geometry Skills

Here are some additional steps to take your understanding of triangle similarity to the next level:
- Explore Advanced Theorems: Look into theorems like the Mean Proportionality Theorem or explore how similar triangles relate to areas and volumes.
- Project Work: Engage in geometry projects that involve designing or solving real-world problems using similar triangles.
- Peer Discussions: Discussing problems with peers can uncover new perspectives or approaches.
Triangle similarity is a fascinating and versatile topic in geometry that not only prepares you for further mathematical studies but also has practical applications in many fields, including architecture, engineering, and visual arts. Through the detailed exploration of similarity criteria, effective use of worksheets, and practical problem-solving strategies, you can master this subject with ease.
What are the key differences between similarity and congruence in triangles?

+
While both terms indicate some kind of equivalence between triangles, similarity refers to triangles having the same shape but potentially different sizes, where corresponding angles are equal and side lengths are proportional. Congruence, on the other hand, means that two triangles are not only similar but also have all corresponding sides equal in length.
Can two triangles be similar if they have one pair of angles equal?
+
No, having just one pair of angles equal does not guarantee similarity. To establish similarity, you must either have two pairs of corresponding angles equal (AA Postulate) or show that the sides are in proportion with at least one angle known.
How can you use similar triangles to measure indirect heights or distances?

+
Similar triangles can be used to measure heights or distances indirectly by setting up proportions. For example, if you know the height of a flagpole and the length of its shadow, you can use the angle of the sun to determine the height of a nearby tree by comparing the lengths of their shadows.
Why is understanding triangle similarity important?

+
Understanding triangle similarity is crucial because it:
- Helps in solving complex geometric proofs and problems.
- Is applied in real-world scenarios such as scaling, drawing, and designing.
- Forms the basis for understanding more advanced geometric concepts.
- Provides insights into trigonometric relationships and properties of shapes.