Similar Triangles Worksheet: Find Missing Sides Easily

When you dive into the world of geometry, understanding similar triangles and their applications is not just fun; it's essential. Similar triangles share the same shape, though not necessarily the same size, and this relationship enables us to solve for missing lengths efficiently. In this blog, we'll explore how to identify similar triangles, the methods to find missing sides, and some real-world applications of these geometric principles.
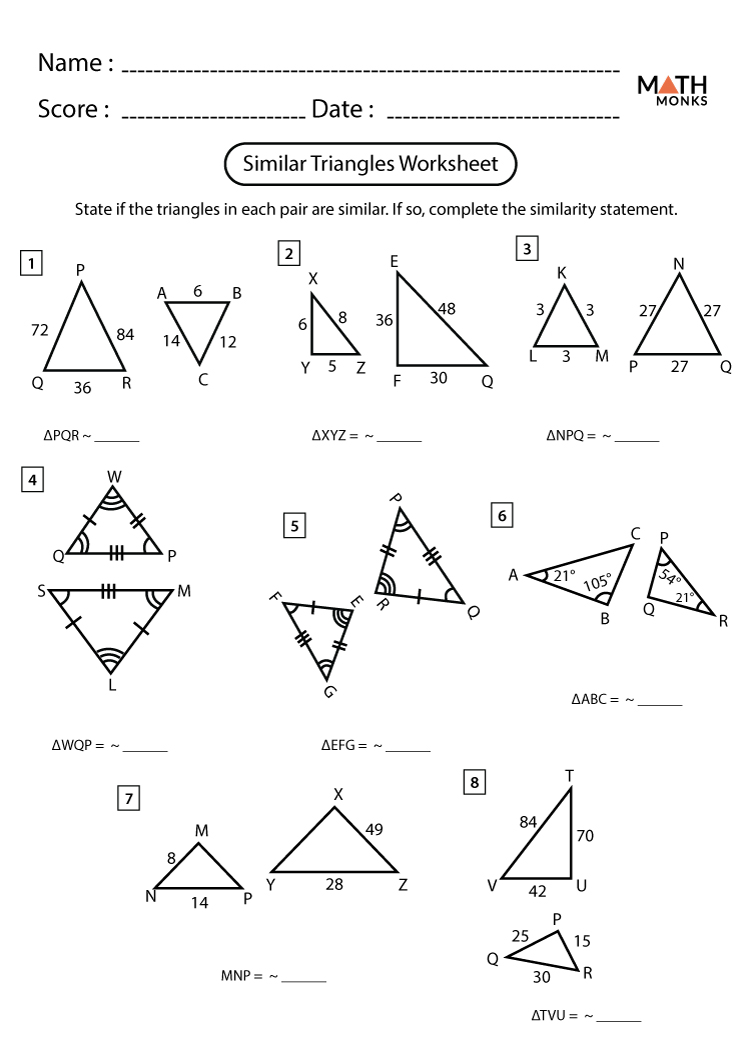
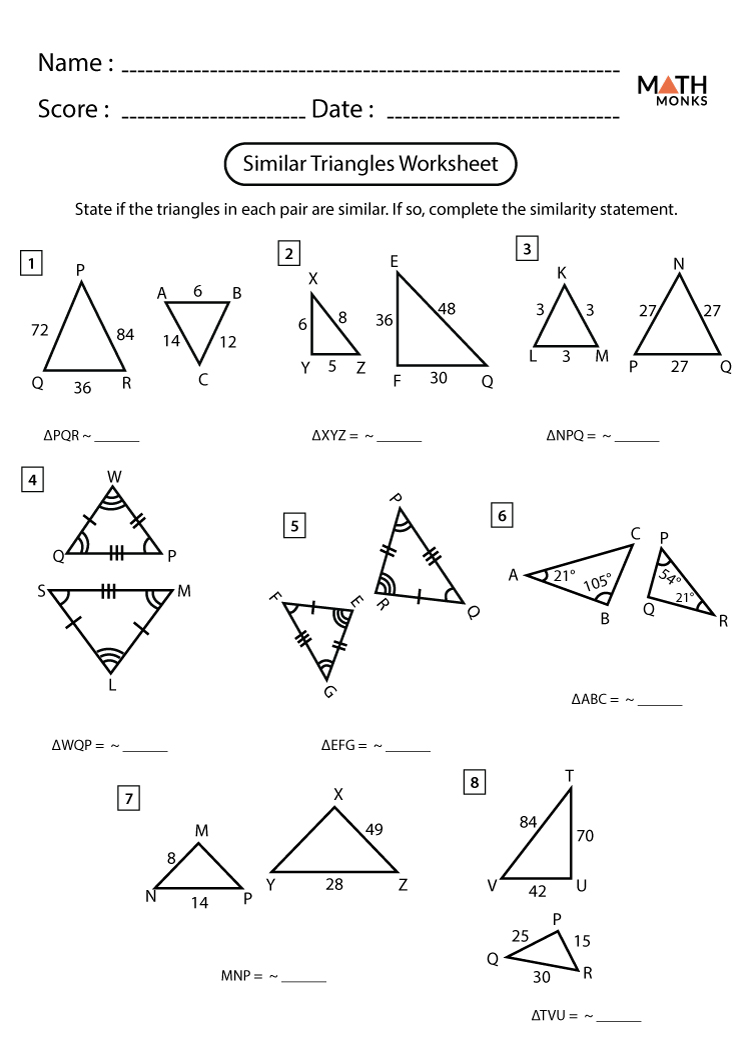
Identifying Similar Triangles

Before we can find missing sides, we need to recognize when triangles are similar. Here’s how:
- Angle-Angle (AA) Similarity Postulate: If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
- Side-Angle-Side (SAS) Similarity Theorem: When the ratios of two pairs of corresponding sides are equal, and the included angles are congruent, the triangles are similar.
- Side-Side-Side (SSS) Similarity Theorem: If the ratios of the three corresponding sides of two triangles are all equal, then the triangles are similar.
Finding Missing Sides in Similar Triangles
Once we’ve established that two triangles are similar, we can use this similarity to find missing side lengths. Here are the steps:
- Write Down the Proportion: Set up a proportion of corresponding sides using the ratio known sides from both triangles.
- Solve for the Unknown: Cross-multiply to solve for the unknown side, keeping the ratios consistent.
Example Problem:
| Triangle ABC | Triangle DEF |
|---|---|
| AB = 6 | DE = 4 |
| BC = 8 | EF = X (unknown) |
| CA = 5 | FD = 3 |

Setting up the proportion:
( \frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} )
Substituting in the known values:
( \frac{6}{4} = \frac{8}{X} )
Solving for X:
( 6X = 32 )
( X = \frac{32}{6} )
( X = 5.33 )
🔎 Note: Remember that similar triangles are proportionally enlarged or reduced versions of one another.
Real-Life Applications of Similar Triangles
Understanding how to use similar triangles to solve for unknown lengths isn’t just an academic exercise; it has practical applications:
- Photography and Film: Camera lenses use similar triangles to maintain perspective and focus on objects at different distances.
- Architecture: Architects use similarity principles to scale building designs from blueprints to real-world construction.
- Navigation and Astronomy: Mariners and astronomers use similar triangles to calculate distances or heights of celestial bodies.
Worksheet Practice:

Here’s a worksheet to practice finding missing sides in similar triangles:
- Problem 1: Given triangles PQR and STU where PQ=4, QR=6, PR=5, ST=2, SU=3. Find TU.
- Problem 2: Triangles DEF and JKL have sides DE=8, EF=12, DF=10, JK=6, JL=9. Find KL.
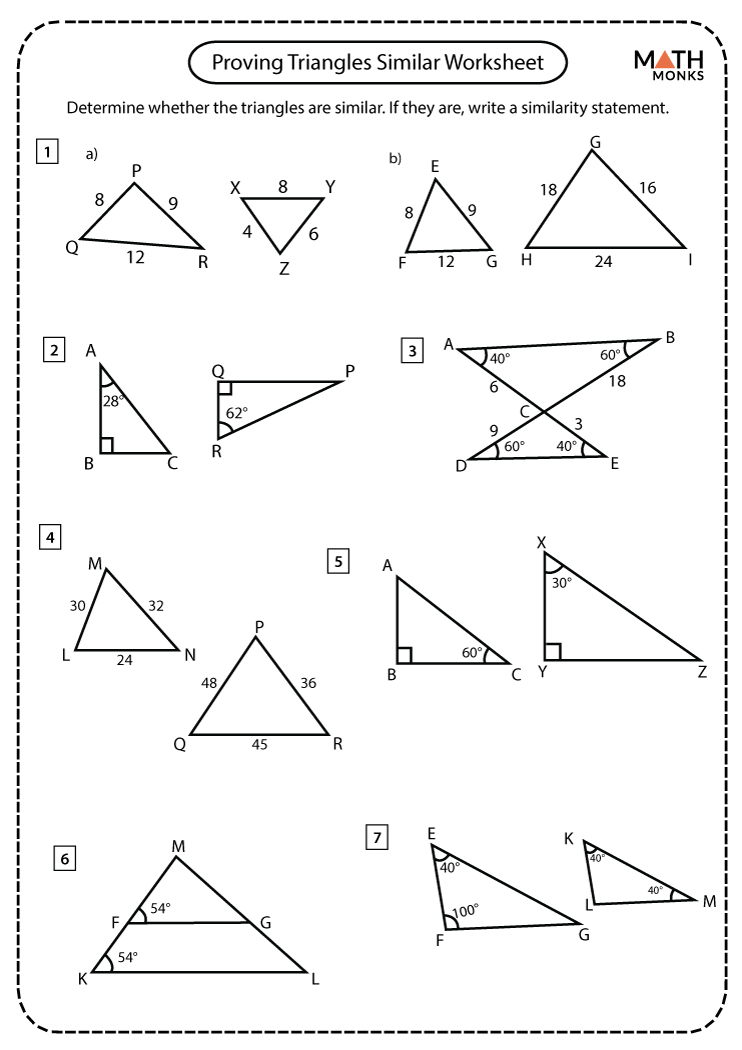
Common Pitfalls and Tips

- Watch Out for Scalars: Sometimes, a scalar multiple can be used to quickly find missing sides instead of setting up proportions.
- Correct Proportion Setup: Always ensure the corresponding sides of the triangles are correctly matched when setting up the proportion.
- Check Your Work: After solving for a missing side, check if the new side length adheres to the triangle inequality theorem (sum of the lengths of any two sides of a triangle must be greater than the length of the third side).
In geometry, particularly when dealing with similar triangles, mastering the ability to find missing sides can significantly enhance problem-solving skills and spatial understanding. This blog has provided insights into identifying similarity, solving for unknown sides using proportions, and highlighted some real-world applications of these concepts. Whether you’re a student, a hobbyist, or a professional, understanding similar triangles opens up a range of possibilities in both theoretical and practical mathematics.
What is the AA similarity postulate?

+
The Angle-Angle (AA) Similarity Postulate states that if two angles of one triangle are congruent to two angles of another triangle, then those triangles are similar.
How can I tell if two triangles are similar by their sides?

+
You can use the Side-Side-Side (SSS) or Side-Angle-Side (SAS) similarity theorems to determine if triangles are similar based on their sides.
Can similar triangles have different angles?
+
No, similar triangles have corresponding angles that are equal, although the triangles can vary in size.
What are some real-life examples of similar triangles?

+
Examples include shadows, maps or blueprints, photography, and architectural scaling. These all use the principles of similar triangles to represent or calculate distances and sizes.



