Similar Figures Worksheet Answers: Master Geometry Easily

Unlocking Geometry: A Deep Dive into Similar Figures

Geometry is a branch of mathematics that often intimidates students due to its abstract concepts and rigorous proofs. However, understanding similar figures can unlock a world of geometric understanding, making complex problems more approachable. In this comprehensive guide, we will explore how to:
- Identify similar figures
- Solve problems involving similar figures
- Utilize similarity in practical geometry scenarios
Understanding Similar Figures

Two figures are considered similar if they have the same shape but not necessarily the same size. This means:
- Angles are equal: Corresponding angles in similar figures are congruent.
- Proportional sides: The lengths of corresponding sides are in the same ratio.
Let’s delve into each of these properties:
Angles: - When two triangles or polygons are similar, all corresponding angles are equal. This is a crucial step in identifying similar figures.
Side Ratios: - The side lengths are proportional, which means you can express the lengths of one figure’s sides as a ratio to another’s. For example, if triangle ABC is similar to triangle DEF, then the ratio AB/DE = BC/EF = CA/FD.
How to Determine If Figures Are Similar

To determine if two figures are similar, follow these steps:
Check the Angles: Compare the angles between the figures. If all corresponding angles are congruent, the figures might be similar.
Verify Proportions: Measure the sides or given measurements. Calculate the ratio for at least two sides of one figure to corresponding sides of the other. If all ratios are equal, the figures are similar.
Look for AA, SSS, or SAS Similarity Postulates:
- AA (Angle-Angle) similarity: If two angles of one triangle are equal to two angles of another triangle, the triangles are similar.
- SSS (Side-Side-Side) similarity: All three sides of one triangle are proportional to the sides of the other triangle.
- SAS (Side-Angle-Side) similarity: If two sides of one triangle are proportional to two sides of another triangle and the included angles are equal, the triangles are similar.
Table of Similarity Postulates

| Postulate | Description |
|---|---|
| AA Similarity | If two angles of one triangle are equal to two angles of another triangle, the triangles are similar. |
| SSS Similarity | If all three sides of one triangle are proportional to the sides of another, the triangles are similar. |
| SAS Similarity | If two sides of one triangle are proportional to two sides of another triangle and the included angles are equal, the triangles are similar. |

Using Similar Figures in Geometry

Similarity plays a significant role in solving geometric problems:
- Finding Lengths: Once you establish similarity, you can find unknown lengths in figures by setting up proportions.
For example, if triangle ABC ~ triangle DEF and AB = 10 cm, BC = 15 cm, DE = 5 cm, find EF:
<p class="pro-note">🎓 Note: This setup allows you to find side lengths even when not all corresponding sides are given.</p>
- Area Ratios: The ratio of the areas of two similar figures is equal to the square of the ratio of their corresponding sides.
If the sides of one triangle are twice the sides of another similar triangle, the area of the larger triangle is 4 times that of the smaller triangle.
- Perimeter Ratios: The perimeter of similar figures relates to the ratio of their corresponding sides linearly.
Advanced Techniques in Solving Similar Figure Problems

For students looking to master geometry:
- Triangle Congruence: Understanding congruent triangles can help in similarity proofs.
- Proportional Reasoning: Apply proportional reasoning to find unknown dimensions or solve complex geometric puzzles.
- Similarity Transformations: Use transformations like dilations to create similar figures and solve problems involving their properties.
🎨 Note: Visual aids like drawing similar figures in different scales can help visualize these concepts.
As we wrap up our journey through the world of similar figures, it’s clear that these concepts are not just mathematical tools but a pathway to understanding more advanced geometric principles. From identifying figures based on angles and proportions to applying these concepts in real-world scenarios, mastering similar figures can significantly enhance your problem-solving skills in geometry.
This comprehensive understanding of similar figures:
- Enables easier solutions to geometry problems through proportional relationships
- Deepens your geometric intuition
- Prepares you for advanced geometric topics
Remember, the next time you encounter geometric shapes, whether in textbooks, architecture, or nature, look for those similar shapes to unlock the simplicity hidden in their complexity.
What is the difference between congruent and similar figures?

+
Congruent figures have the same size and shape, meaning they are identical in every way. Similar figures, on the other hand, share the same shape but can differ in size.
Can two polygons be similar if they are not regular?

+
Yes, as long as they have corresponding sides proportional and corresponding angles equal. Irregular polygons can still be similar if they meet these criteria.
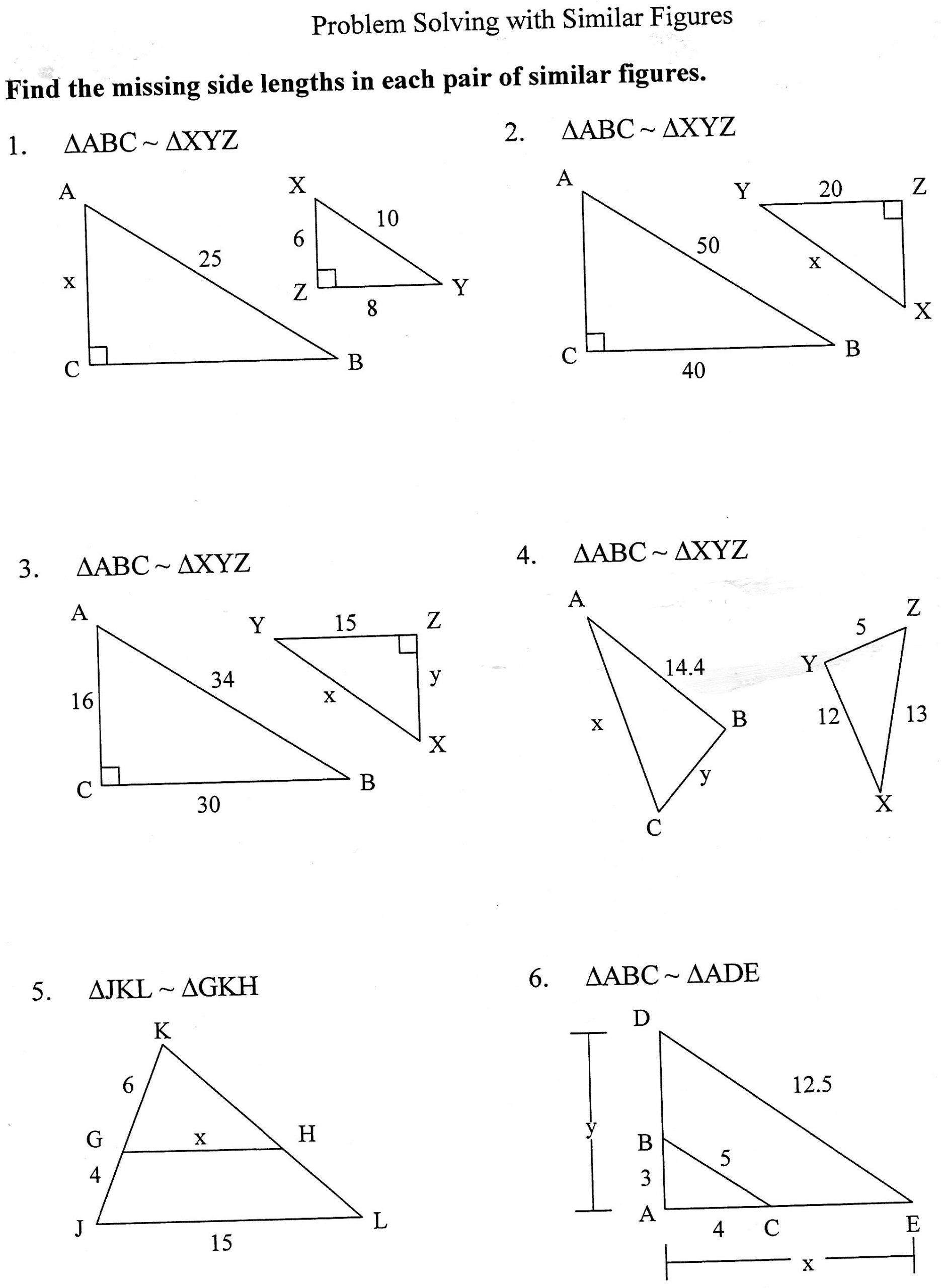
How do I solve for missing lengths in similar figures?
+
Set up a proportion between the corresponding sides of the similar figures. If you know three out of four side lengths, use the proportion to find the unknown length.
Related Terms:
- Similar figures Worksheet PDF
- Similar figures Worksheet Geometry