7 Proven Tips for Mastering Slope Graphing Worksheets
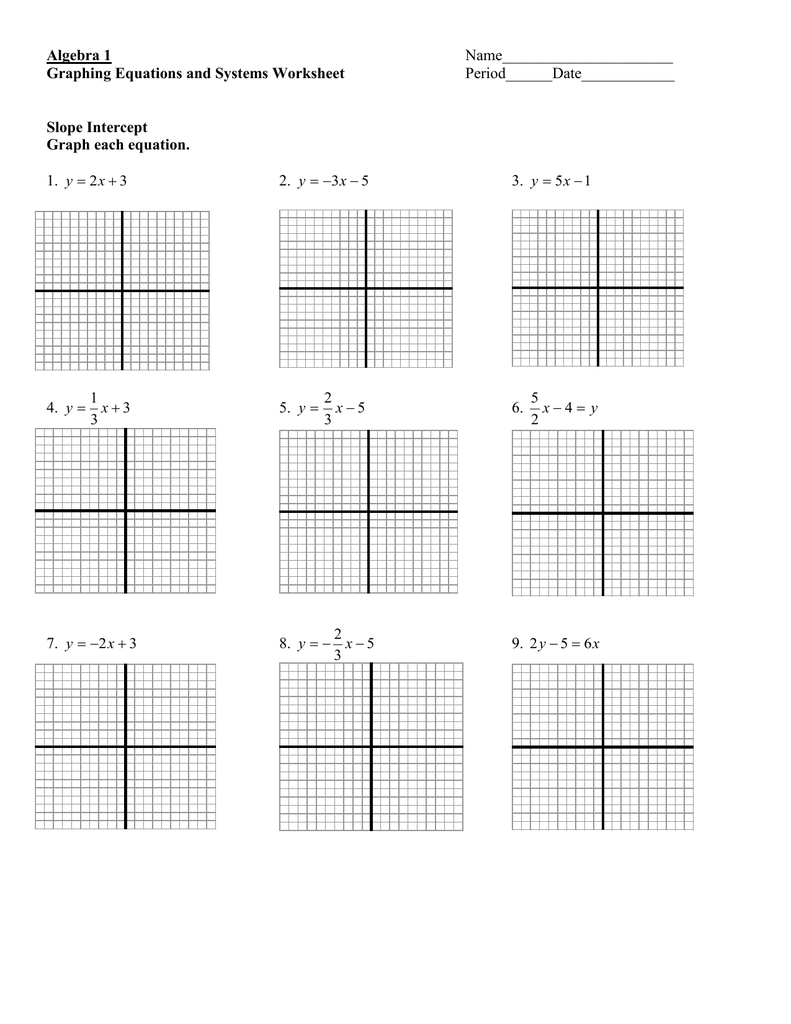
Understanding how to graph slopes on a worksheet can be incredibly useful, whether for students tackling algebra or data analysts visualizing trends. Slopes are fundamental in understanding relationships in data sets, and mastering slope graphing worksheets can provide a clearer insight into these relationships. Here are seven proven tips to help you become proficient in mastering slope graphing worksheets:
1. Understand the Basics of Slope

Before diving into graphing slopes, make sure you have a solid grasp of what slope represents. Slope is the measure of steepness of a line, often denoted as m in the equation y = mx + b, where m represents the slope and b the y-intercept:
- Positive Slope: The line rises from left to right.
- Negative Slope: The line falls from left to right.
- Zero Slope: The line is horizontal.
- Undefined Slope: The line is vertical.
2. Practice Plotting Points

Begin with simple exercises where you plot given points on a coordinate grid. This foundational skill is crucial for accurately drawing lines with specific slopes. Here’s how to approach it:
- Identify the coordinates for each point provided.
- Plot these points on the coordinate plane, using a pencil for ease of correction.
- Connect the points to form a line, and use this opportunity to understand how slopes behave.
3. Use Grid Lines to Your Advantage
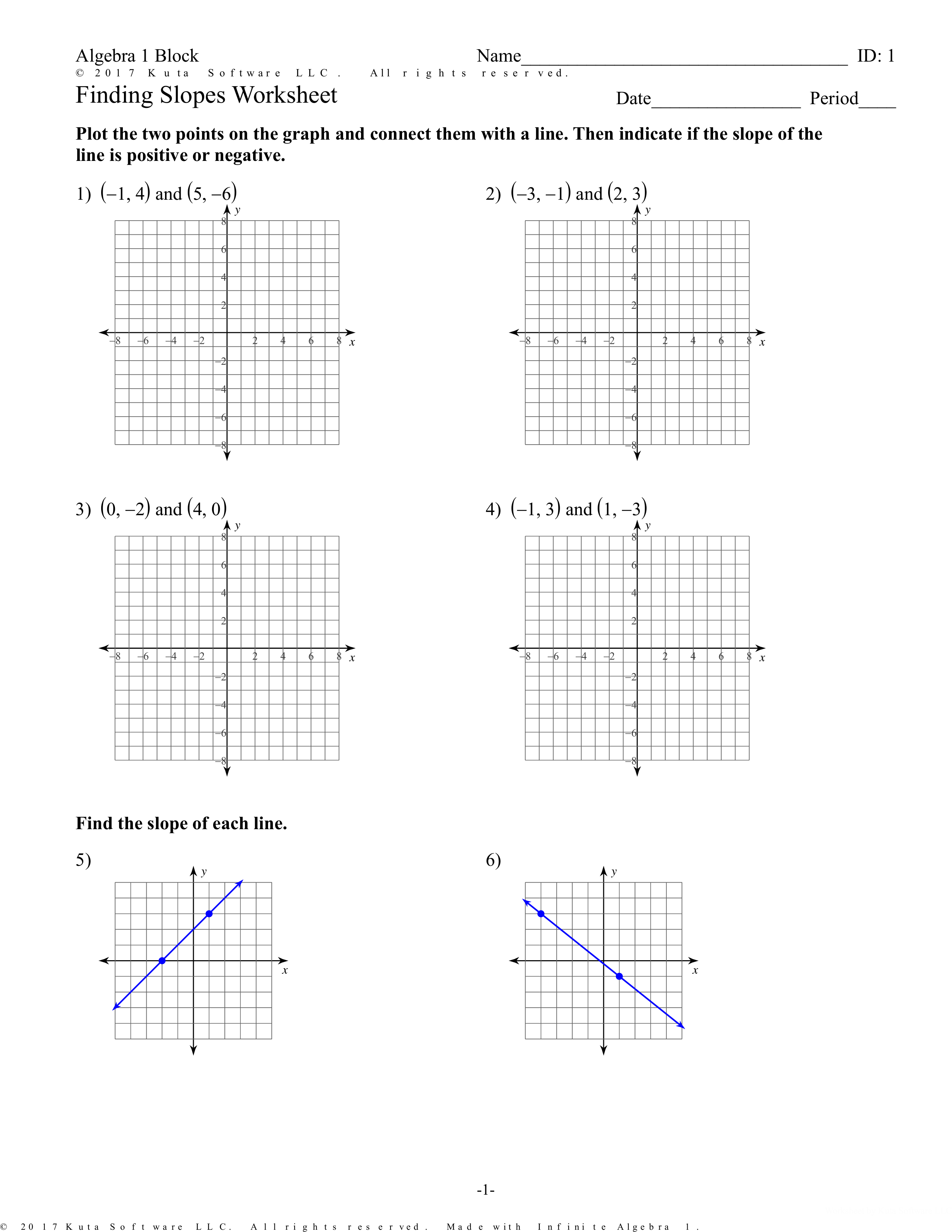
When working with slope graphing worksheets, always utilize the grid lines:
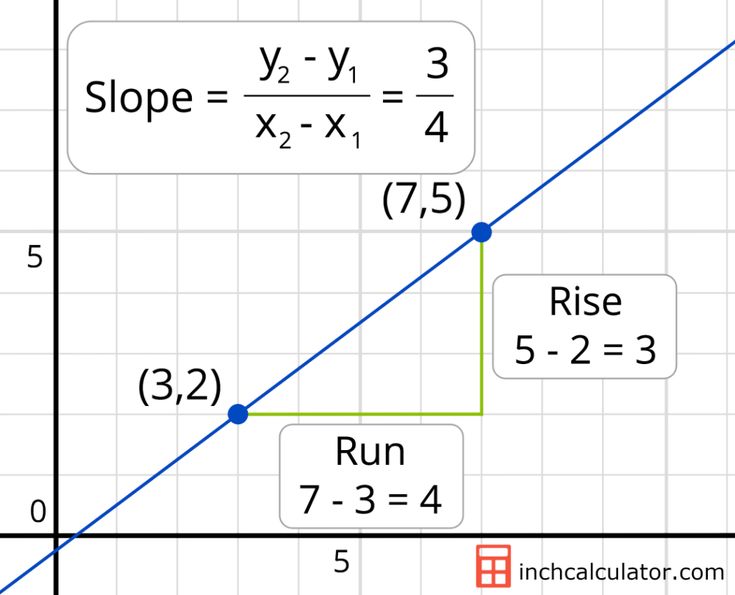
- Count the vertical distance (rise) and horizontal distance (run) between points to determine the slope.
- Sketch lines on graph paper, which allows for precise measurement.
4. Master the Slope-Intercept Form
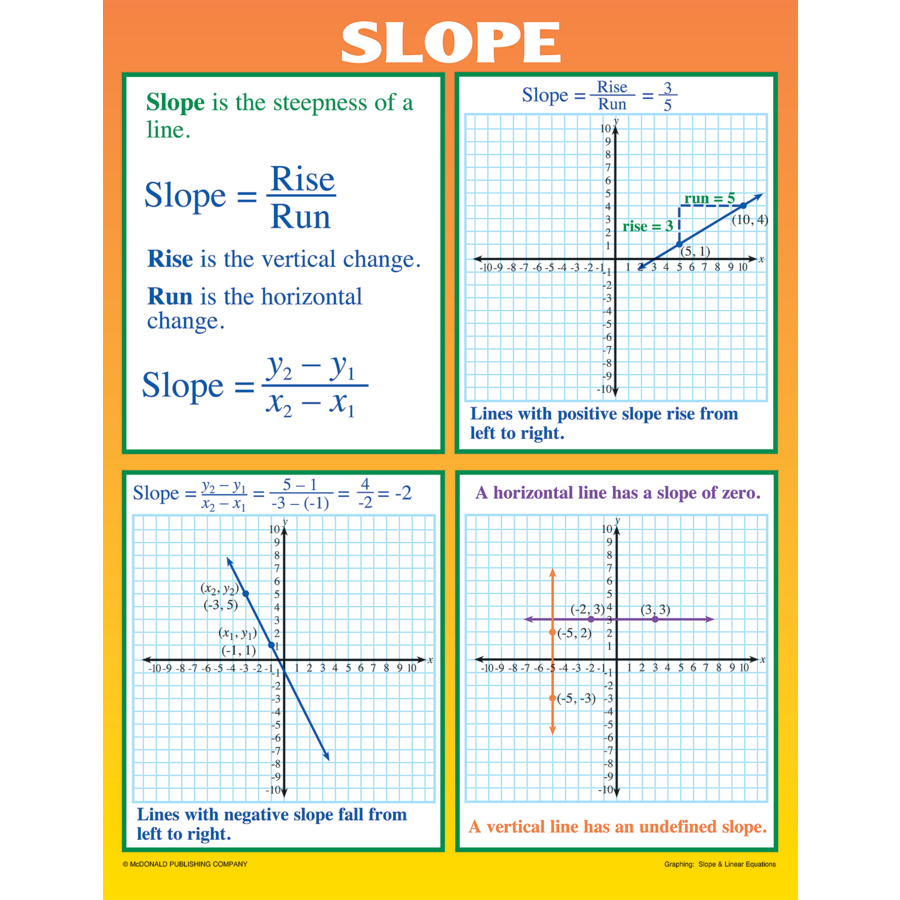
Becoming fluent in the slope-intercept form, y = mx + b, will significantly enhance your ability to graph slopes efficiently. Here’s what to focus on:
- m: Calculate the slope between two points.
- b: Locate the y-intercept by seeing where the line crosses the y-axis.
Here's a sample calculation:
| Point 1 | Point 2 | Slope (m) | Y-Intercept (b) |
|---|---|---|---|
| (2, 3) | (4, 7) | 2 (From (7-3)/(4-2)) | 1 (since line intersects y-axis at y=1) |

📝 Note: This equation form helps in directly plotting the y-intercept and then using the slope to find other points.
5. Visualize Slopes with Real-World Applications

Apply slope graphing to real-world scenarios to reinforce your understanding:
- Analyze ramps or stairs where the slope can represent the steepness.
- Look at economic trends, weather patterns, or any scenario where change over time is crucial.
6. Regularly Review and Practice

Repetition is key in mastering any skill:
- Work through different types of problems regularly.
- Use online resources or create flashcards with different slopes and their graphical representations.
7. Identify and Correct Common Mistakes
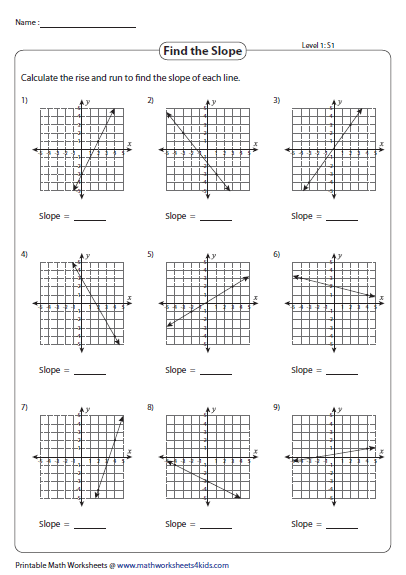
Common errors in slope graphing include:
- Confusing rise and run.
- Not considering the direction (positive or negative) of the slope.
- Inaccurate plotting of y-intercept or misreading the given coordinates.
⚠️ Note: If your line doesn’t pass through all given points, recheck your calculations for rise and run.
In wrapping up, mastering slope graphing worksheets involves a deep understanding of slope concepts, regular practice, and careful application of grid lines to ensure accuracy. By using these seven tips, you're setting yourself up for success not just in algebra or graphing worksheets, but in any scenario where understanding change over time or comparative analysis is needed. Whether you're in school, preparing for standardized tests, or simply interested in data visualization, these skills are universally beneficial.
What is slope and why is it important?

+
Slope refers to the steepness of a line or the ratio of vertical change to horizontal change. It’s essential for understanding how one variable changes with respect to another, making it crucial in fields like engineering, finance, and any area where data analysis is involved.
How can I remember whether the slope is positive or negative?
+
Associate the directions of movement on the graph with the slope signs: Up and to the right is positive slope, and down and to the right is negative slope. Remember that “rise over run” will yield a positive number if rise and run are in the same direction.
Why might my graph not pass through all given points?
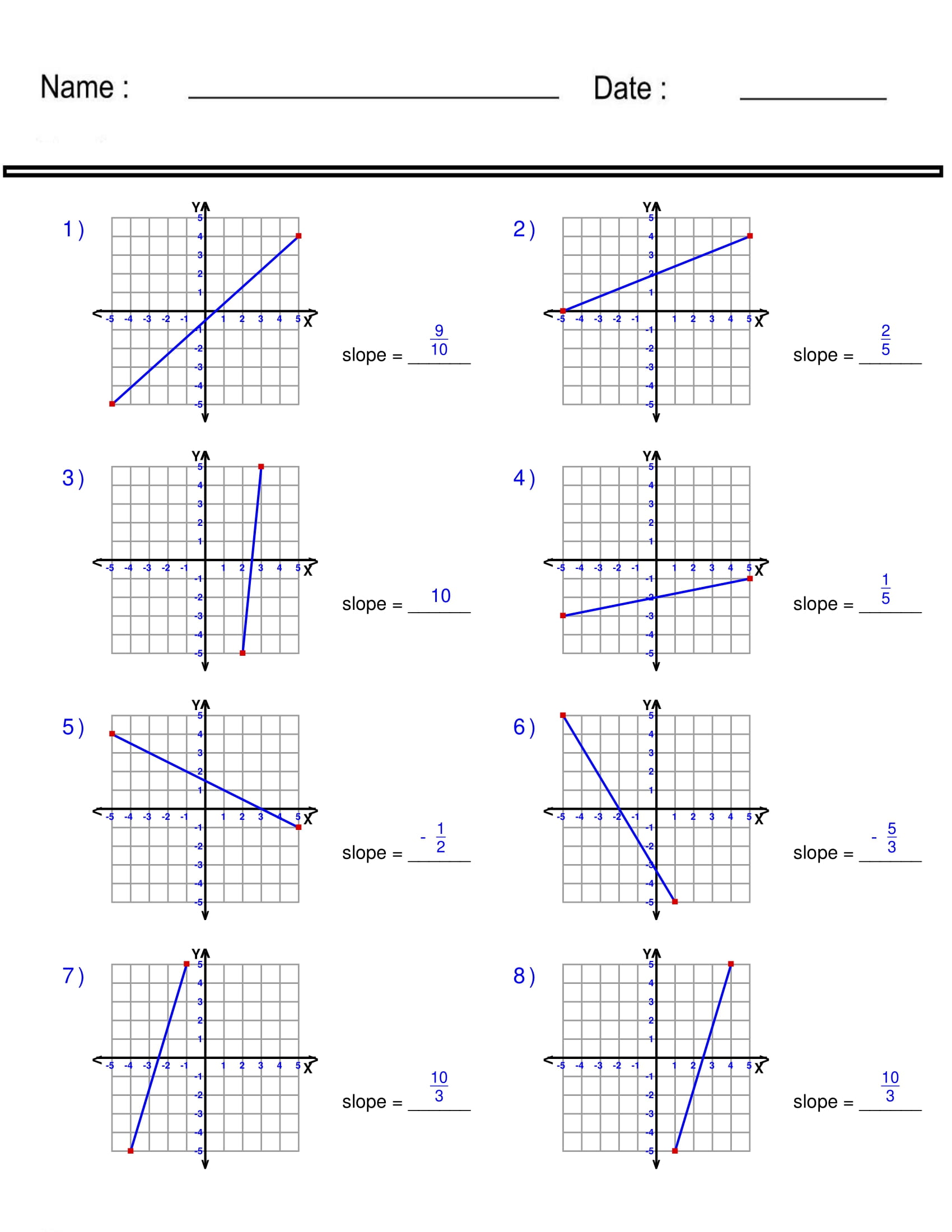
+
This usually indicates an error in calculating the slope, plotting the y-intercept, or plotting the points themselves. Recheck your work, ensuring accurate measurement of rise and run, and verify the coordinates of the points.
Can I use these tips for non-linear functions?

+
Yes, while these tips are designed for linear functions, the principles of slope, plotting, and understanding changes over time can apply to curves in calculus or data analysis. You’ll need to adapt your approach for finding slopes of tangents or understanding rate of change at specific points.



