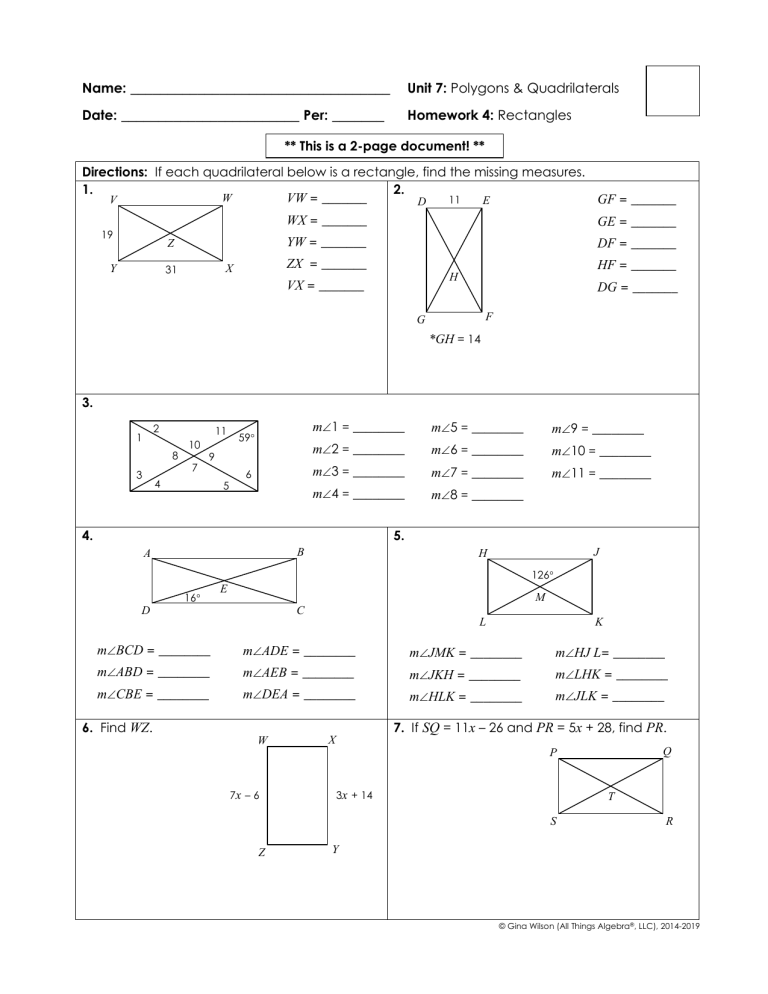
Similar and Congruent Figures Math Worksheet Mastery

Mastering similar and congruent figures in mathematics is crucial for students transitioning from basic geometry to more complex geometric concepts. Understanding these concepts not only aids in solving mathematical problems but also enriches one's appreciation of the symmetry and proportions found in real-world applications. This blog post will delve into:
- The definitions and differences between similar and congruent figures.
- Techniques for identifying and proving similarity and congruence.
- Applications of these concepts in real-life scenarios.
Understanding Similar and Congruent Figures
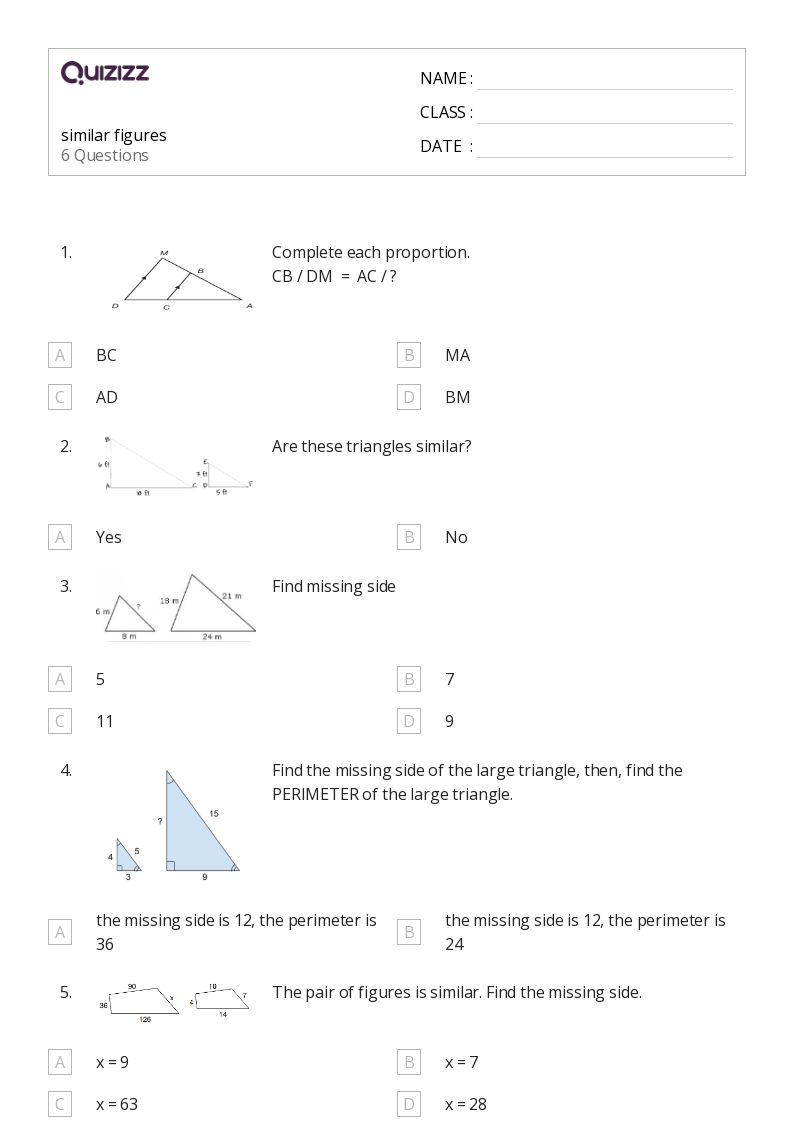
Similar figures are those that have the same shape but not necessarily the same size. This means their corresponding angles are equal, and their corresponding sides are proportional. In contrast, congruent figures have both the same shape and size; all their corresponding parts are identical in measure.
📏 Note: Congruence implies similarity, but similarity does not imply congruence.
Identifying Similar Figures

To identify if two figures are similar:
- Check Angles: All corresponding angles must be congruent.
- Compare Side Lengths: The ratios of corresponding sides must be constant.
- Use Proportions: Set up a ratio of corresponding sides to verify if they are in the same proportion.
Proving Similarity

There are several theorems used to prove similarity in triangles, which are fundamental for understanding similarity in more complex polygons:
| Theorem | Description |
|---|---|
| Angle-Angle (AA) Similarity Postulate | If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar. |
| Side-Angle-Side (SAS) Similarity Theorem | If an angle of one triangle is congruent to an angle of another triangle and the sides including these angles are proportional, then the triangles are similar. |
| Side-Side-Side (SSS) Similarity Theorem | If the lengths of corresponding sides of two triangles are proportional, then the triangles are similar. |

Identifying Congruent Figures

Identifying congruent figures involves:
- Direct Measurement: Measure corresponding parts to confirm they are identical.
- Using Congruence Postulates: Apply known postulates like:
- Side-Side-Side (SSS) Congruence Postulate
- Side-Angle-Side (SAS) Congruence Postulate
- Angle-Side-Angle (ASA) Congruence Postulate
- Angle-Angle-Side (AAS) Congruence Postulate
- Hypotenuse-Leg (HL) Congruence Theorem (for right triangles)
Applications in Real Life

Both similarity and congruence have practical applications:
- Architecture: Architects use scale models, which are similar to the actual buildings, to plan and visualize projects.
- Photography and Art: Proportions of objects can be changed using similarity to create visually appealing compositions.
- Navigation: Triangulation uses similar triangles to determine distances and locations.
- Machinery and Manufacturing: Parts need to be congruent to ensure they fit precisely together, maintaining the integrity of the machinery.
- Triangle Classification: Classify triangles by similarity or congruence using cutouts or software tools.
- Shadow Measurements: Use shadows to find heights or lengths of objects based on similar triangle properties.
- Scale Drawing: Create scale drawings of rooms or simple objects, ensuring accurate proportions.
- Congruent Shapes Puzzle: Cut out congruent shapes and reassemble them to form new figures, demonstrating congruence.
- Assuming that similar figures are congruent.
- Confusing the ratio of similarity with the scale factor.
- Not checking all angles or sides when proving similarity or congruence.
- Emphasize the difference between shape and size.
- Always use the scale factor or ratio correctly.
- Ensure that all necessary conditions for similarity or congruence are met.
📐 Note: Similarity can be used in photogrammetry to reconstruct dimensions from photographs.
Practical Exercises to Master Similarity and Congruence

Here are some hands-on exercises to enhance understanding:
Addressing Common Pitfalls
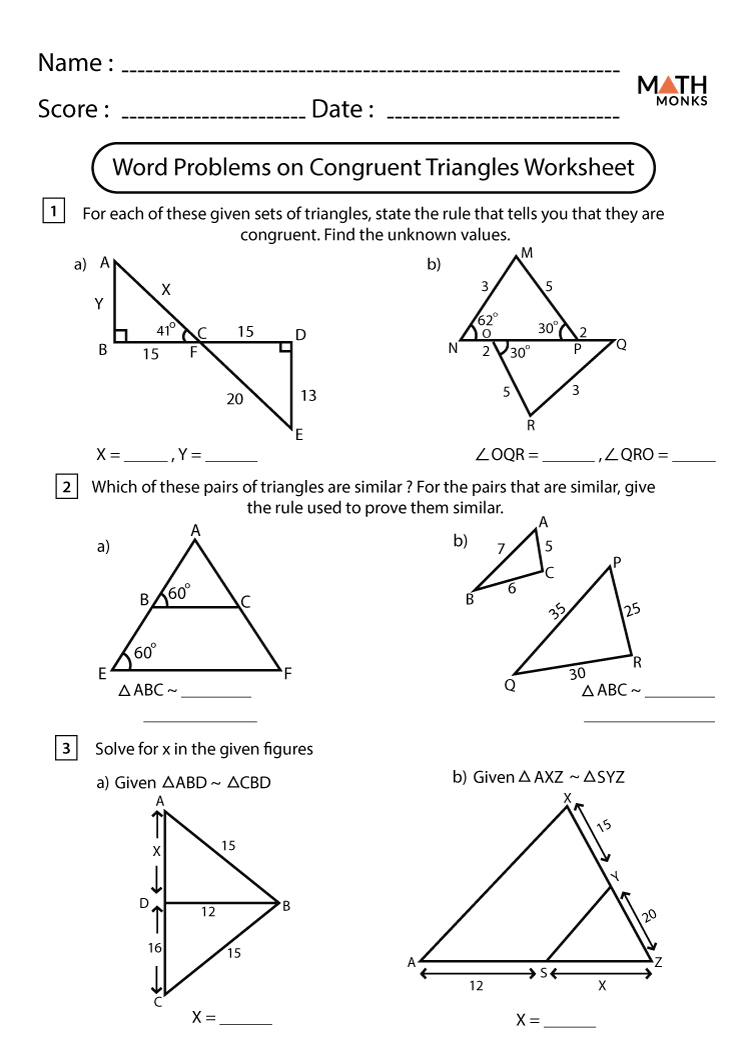
When students work with similar and congruent figures, several common mistakes can occur:
To avoid these pitfalls:
🔎 Note: Practice with visual aids or software can greatly help in understanding these concepts.
By incorporating similar and congruent figures into your mathematical toolkit, you enhance your ability to solve problems, create precise designs, and comprehend spatial relationships. These concepts not only help in tackling mathematical challenges but also in appreciating the underlying order of the world around us. Whether you're plotting out a garden, designing a building, or simply appreciating art and architecture, the principles of similarity and congruence come into play, demonstrating the fundamental beauty of geometry.
What is the difference between similarity and congruence?

+
Similarity means figures have the same shape but potentially different sizes, while congruence implies that figures are identical in both shape and size.
How do you prove two triangles are congruent?

+
Triangles can be proven congruent using various postulates like SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), AAS (Angle-Angle-Side), or HL (Hypotenuse-Leg for right triangles).
Can all polygons be similar?

+
No, all polygons are not necessarily similar. For polygons to be similar, all corresponding angles must be equal, and the ratios of all corresponding sides must be the same.