5 Essential Steps for Geometry Transformation Success

Understanding Geometry Transformations

Geometry is not just about shapes and figures; it’s also about understanding how these figures move and change. Transformation in geometry refers to the movement of objects in a plane without altering their shape. Understanding these transformations is fundamental for anyone involved in mathematics, design, engineering, or even computer graphics. Here are the 5 essential steps to ensure success in mastering geometry transformations.
Step 1: Grasp the Basics of Geometric Transformations

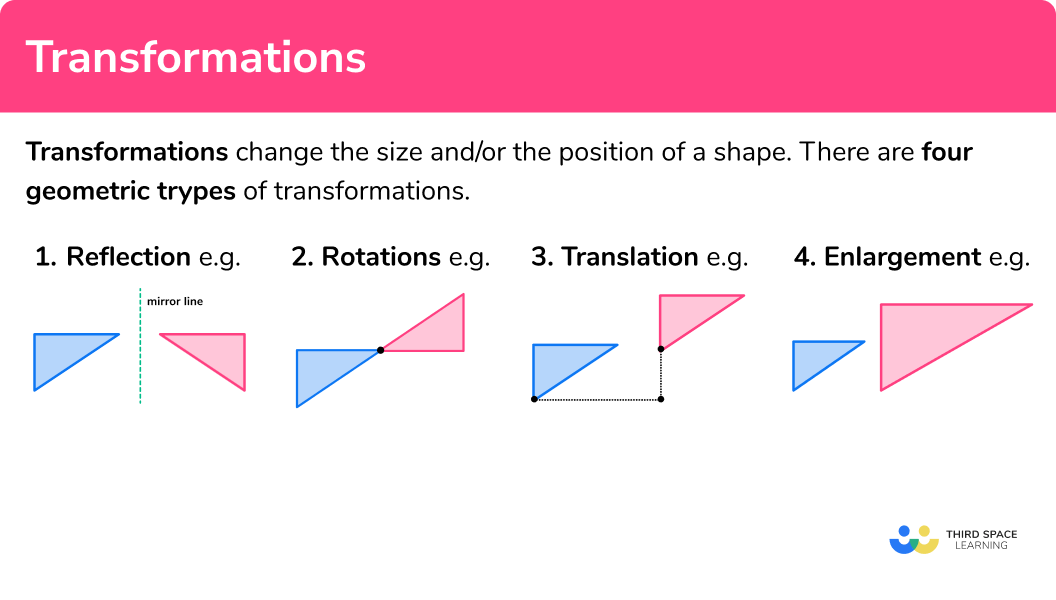
The foundation of geometric transformations lies in understanding the four basic types:
- Translation: Moving an object from one place to another without changing its size, shape, or orientation.
- Rotation: Turning an object around a fixed point, altering its orientation but not its shape or size.
- Reflection: Flipping an object over a line, which produces a mirror image.
- Dilation: Changing the size of an object while keeping its shape and proportion.
These transformations are often combined to create complex movements in real-world applications.
📚 Note: While these transformations can seem basic, their implications and applications in advanced mathematics and design are profound.
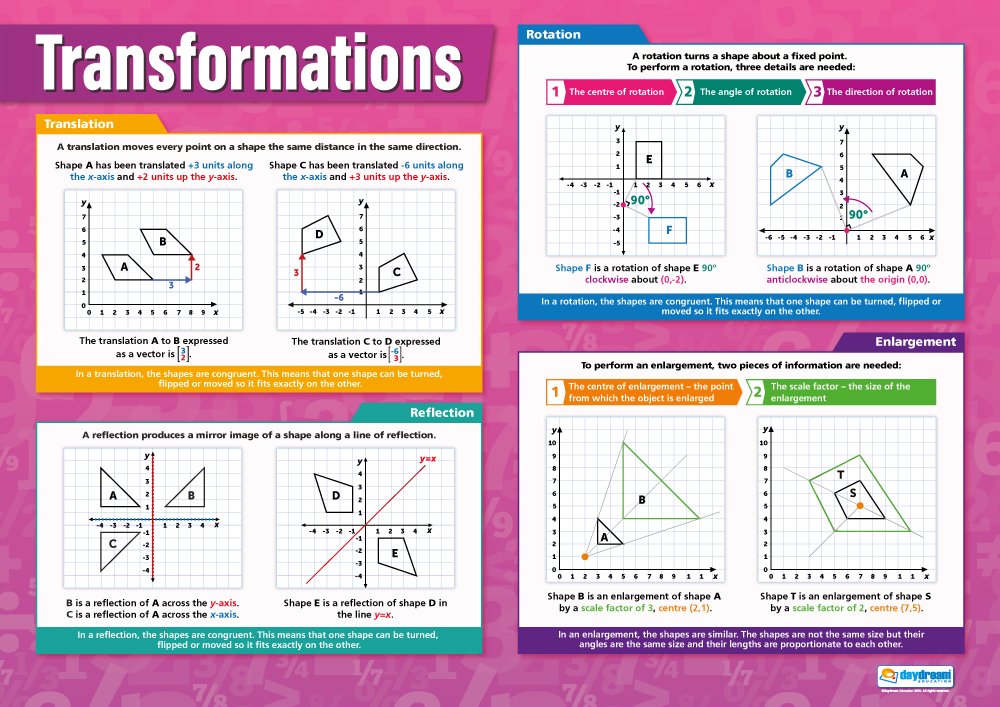
Step 2: Master the Formulas and Equations

Each transformation has its own set of formulas which are crucial for precision:
- For translation, know how to use coordinate changes.
- For rotation, memorize the rotation matrix or understand the rules for rotating points around a center.
- Reflections require understanding how to flip coordinates.
- Dilation involves scaling factors for each coordinate.
Here’s a table showing the basic transformation formulas:
| Transformation | Formula |
|---|---|
| Translation | (x’, y’) = (x + tx, y + ty) |
| Rotation | x’ = x cos(θ) - y sin(θ) y’ = x sin(θ) + y cos(θ) |
| Reflection over x-axis | (x’, y’) = (x, -y) |
| Dilation | (x’, y’) = (kx, ky) where k is the scale factor |

🔎 Note: Practicing these formulas with actual examples helps solidify the understanding of each transformation.
Step 3: Utilize Software and Tools
In today’s digital age, mastering geometric transformations is also about leveraging technology:
- Use software like GeoGebra, Desmos, or AutoCAD for visualizing transformations.
- These tools can simulate translations, rotations, and other transformations interactively, providing a dynamic learning experience.
Interactive simulations allow for instant feedback, making it easier to see the effects of transformations and understand the underlying principles.
Step 4: Apply Transformations in Real-World Contexts
Applying what you learn:
- Design and Art: Understand how artists manipulate images and patterns through geometric transformations.
- Engineering: Recognize transformations in mechanical systems or architectural design.
- Computer Graphics: Transformations are fundamental for animation, game development, and image manipulation.
By linking theory with application, you’ll deepen your understanding and find practical uses for what might otherwise seem abstract concepts.
Step 5: Continuous Learning and Problem Solving

Geometry transformations are not static; they evolve with problem complexity and new challenges:
- Engage with geometric puzzles, proofs, and higher-level mathematics that utilize transformations.
- Participate in workshops or online forums where real-world applications of geometry are discussed.
- Regularly practice through exercises or software challenges to keep your skills sharp.
The field of geometry is vast, and staying current with advancements can significantly boost your expertise.
Mastering geometry transformations is a rewarding journey that requires both theoretical knowledge and practical application. By understanding the basics, mastering the formulas, using technology wisely, applying concepts to real-world scenarios, and committing to continuous learning, you set yourself up for success not only in geometry but also in numerous fields where spatial understanding is essential. This holistic approach ensures that you are not just learning to transform shapes but are also enhancing your problem-solving skills, creativity, and technical proficiency.
What is the difference between a translation and a rotation?

+
A translation moves an object in a straight line without changing its orientation, while a rotation turns the object around a fixed point, altering its orientation but not its size or shape.
Why is technology important in learning geometry?

+
Technology like GeoGebra and AutoCAD provides visual and interactive simulations that can help learners visualize and understand abstract concepts like transformations in real-time.
How do transformations apply in art and design?
+
Artists and designers use transformations to manipulate shapes and patterns, creating symmetry, balance, and aesthetic appeal in their work.