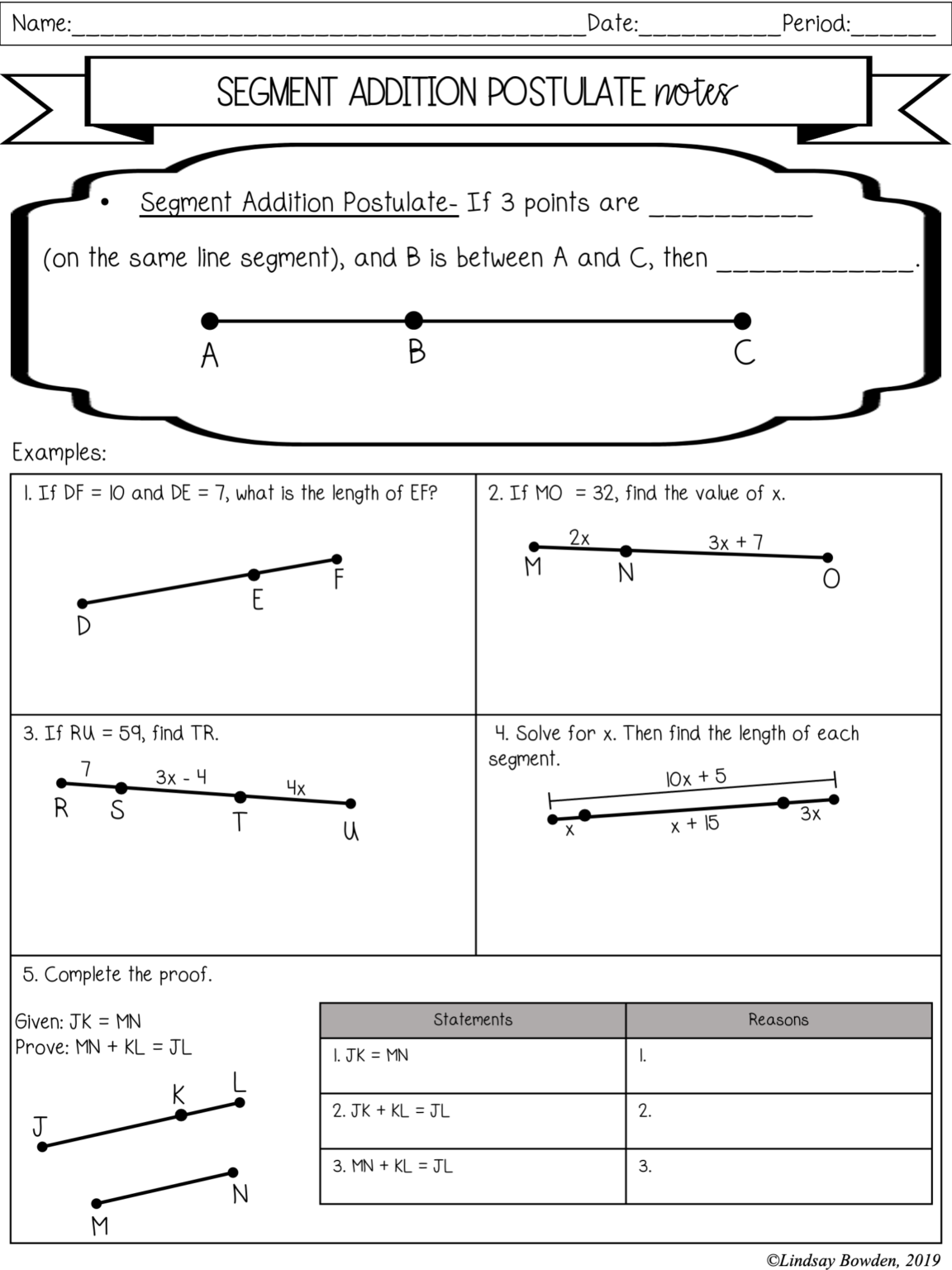
5 Tips for Mastering Segment Addition Postulate Worksheets

The Segment Addition Postulate is an essential concept in geometry that helps students understand how to work with line segments and their properties. Whether you're a student grappling with geometry or an educator striving to impart this knowledge, mastering the Segment Addition Postulate can significantly enhance your mathematical skills. Here are five tips to help you conquer those Segment Addition Postulate worksheets with confidence.
Understand the Concept Deeply

Before diving into the worksheets, it’s crucial to grasp the Segment Addition Postulate fundamentally. This postulate states that if three points A, B, and C are collinear, and B is between A and C, then AB + BC = AC. Here are some steps to internalize this:
- Visualize: Draw line segments on paper or use virtual geometry tools to understand how parts of a line add up to a whole.
- Practice with Simple Examples: Start with known lengths to calculate the total or find missing segments.
- Memorize the Formula: The formula AB + BC = AC becomes intuitive with practice.
💡 Note: Always check if the points are collinear to apply the Segment Addition Postulate correctly.
Mastering the Diagram

Segment Addition Postulate worksheets often include diagrams. Here’s how to make the most out of them:
- Label Clearly: Always label the points and lengths given. This can reduce confusion.
- Use Coloring: Color code segments to easily see which parts add up to form a whole segment.
- Verify Given Information: Make sure you understand the given information before solving.

Practice with Real-World Applications
Applying the Segment Addition Postulate to real-world scenarios can solidify understanding:
- Landmark Distances: Use maps or satellite images to find distances between cities or landmarks.
- Home Improvement: Calculate the length of wall segments for painting or decorating.
- Architecture: Understand how segments in a structure relate to each other.
📚 Note: Real-world examples can make the abstract concept of segment addition more relatable and easier to remember.
Develop Problem-Solving Strategies

Instead of solely relying on formulas, here are some strategies to help solve problems:
- Backward Reasoning: Start from the known to find the unknown. If you know the total length and one segment, subtract to find the other.
- Proportions: Sometimes, segments are proportional. Set up ratios to find missing lengths.
- Graphical Method: Plot points on a coordinate plane to visually solve problems.
🔍 Note: Segment Addition Postulate problems can often be approached from multiple angles, increasing your problem-solving skills.
Review and Reflect

After completing worksheets, take time to review:
- Correct Mistakes: Learn from errors to avoid repeating them.
- Understand Patterns: See if there are recurring problem types or strategies.
- Discuss with Peers or Mentors: Sharing and discussing solutions can offer new perspectives.
By employing these tips, not only will you master the Segment Addition Postulate worksheets, but you'll also enhance your overall problem-solving abilities in geometry. Remember that geometry, like any other math subject, is about practice and understanding concepts through various lenses.
As you continue your journey in geometry, keep in mind that patience and consistent practice are your allies. Each worksheet conquered brings you closer to a deeper understanding of space, distance, and mathematical logic, skills that will serve you well beyond the classroom.
Why is understanding the Segment Addition Postulate important in geometry?

+
Understanding the Segment Addition Postulate helps you to solve problems involving lengths of segments, visualize spatial relationships, and apply these concepts to real-world situations. It’s fundamental for understanding many geometric theorems and proofs.
Can I use the Segment Addition Postulate on any line segment?

+
Yes, provided that the points are collinear, meaning they lie on the same straight line. The postulate allows you to add or subtract segment lengths in a linear manner.
What should I do if I get a worksheet question wrong?

+
Review the problem to understand where you went wrong. Sometimes, it’s a simple calculation mistake; other times, you might have misunderstood the given information. Practice that specific type of problem more to build confidence.



