Scientific Notation: Mastering Operations in Seconds

What is Scientific Notation?

Scientific notation, also known as standard form or exponential notation, is a method used by scientists and mathematicians to express very large or very small numbers in a more manageable format. It consists of a number between 1 and 10, multiplied by 10 raised to a power, which reflects the scale of the number. For instance, instead of writing out the mass of Earth as 5,973,600,000,000,000,000,000,000 kilograms, it would be expressed as 5.9736 × 1024 kilograms.

How to Convert to Scientific Notation

To convert a regular number into scientific notation, follow these steps:
- Identify the decimal point: Where is the decimal point in your number?
- Move the decimal: Shift the decimal point so that there is only one non-zero digit to its left. This creates the coefficient part of the scientific notation.
- Count the moves: Note how many places you’ve moved the decimal. If you moved it to the right, the exponent will be negative; if to the left, it will be positive.
- Combine: The number is now written as the coefficient multiplied by 10 raised to the power of the number of decimal place moves.
🔬 Note: When converting numbers less than 1, the decimal point moves to the right, giving a negative exponent.
Operations with Scientific Notation

Mastering operations in scientific notation is crucial for scientists, engineers, and anyone dealing with extreme numerical values. Here’s how to approach different operations:
Addition and Subtraction

Before performing addition or subtraction, the exponents must be the same. Adjust the coefficients by moving the decimal to align exponents:
- If the exponents are already equal, simply add or subtract the coefficients.
- Adjust the numbers so their exponents are equal, then add or subtract the coefficients.
- The resulting exponent remains the same as the original numbers before adjustment.
Multiplication
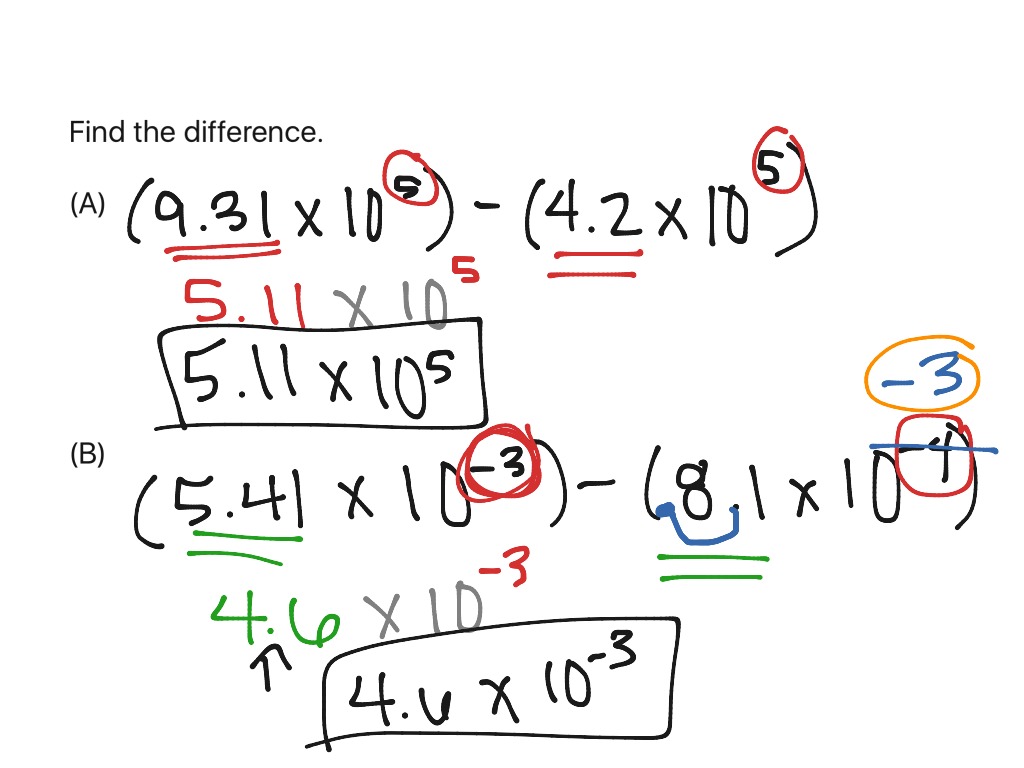
Multiplying numbers in scientific notation involves:
- Multiplying the coefficients together.
- Adding the exponents of the 10s.
- Ensuring the coefficient part of the result is between 1 and 10.
Division

For division in scientific notation:
- Divide the coefficient of the number in the numerator by the coefficient in the denominator.
- Subtract the exponent of the denominator from the exponent of the numerator.
- Convert the result back to scientific notation if necessary.
Examples of Operations

| Operation | Example | Process | Result |
|---|---|---|---|
| Addition | (3.2 × 10³) + (1.1 × 10³) | Convert 1.1 × 10³ to 11. × 10² (11 × 10²), then add coefficients: 3.2 + 1.1 = 4.3; Final: 4.3 × 10³ | 4.3 × 10³ |
| Multiplication | (4 × 10²) × (3 × 10⁴) | Multiply coefficients: 4 × 3 = 12; Add exponents: 10² + 10⁴ = 10⁶; Final: 12 × 10⁶ or 1.2 × 10⁷ | 1.2 × 10⁷ |
| Division | (6 × 10³) ÷ (2 × 10⁴) | Divide coefficients: 6 ÷ 2 = 3; Subtract exponents: 10³ - 10⁴ = 10-1; Final: 3 × 10-1 | 3 × 10-1 |

🔍 Note: When multiplying or dividing, adjustments to the coefficient might be needed to keep it within the standard scientific notation range of 1 to 10.
In summary, scientific notation offers a practical solution to handle unwieldy numerical data. By understanding how to convert to and operate with scientific notation, you unlock a powerful tool for simplifying arithmetic involving very large or very small numbers. While mastering operations in scientific notation might require some initial adjustment, the benefits in terms of speed and readability are undeniable. From scientists calculating the distance to the stars to engineers dealing with microelectronics, the utility of scientific notation is clear. As you practice these operations, remember to:
- Ensure exponent alignment in addition and subtraction
- Use coefficient manipulation wisely in multiplication and division
- Keep the coefficient between 1 and 10 for standardization
Why do we use scientific notation?

+
Scientific notation allows us to represent very large or very small numbers in a concise way, making calculations and comparison of such numbers much simpler.
Can you give an example of a real-world use of scientific notation?

+
In physics, the Planck length, the smallest length that has physical meaning, is often expressed as 1.616 × 10-35 meters, highlighting how scientific notation aids in understanding minute scales.
How do you convert scientific notation back to a standard number?

+
Move the decimal point in the coefficient to the right (for positive exponents) or left (for negative exponents) the number of places indicated by the exponent of 10.