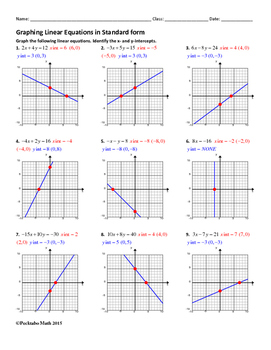
5 Key Solutions for Right Triangle Trig Worksheet

When students or educators encounter a right triangle trig worksheet, they often look for straightforward methods to solve the problems efficiently and accurately. Right triangle trigonometry, a fundamental part of algebra and geometry, revolves around understanding and calculating angles and sides of triangles. Here are five key solutions that can help anyone master these worksheets:
1. Understanding the Basic Trigonometric Functions

Mastering the basics of trigonometry is essential for tackling any trigonometry worksheet. The three primary trigonometric functions are:
- Sine (sin): Defined as opposite/hypotenuse
- Cosine (cos): Defined as adjacent/hypotenuse
- Tangent (tan): Defined as opposite/adjacent
Memorize these ratios, and practice them with various triangles to understand how they relate to one another.
🔍 Note: Remember SOH-CAH-TOA as an acronym for Sine, Cosine, and Tangent definitions.
2. Using Trigonometric Identities

Trigonometric identities help simplify problems. Key identities include:
| Identity | Description |
|---|---|
| sin²(θ) + cos²(θ) = 1 | The Pythagorean Identity |
| 1 + tan²(θ) = sec²(θ) | Relates tangent and secant |
| 1 + cot²(θ) = csc²(θ) | Relates cotangent and cosecant |

Applying these identities can help you solve equations or simplify expressions involving trigonometric functions.
3. Solving for Angles Using Inverse Functions
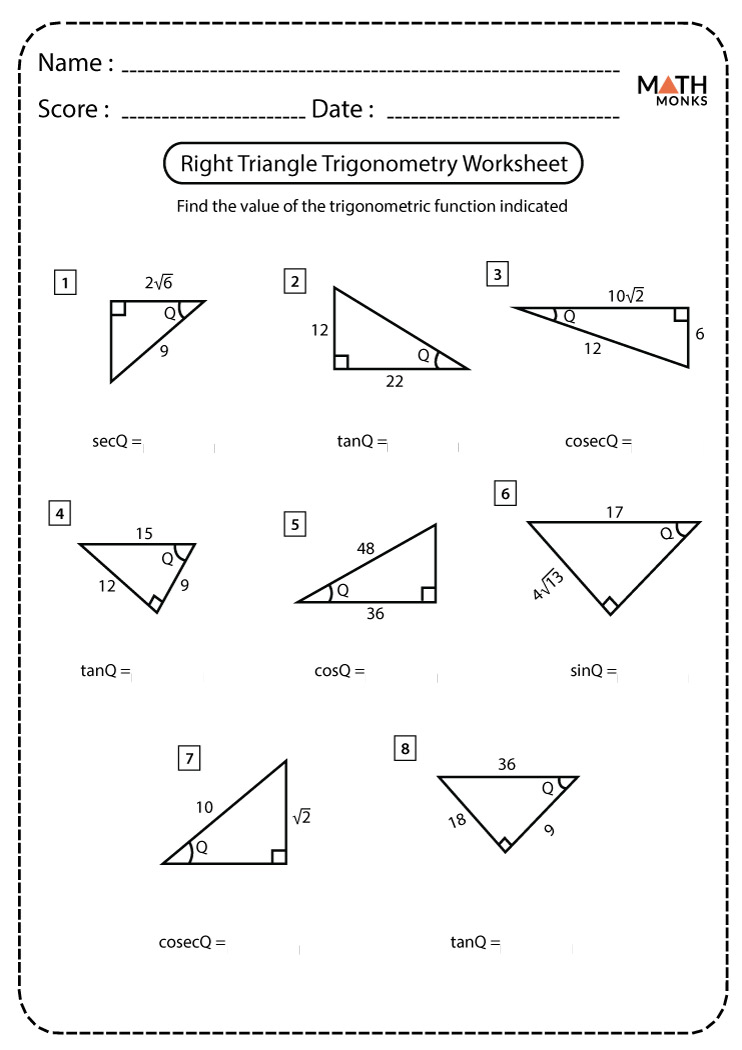
Not all worksheet problems involve finding sides; sometimes, you must determine an unknown angle. Use:
- sin⁻¹(x) or arcsin(x) for Sine Inverse
- cos⁻¹(x) or arccos(x) for Cosine Inverse
- tan⁻¹(x) or arctan(x) for Tangent Inverse
Understanding how to use these inverse functions correctly is crucial for solving trigonometric equations for angles.
4. Applying Pythagorean Theorem
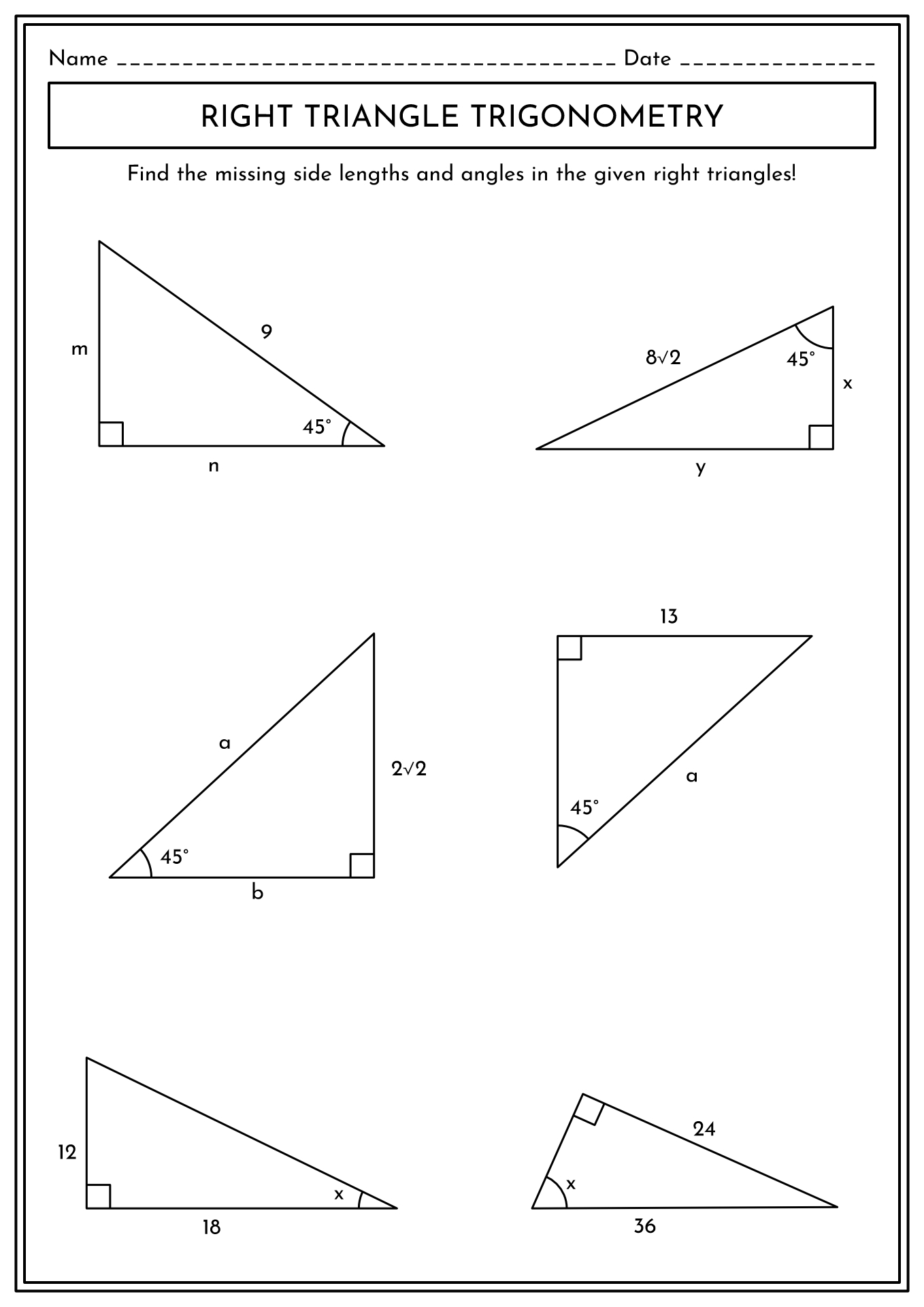
Often, worksheets include problems where the length of one side of a right triangle needs to be found using the relationship between the sides:
\[a^2 + b^2 = c^2\]
Here, 'a' and 'b' are the legs, and 'c' is the hypotenuse. Use this formula when you have two sides and need the third or when simplifying trigonometric expressions with the Pythagorean identity.
5. Systematic Approach to Word Problems

Trig word problems often involve translating everyday scenarios into a right triangle. Here’s a step-by-step approach:
- Identify the given information (angles, side lengths)
- Set up the triangle accordingly
- Decide which trigonometric function will help solve the problem
- Solve the problem using algebra or the Pythagorean theorem if needed
- Check your calculations to ensure accuracy
Example: A ladder leans against a wall, making a 30-degree angle with the ground. If the foot of the ladder is 4 feet from the wall, how high up the wall does the ladder reach?
You can solve this using:
- tan(30) = height/4 ft
- height = 4 ft × tan(30)
- height ≈ 4 ft × 0.577 = 2.31 ft
By applying these methods, one can systematically tackle the complexities found in a right triangle trig worksheet:
As we've gone through the strategies for mastering right triangle trigonometry, remember that practice is your ally. Here are some key takeaways to keep in mind:
- Master the three basic trigonometric functions and their properties.
- Learn and apply trigonometric identities to simplify and solve problems.
- Utilize inverse functions to find angles when needed.
- Combine Pythagorean theorem with trigonometric functions for a comprehensive understanding.
- Develop a systematic approach to word problems involving right triangles.
With these tools, you'll not only solve the problems on a worksheet but also enhance your overall understanding and appreciation of trigonometry. Keep practicing, and soon, these techniques will become second nature, making right triangle trigonometry not just a challenge, but a subject you can excel in.
Why do we use SOH-CAH-TOA?

+
SOH-CAH-TOA is a mnemonic that stands for Sin = Opposite/Hypotenuse, Cos = Adjacent/Hypotenuse, and Tan = Opposite/Adjacent. It’s used to remember the definitions of sine, cosine, and tangent in the context of a right triangle, making problem-solving more intuitive.
How can I tell which trigonometric function to use?
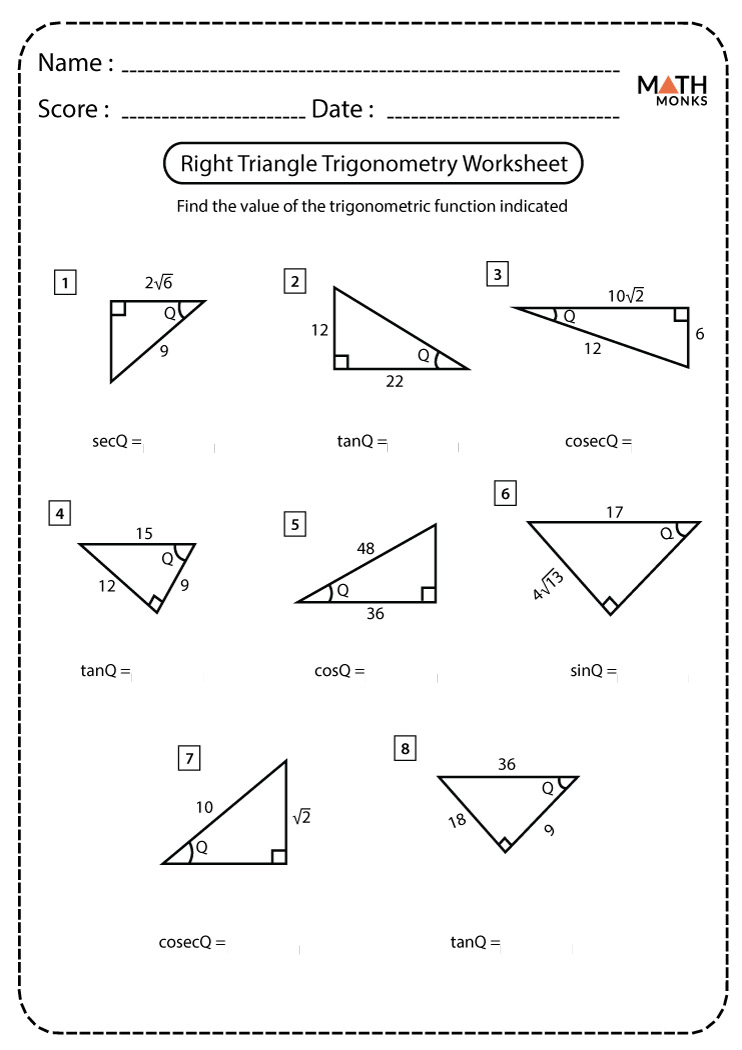
+
To decide which trigonometric function to use, identify which sides of the triangle are given and which you need to find. If you have the opposite and hypotenuse, use sine; if adjacent and hypotenuse, use cosine; if opposite and adjacent, use tangent.
Are there any common pitfalls in solving right triangle trig problems?
+
Common pitfalls include confusing the definitions of sine, cosine, and tangent, using the wrong identity, or not verifying which angle you are solving for or using the inverse function when not needed. Double-check your setup and use a calculator for accurate calculations.