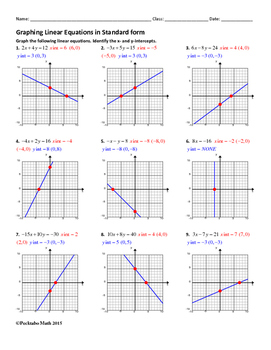
3 Easy Steps to Graph Linear Equations in Standard Form
Introduction to Graphing Linear Equations
Graphing linear equations might seem daunting for some learners, especially when they’re presented in standard form. However, with a clear understanding and a step-by-step approach, this task can become straightforward and even enjoyable. Linear equations in standard form are given as Ax + By = C, where A, B, and C are constants, and both x and y are variables.
Why Graph Linear Equations?

Graphing linear equations helps visualize relationships between variables, understand the behavior of linear functions, and solve problems in algebra, physics, and many other fields. By plotting these equations, you gain insights into:
- Slopes of lines and their steepness
- The intercepts, which tell you where the line crosses the x and y axes
- The solution set of a system of equations when plotted together
Step 1: Identify the X-Intercept

The first step in graphing a linear equation in standard form is finding the x-intercept. This is the point where the line crosses the x-axis, meaning the value of y at this point is 0.
To find the x-intercept:
- Set y equal to 0 in the standard form equation: Ax + By = C becomes Ax = C.
- Solve for x: x = C / A
📝 Note: If A equals 0, there is no x-intercept because the line is vertical.

Step 2: Identify the Y-Intercept
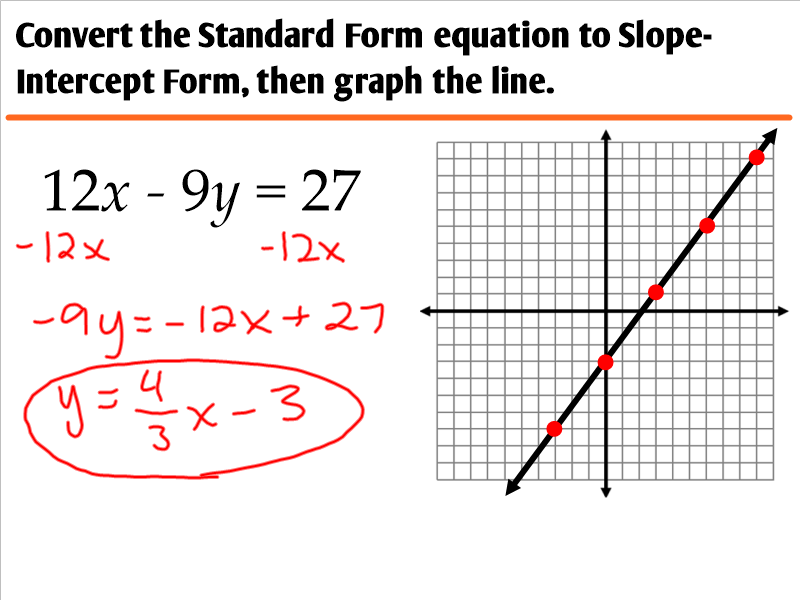
The y-intercept is where the line intersects the y-axis, meaning the value of x is 0 here.
To find the y-intercept:
- Set x equal to 0 in the equation: Ax + By = C turns into By = C.
- Solve for y: y = C / B
📝 Note: If B equals 0, there is no y-intercept because the line is horizontal.
Step 3: Plot and Draw the Line

With both intercepts identified, you can now:
- Plot the x-intercept on the x-axis and the y-intercept on the y-axis.
- Draw a straight line passing through these two points.
Here's a quick example:
| Equation | X-Intercept | Y-Intercept |
|---|---|---|
| 2x + 3y = 6 | (3, 0) | (0, 2) |
| -x + y = 3 | (-3, 0) | (0, 3) |

Using the intercepts from the table:
- For the equation 2x + 3y = 6, plot (3, 0) and (0, 2) then connect them.
- For -x + y = 3, plot (-3, 0) and (0, 3) and draw the line.
Additional Tips for Graphing

- Use graph paper for precision.
- Label the axes and points for clarity.
- Understand the slope-intercept form (y = mx + b) to double-check your graph.
Summing up, graphing linear equations in standard form involves three easy steps: identifying x and y intercepts, plotting them, and drawing the line. This method not only helps in visualizing the equation but also in solving and understanding linear systems and their properties.
What if the coefficients A or B are negative?

+
Negative coefficients do not affect the method of finding intercepts; they only change the direction or position of the line. If A is negative, the x-intercept will be positive, and if B is negative, the y-intercept will be positive.
Can I use the intercept method if the equation is not in standard form?

+
The method works best for equations in standard form. For other forms like slope-intercept or point-slope, you might need to convert them into standard form first.
What if there’s no intercept?

+
If either the x or y coefficient (A or B) is zero, the line will be vertical or horizontal, respectively. In such cases, you might only have one intercept, or in some cases, none if the line passes through the origin or has no intercept.
Can you plot a linear equation with just one point?

+
With just one point, you can plot that point but can’t draw a unique line since infinitely many lines can pass through a single point. At least two distinct points are required to determine a unique line.
How do slopes relate to the standard form?

+
The slope of a line in standard form can be found using the formula m = -A / B, where A and B are the coefficients from the standard form Ax + By = C.