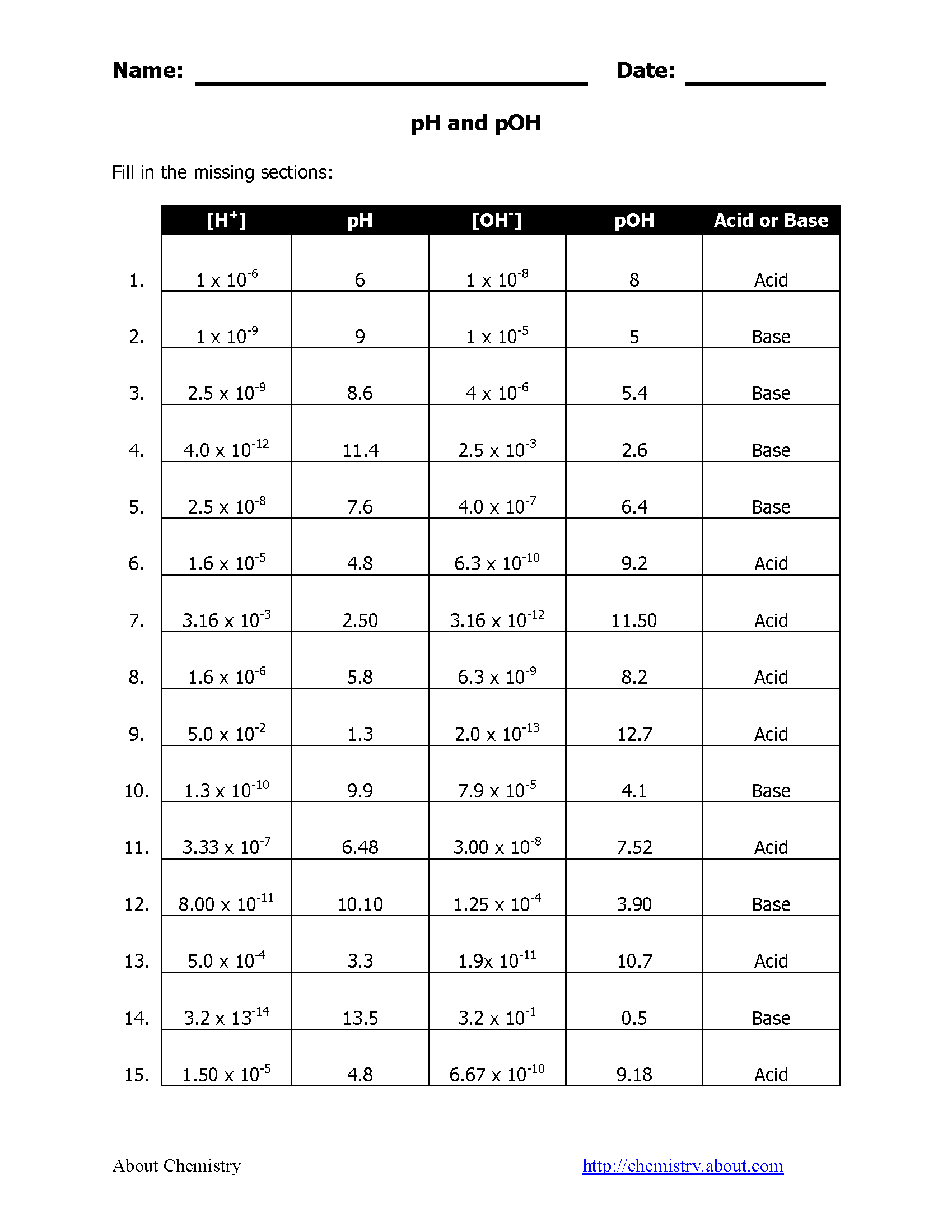
Convert Repeating Decimals to Fractions Easily: Free Worksheet

Understanding Repeating Decimals

Before diving into the conversion of repeating decimals into fractions, it’s essential to grasp what a repeating decimal is. A repeating decimal, or a recurring decimal, is a decimal that has a digit or a sequence of digits that repeats indefinitely. For example, (0.3333\ldots) or (0.142857142857\ldots) are repeating decimals, where (3) and (142857) are the repeating sequences respectively.
Why Convert Repeating Decimals to Fractions?

Converting repeating decimals to fractions is beneficial for several reasons:
- Simplicity: Fractions can be easier to work with, especially when performing calculations or solving algebraic equations.
- Exactness: Unlike repeating decimals, fractions represent exact values without an infinite string of digits.
- Understanding: Sometimes understanding a number’s magnitude is clearer with fractions, especially in contexts like probability or rate calculations.
How to Convert Repeating Decimals to Fractions

Here’s a step-by-step guide on how to convert any repeating decimal into a fraction:
Step 1: Define the Variables
Let ( x ) be the repeating decimal you want to convert. For example, if you want to convert (0.\overline{3}) into a fraction, let ( x = 0.3333\ldots ).
Step 2: Set up the Equations

To eliminate the repeating part, multiply ( x ) by a power of 10 that will shift the repeating decimal place to the right. If the repeating sequence is one digit long, multiply by 10; if it’s two digits, multiply by 100, and so on. For (0.\overline{3}), multiply by 10 to get:
[ 10x = 3.333\ldots ]Step 3: Create and Subtract the Equations

Now, subtract the original equation from this new equation:
[ 10x - x = 3.333\ldots - 0.333\ldots ] [ 9x = 3 ] [ x = \frac{3}{9} ]Step 4: Simplify the Fraction

Reduce the fraction to its lowest terms:
[ x = \frac{1}{3} ]Step 5: Handle Complex Repeating Sequences

For decimals with longer repeating sequences or non-repeating parts, the process remains similar but involves more steps:
- If the decimal is (0.\overline{12}), multiply ( x ) by 100 to get ( 100x = 12.1212\ldots ), then subtract ( x = 0.1212\ldots ).
- If the decimal has a non-repeating part, like (0.45\overline{36}), create two equations: one by multiplying ( x ) by 100 to shift the decimal, and another by multiplying ( x ) by a power of 10 that aligns with the end of the non-repeating part, then subtract them.
✏️ Note: When dealing with repeating decimals that have both repeating and non-repeating parts, be extra careful in aligning the decimal places before subtraction.
Worksheet for Practicing Conversion

To solidify your understanding of converting repeating decimals to fractions, here’s a free worksheet:
| Repeating Decimal | Fraction Equivalent |
|---|---|
| 0.\overline{3} | |
| 0.1\overline{8} | |
| 0.3\overline{6} | |
| 0.0\overline{12} |

Fill in the table above, applying the steps learned in this blog. This practice will help you master the conversion process.
In summary, converting repeating decimals to fractions is a method that simplifies mathematical operations, provides exact values, and enhances the comprehension of numbers. The process involves setting up equations, eliminating the repeating part, and simplifying the resulting fraction. With practice, this conversion will become second nature, making your math work more straightforward and insightful.
What is a repeating decimal?

+
A repeating decimal is a decimal representation of a number where a digit or sequence of digits repeats indefinitely.
Why should I convert repeating decimals to fractions?

+
Converting repeating decimals to fractions can simplify arithmetic operations, provide exact values, and make understanding quantities easier.
Can all decimals be converted to fractions?

+
Yes, all repeating or terminating decimals can be expressed as fractions, as they represent rational numbers.
What if there is a non-repeating part before the repeating part?

+
You can still convert it by setting up two equations—one aligning with the non-repeating part and another shifting the decimal to capture the repeating part, then subtract them.
How do I simplify the resulting fraction?
+To simplify, divide both the numerator and the denominator by their greatest common divisor (GCD).