Unlocking Nuclear Secrets: Radioactivity Worksheet Answers Explained

Welcome to our comprehensive guide on understanding and solving radioactivity worksheet problems. This subject matter is not only vital for students aiming to grasp complex physics concepts but also for anyone interested in the applications of nuclear science, from medical treatments to energy production. In this blog post, we'll explore the foundational concepts of radioactivity, explain common problems encountered in worksheets, and provide detailed answers to help you navigate through this intricate topic with ease.
Understanding Radioactivity

Radioactivity is the process by which unstable atomic nuclei emit particles or energy to achieve stability. Here’s a quick overview:
- Alpha Decay: An alpha particle (two protons and two neutrons, essentially a helium nucleus) is emitted.
- Beta Decay: A beta particle (an electron or positron) is released, often accompanied by an antineutrino or neutrino.
- Gamma Decay: High-energy gamma rays are emitted, usually following alpha or beta decay to remove excess energy from the nucleus.
/alpha_beta_gamma_rays-579fb5d65f9b585815609b54.jpg)
⚛️ Note: Make sure you understand how different types of decay affect the atomic number and mass number of an atom.
Decoding Radioactive Decay

When tackling a worksheet on radioactivity, here are key steps:
- Identify the Decay Type: Determine if it’s an alpha, beta, or gamma emission based on the change in the atomic and mass numbers.
- Balancing Equations: Ensure that the mass number and atomic number on both sides of the decay equation balance out.
- Half-Life Calculations: Use the equation ( N = N0 \left(\frac{1}{2}\right)^{\frac{t}{T{1⁄2}}} ), where:
- (N) is the remaining quantity of the substance
- (N0) is the initial quantity
- (t) is the elapsed time
- (T{1⁄2}) is the half-life of the substance.
Examples and Worksheet Answers

Let’s walk through some common questions found in radioactivity worksheets:
Example 1: Balancing Alpha Decay

Given the equation:
[ ^{226}{88}Ra \rightarrow ^{222}{86}Rn + \alpha ]
We can see that:
- The atomic number (number of protons) decreases by 2, and the mass number decreases by 4.
- This confirms that it’s an alpha decay, as alpha particles consist of 2 protons and 2 neutrons.
🔍 Note: Always double-check your mass and atomic numbers to ensure conservation of both in your decay equations.
Example 2: Beta Decay

Consider the following:
[ ^{32}{15}P \rightarrow ^{32}{16}S + \beta^- ]
- Here, the mass number remains the same, but the atomic number increases by 1 due to a neutron turning into a proton.
- The emitted particle is an electron (\beta^-), accompanied by an antineutrino.
Example 3: Half-Life Calculations

If you have 4 grams of cobalt-60 with a half-life of 5.27 years, how much will remain after 15.81 years?
Using the formula:
[ N = 4 \left(\frac{1}{2}\right)^{\frac{15.81}{5.27}} \approx 0.5 \text{ grams} ]
🕐 Note: The half-life concept simplifies many calculations but remember, after each half-life period, only half of the previous amount remains.
Applications of Radioactivity

Understanding radioactivity isn’t just academic; here are some practical applications:
| Application | Explanation |
|---|---|
| Medical Treatments | Radiation therapy uses gamma or beta rays to kill cancer cells. |
| Energy Production | Nuclear reactors leverage nuclear fission to produce heat and subsequently electricity. |
| Carbon Dating | Carbon-14 dating helps to determine the age of organic material based on decay rates. |
| Security Screening | Gamma radiation can detect explosives or weapons through luggage scanning. |
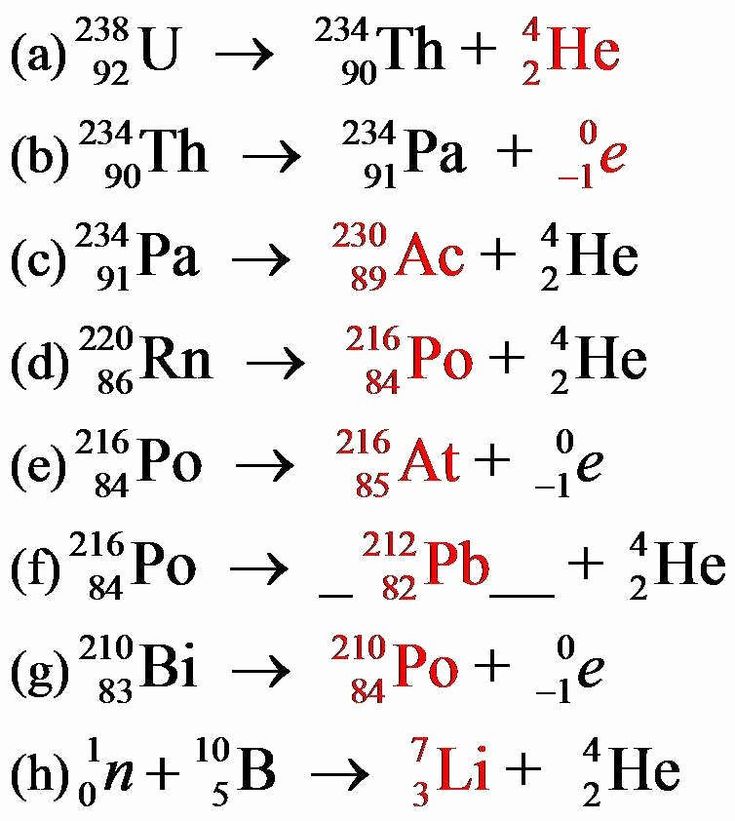
In our journey through radioactivity, we've covered foundational concepts, solved typical worksheet problems, and explored real-world applications. Understanding how radioactive decay works, the types of radiation, and the implications of half-life calculations can open doors to numerous fields of science, from medical diagnostics to sustainable energy solutions. Always keep in mind the safety measures around radioactive materials, and consider the profound effects that nuclear science has on our environment and technology.
What is meant by alpha decay?

+
Alpha decay is a type of radioactive decay where an alpha particle (two protons and two neutrons) is emitted from the nucleus of an atom, reducing its mass number by 4 and atomic number by 2.
How do you calculate the half-life of a radioactive substance?

+
The half-life of a radioactive substance is calculated using the formula: ( T_{1⁄2} = \frac{0.693}{\lambda} ), where ( \lambda ) is the decay constant. For any substance, you can also calculate remaining amounts after a given time with the equation: ( N = N0 \left(\frac{1}{2}\right)^{\frac{t}{T{1⁄2}}} ).
Can radioactivity be used for everyday applications?

+
Yes, absolutely. From carbon dating archaeological remains, to cancer treatment, to generating electricity, radioactivity plays a crucial role in both research and practical applications, making it an integral part of our daily lives.
Why is understanding radioactivity important for students?

+
Understanding radioactivity equips students with knowledge that has applications in physics, chemistry, medicine, and environmental science. It also fosters critical thinking in handling complex scientific problems and has implications for future technologies and safety protocols.



