Mastering Trig: 5 Law of Sines and Cosines Hacks

In the quest to conquer trigonometry, many students encounter hurdles when it comes to solving complex triangle problems. The Law of Sines and Cosines are essential tools in this journey, providing a structured method to work through triangles when traditional methods like the Pythagorean Theorem are insufficient. Here are five hacks to help you master these laws and elevate your trigonometry skills.
The First Hack: Understanding the Foundations

Before diving into hacks, it’s critical to understand what these laws entail:
- Law of Sines: States that in any triangle, the ratio of the length of a side to the sine of the opposite angle is constant for all three sides. The formula is:
a / sin(A) = b / sin(B) = c / sin©
- Law of Cosines: Useful for finding any unknown side or angle when you have at least three pieces of information. The formula is:
c2 = a2 + b2 - 2ab cos©
🎯 Note: Always draw and label a diagram of your triangle when applying these laws. This visual representation helps in reducing calculation errors.
The Second Hack: Using Technology Effectively

Technology can be a powerful ally:
- Use graphing calculators or apps like Desmos to graph triangles and visualize angles and sides. This visualization helps in understanding the problem’s complexity.
- There are many online calculators specifically designed for trigonometric calculations, which can be lifesavers when checking your work or solving complex problems.
The Third Hack: Smart Calculation Strategies

Simplify your work with these strategies:
- Round Off Early: After ensuring you have the correct values, round off numbers early in your calculations to avoid dealing with long decimal sequences.
- Estimate: Sometimes, a quick estimation can provide a sanity check before you dive into detailed calculations.
- Practice with Known Values: Solve triangles where you know the results to understand how errors can occur and how to correct them.
| Example | Given | Calculate |
|---|---|---|
| Example 1 | a = 10, B = 30°, b = 8 | Use Law of Cosines for C |
| Example 2 | a = 7, b = 5, c = 6 | Use Law of Cosines to find one angle, then use Law of Sines for others |
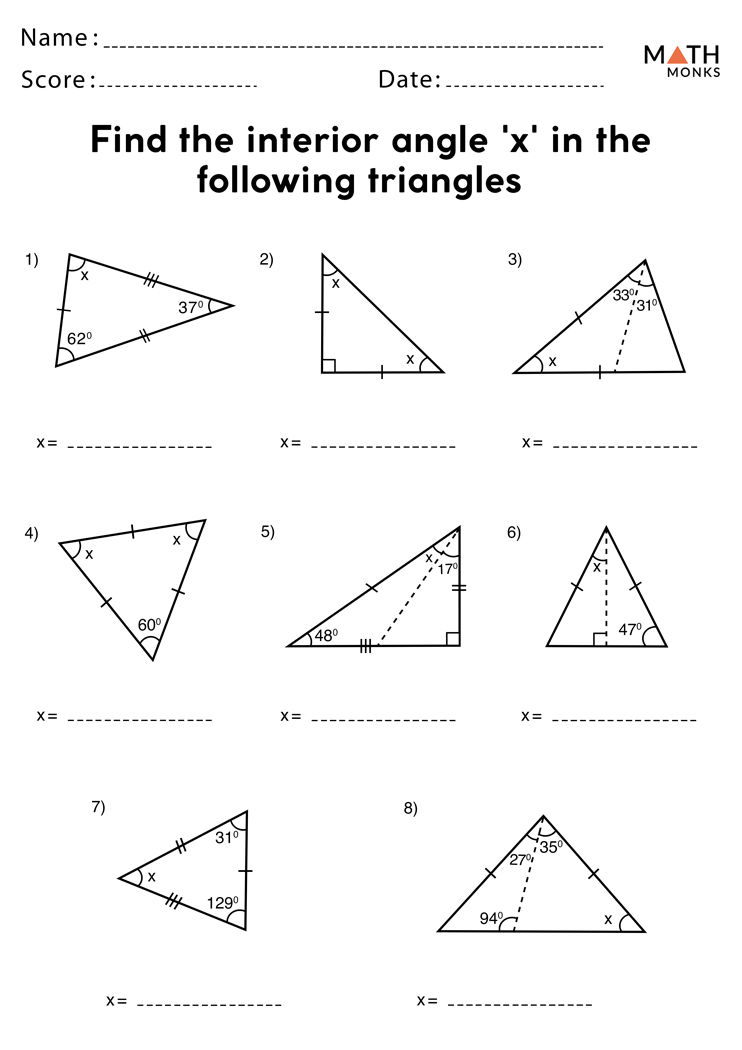
The Fourth Hack: The Ambiguous Case

The Law of Sines can sometimes yield two different triangles for the same set of data:
- When given two sides and a non-included angle (SSA), you can face the Ambiguous Case where:
- The angle might not produce a triangle
- It could produce one triangle
- Or it could produce two distinct triangles
- Hack: Determine the height of the triangle using the sine of the given angle and the length of the shorter side. If this height is less than or equal to the other given side, you might have two triangles.
🏹 Note: Always remember, when dealing with SSA, check for the ambiguous case. This isn't an error; it's a feature of trigonometry!
The Fifth Hack: Combine Methods

When solving complex problems, combine the Law of Sines and Cosines:
- Use Law of Cosines first: If you have sides, find an angle. If you have angles, find a side. This can often make the problem more tractable.
- Then employ Law of Sines: For the remaining sides or angles, this law can simplify calculations since you now have a known angle to work with.
With these hacks in your toolkit, mastering the Law of Sines and Cosines becomes less of a daunting task. Remember, practice is your best ally in trigonometry. The more you apply these laws, the more intuitive they become. Also, keep an eye on your units and decimal places to ensure accuracy in your calculations.
What is the Ambiguous Case in the Law of Sines?

+
The Ambiguous Case refers to the situation in triangle trigonometry where two sides and an angle opposite one of these sides (SSA) could potentially result in two different triangles, one triangle, or no triangle at all.
How can I remember the difference between Law of Sines and Cosines?

+
Think of “Sine” (S) for angles and sides and “Cosine” © for all sides and the angle between them. Law of Sines deals with ratios of sides to the sine of their opposite angles, while the Law of Cosines involves all sides of the triangle along with the cosine of one angle.
Can I use Law of Sines or Cosines with right triangles?

+
Yes, but the Law of Cosines is particularly useful when dealing with non-right angled triangles or when you need to find an angle or side in a right triangle where you have two sides and an angle other than 90 degrees.