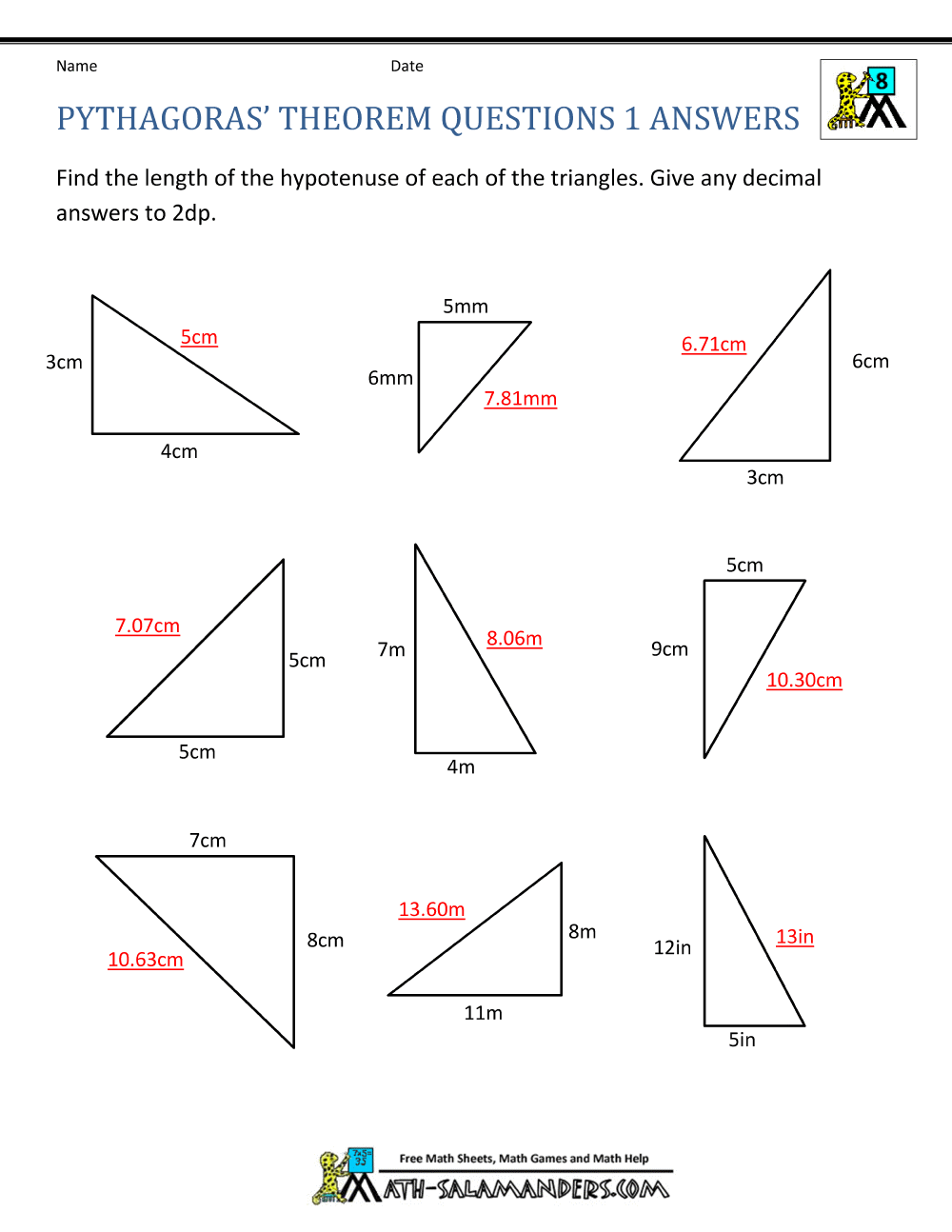
Pythagorean Theorem Worksheet Answer Key Geometry Revealed
One of the most fundamental principles in geometry is the Pythagorean Theorem, named after the ancient Greek mathematician Pythagoras. This theorem is not only a cornerstone in the study of geometry but also serves as a practical tool in various real-life applications. In this post, we will delve deep into the Pythagorean Theorem, explore its significance, and provide a worksheet with answer keys to help students and enthusiasts understand and apply it effectively.
Understanding the Pythagorean Theorem

The Pythagorean Theorem states that:
- In a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
- This relationship can be mathematically expressed as:
- a² + b² = c², where c is the hypotenuse, and a and b are the legs of the triangle.
To visualize this, consider a triangle with sides of length 3 and 4. If you square these (9 and 16), and add them together, you get 25. The square root of 25 is 5, which must be the length of the hypotenuse. Here's how it works:
| Side 'a' | Side 'b' | Side 'c' (Hypotenuse) | Verification |
|---|---|---|---|
| 3 | 4 | 5 | 3² + 4² = 5² or 9 + 16 = 25 |

📚 Note: Remember that this theorem only applies to right-angled triangles!
Practical Applications

Why is the Pythagorean Theorem important? Here are some practical applications:
- Construction and Architecture: To ensure structures are square or to calculate diagonal measurements.
- Navigation: Used in sea and air navigation for calculating distances.
- Computer Graphics: For algorithms involving 3D space and projection.
- Art and Design: Creating symmetrical patterns and perspective drawings.
Worksheet: Practicing the Pythagorean Theorem

Below is a worksheet designed to test and enhance your understanding of the Pythagorean Theorem:
Problem Set

Find the missing side of each right triangle:
- 1. a = 6, b = 8, c = ?
- 2. a = 9, c = 15, b = ?
- 3. b = 12, c = 13, a = ?
Answer Key

Answers:
- 1. c = √(6² + 8²) = √(36 + 64) = √100 = 10
- 2. b = √(15² - 9²) = √(225 - 81) = √144 = 12
- 3. a = √(13² - 12²) = √(169 - 144) = √25 = 5
Using these examples, you can see how the theorem is applied to find unknown sides in right triangles.
🔧 Note: The square root of a number can be approximated using a calculator or calculated manually using methods like long division.
Expanding the Theorem

The Pythagorean Theorem can be generalized into more complex geometric shapes and spaces:
- Generalized Pythagorean Theorem: For any triangle, not just right-angled, there's a similar theorem involving the incenter, circumcenter, and orthocenter.
- Pythagorean Triples: Sets of three positive integers (a, b, c) that satisfy a² + b² = c², like (3, 4, 5) or (5, 12, 13).
Wrapping Up

In summary, the Pythagorean Theorem offers a simple yet profound insight into the properties of right triangles. It's a testament to how elegant solutions can be found even in the complexity of geometry. Through this post, we've covered the fundamentals of the theorem, provided practical applications, and included a worksheet with solutions to help reinforce learning. Whether you're a student, a professional, or simply someone with a curiosity for mathematical beauty, the Pythagorean Theorem stands as a timeless example of how ancient wisdom continues to influence modern applications. This theorem not only enhances our problem-solving skills but also connects us to centuries of mathematical exploration and discovery.
What are Pythagorean triples?

+
Pythagorean triples are sets of three positive integers (a, b, c) such that a² + b² = c². Common examples include (3, 4, 5), (5, 12, 13), and (7, 24, 25).
Does the Pythagorean Theorem work for non-right angled triangles?

+
While the Pythagorean Theorem strictly applies to right-angled triangles, there are generalized versions for other types of triangles involving incenter, circumcenter, and orthocenter relationships.
How is the Pythagorean Theorem used in real-life scenarios?

+
The theorem is used in navigation to calculate distances, in construction to ensure right angles, in computer graphics for rendering, and even in art for creating balanced compositions.
What if one side is negative?

+
Side lengths of a triangle are inherently positive; negative sides do not represent physical lengths in Euclidean geometry.
Can the Pythagorean Theorem be used to verify if a triangle is a right triangle?

+
Yes, if you know the three sides of any triangle, you can use the theorem in reverse. If the sum of the squares of the two shorter sides equals the square of the longest side, then the triangle is a right triangle.