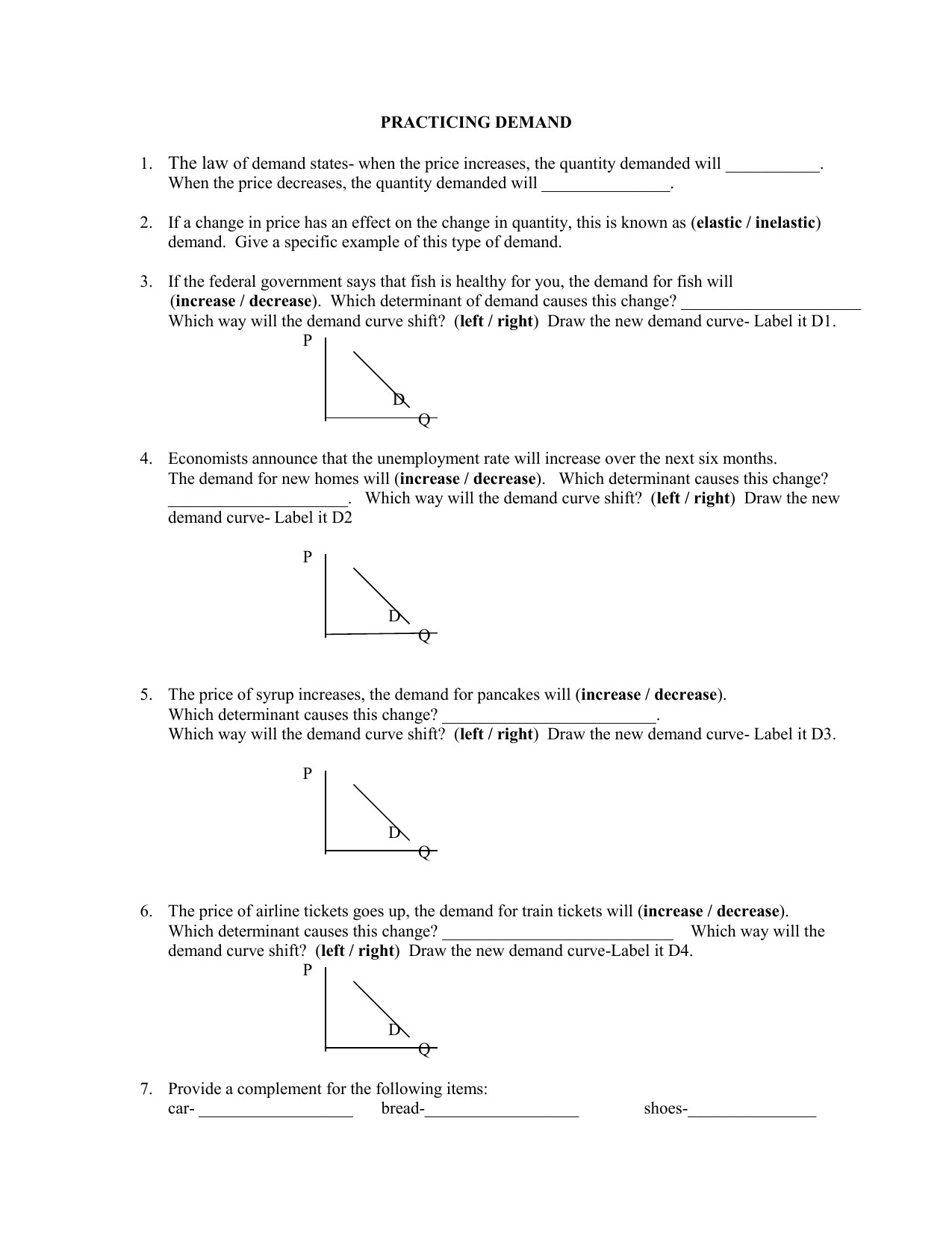
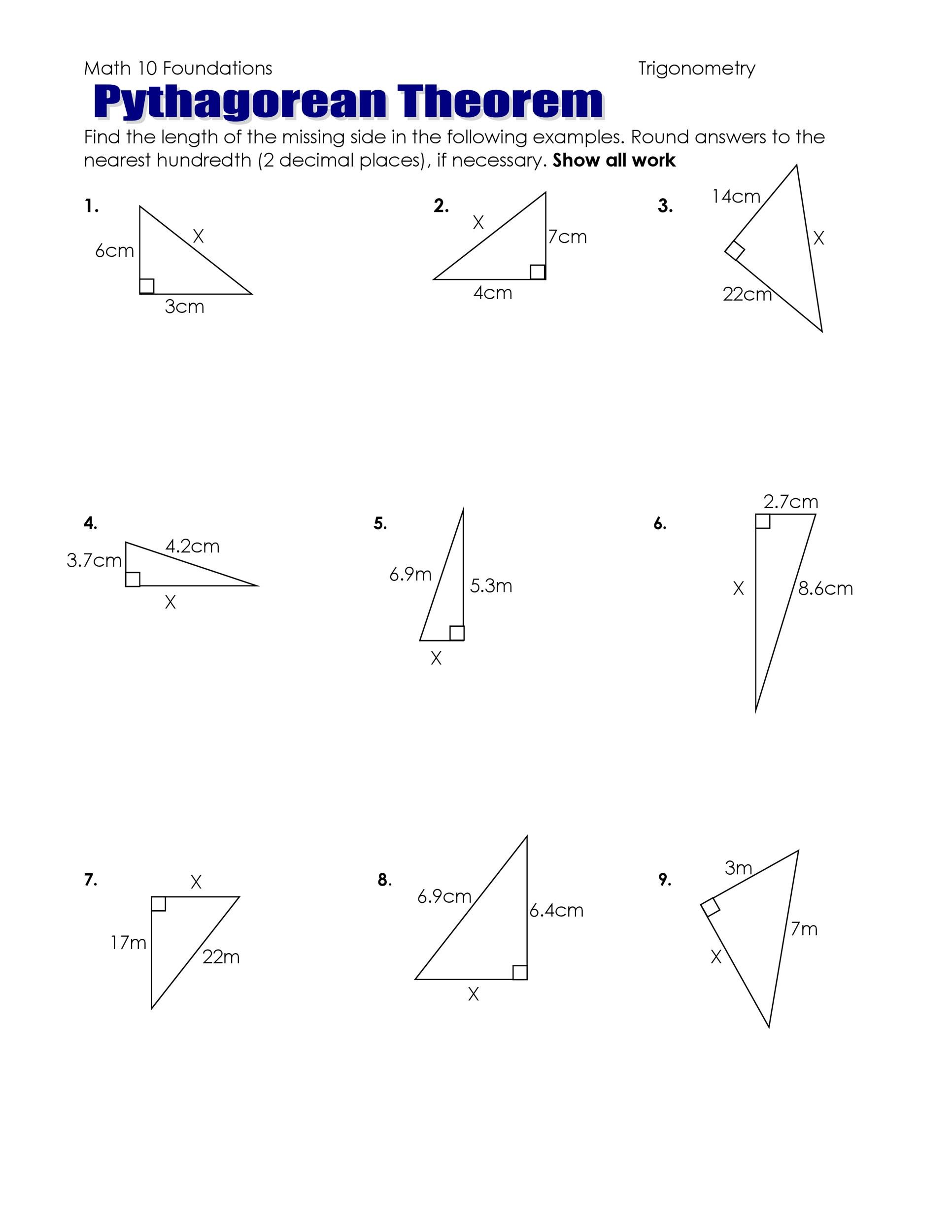
Pythagorean Theorem Worksheet Answer Key: 5 Quick Checks
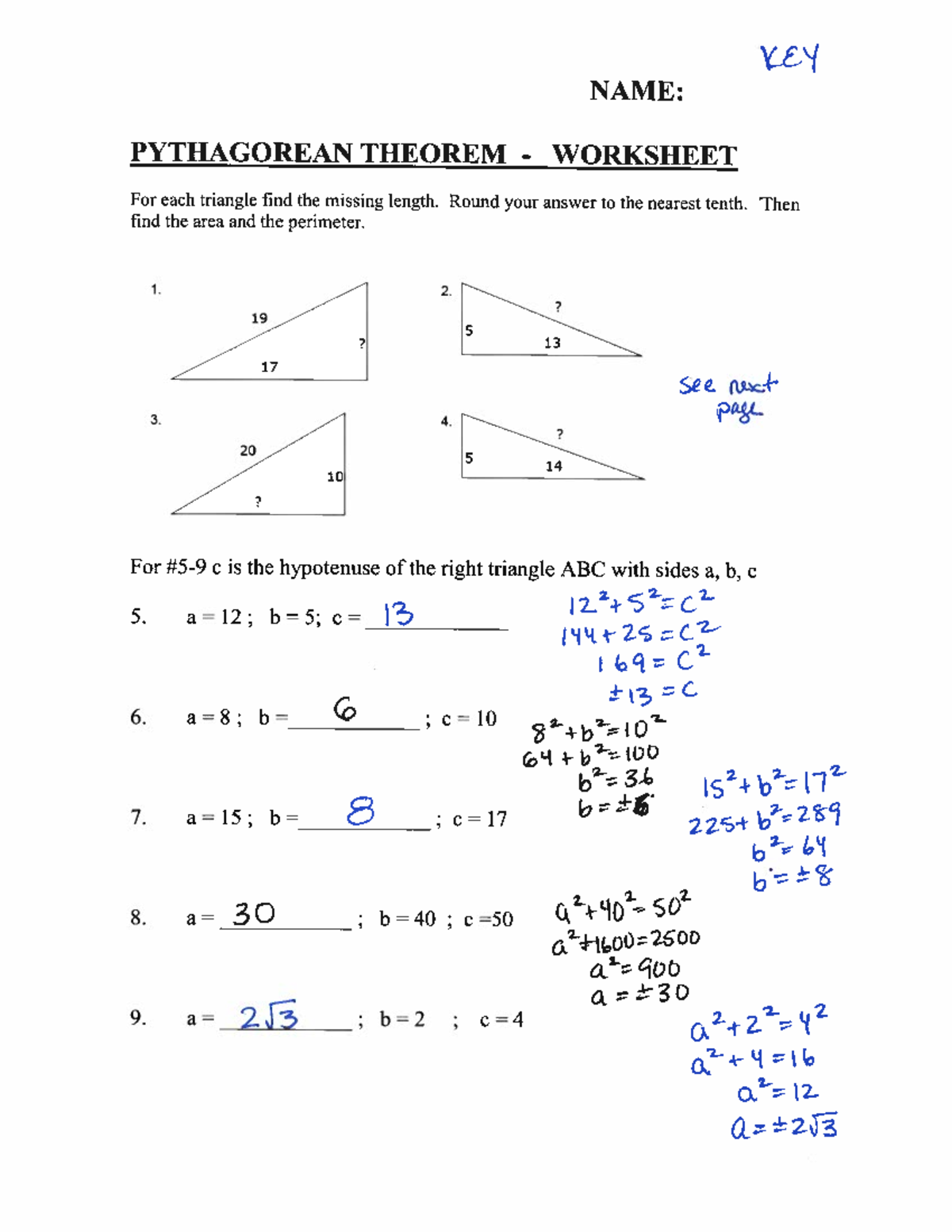
Understanding the Pythagorean theorem can be quite a game-changer in the world of geometry and beyond. It's a fundamental principle not just for finding the length of sides in right triangles, but also a cornerstone for various real-world applications. If you're working through a Pythagorean theorem worksheet and need some quick checks to ensure your answers are on the right track, this article is for you. Here, we'll provide an answer key for 5 selected problems along with some insights to help deepen your understanding of this theorem.
Preliminary Knowledge: The Pythagorean Theorem
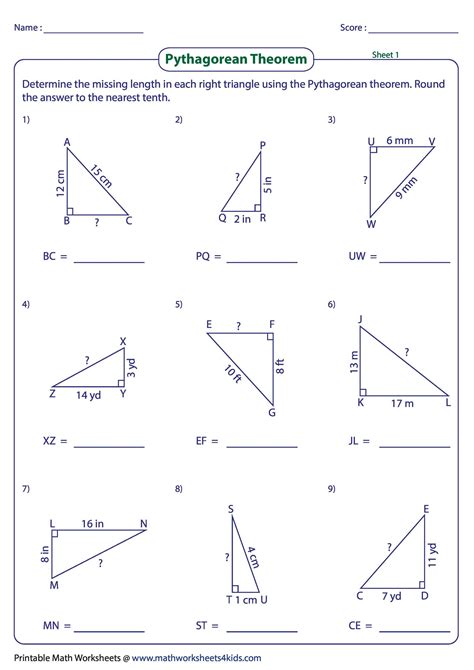
Before diving into our answer key, let's refresh on what the Pythagorean theorem actually states:
a² + b² = c²
Where:
- a and b are the legs of the right triangle.
- c is the hypotenuse, the longest side opposite the right angle.
Quick Checks: Answer Key for 5 Pythagorean Theorem Problems

Problem 1

Given the legs are 3 and 4 units, find the length of the hypotenuse c.
Using the Pythagorean theorem:
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25 = 5
Problem 2
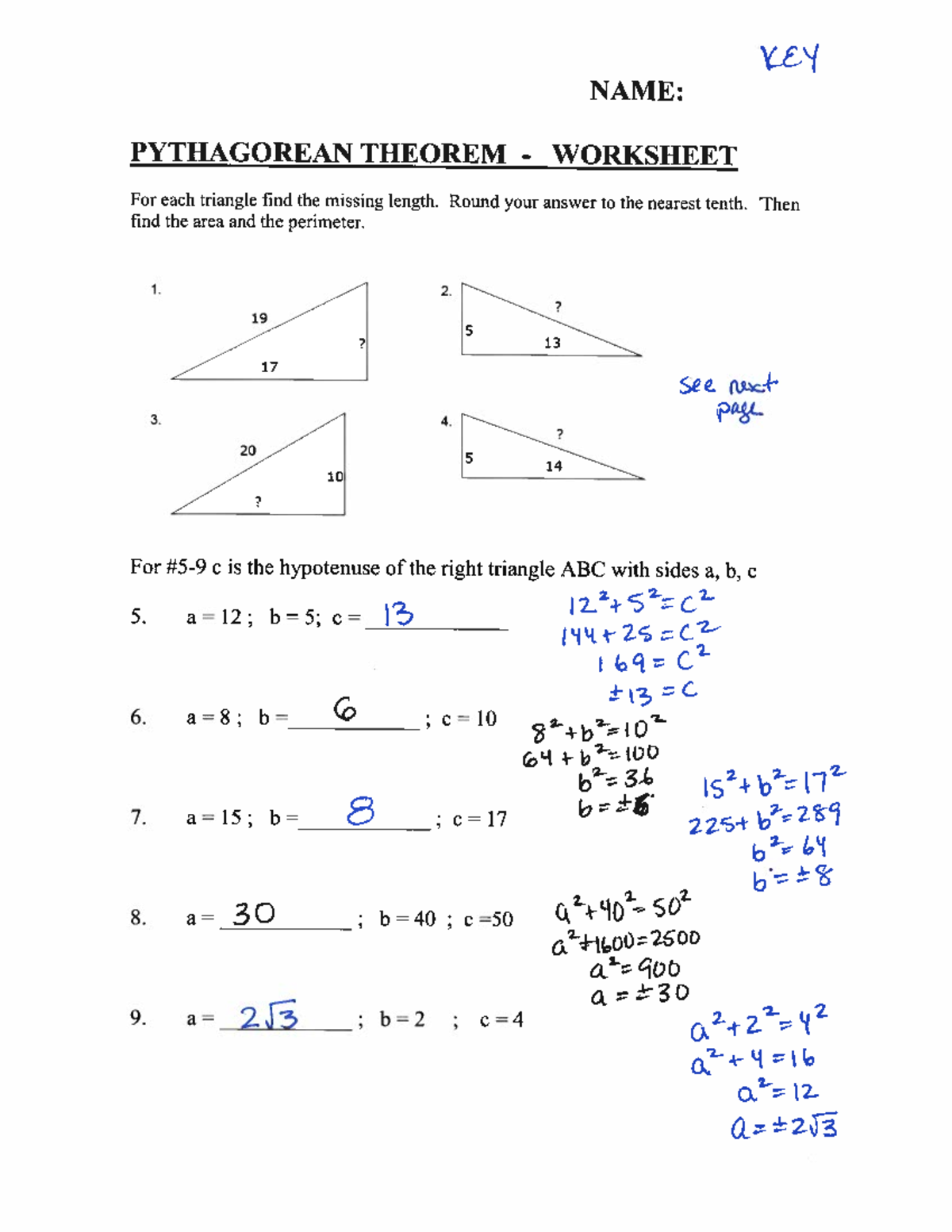
If the hypotenuse is 10 units and one leg a is 6 units, find the other leg b.
Using the theorem:
6² + b² = 10²
36 + b² = 100
b² = 100 - 36 = 64
b = √64 = 8
Problem 3

Determine if a triangle with sides 5, 12, and 13 is a right triangle.
We apply the theorem:
(5)² + (12)² = (13)²
25 + 144 = 169
169 = 169, thus, it is a right triangle.
Problem 4

Find the missing side when two sides are 6 and 9.
This triangle could have two possible configurations:
- If 9 is the hypotenuse:
6² + b² = 9²
36 + b² = 81
b² = 45
b = √45 ≈ 6.708
<li>If 9 is a leg:</li>
<p>a² + 6² = 9²</p>
<p>a² + 36 = 81</p>
<p>a² = 45</p>
<p>a = √45 ≈ 6.708</p>
Problem 5
A diagonal of a rectangle measures 15 units. One side is 9 units. Find the length of the other side.
Let's call the unknown side b:
(9)² + b² = (15)²
81 + b² = 225
b² = 225 - 81 = 144
b = √144 = 12
With these examples and quick checks, we've ensured that you have a solid understanding of how to apply the Pythagorean theorem in various scenarios. Remember, the essence of this theorem lies in its simplicity but also in its universal applicability. Whether you're designing structures, calculating distances, or simply solving geometric problems, the Pythagorean theorem is an invaluable tool. Always check your work with these quick checks, and soon, the theorem will become second nature, allowing you to solve problems with ease and precision.
What if my triangle has all sides equal?

+
If all sides are equal, you are dealing with an equilateral triangle, which does not form a right angle.
How do I know which side is the hypotenuse in a right triangle?

+
The hypotenuse is always the longest side opposite the right angle.
Is the Pythagorean theorem applicable only to right triangles?

+
Yes, the Pythagorean theorem holds true for right triangles only.
Can the Pythagorean theorem be used to find the third side when two are known?

+
Yes, if you know two sides, you can find the third side, regardless of whether it’s a leg or the hypotenuse.
What are some real-world applications of the Pythagorean theorem?

+
The theorem is used in construction for determining the right angles in structures, navigation to find distances, and in physics for force and vector analysis, to name a few.