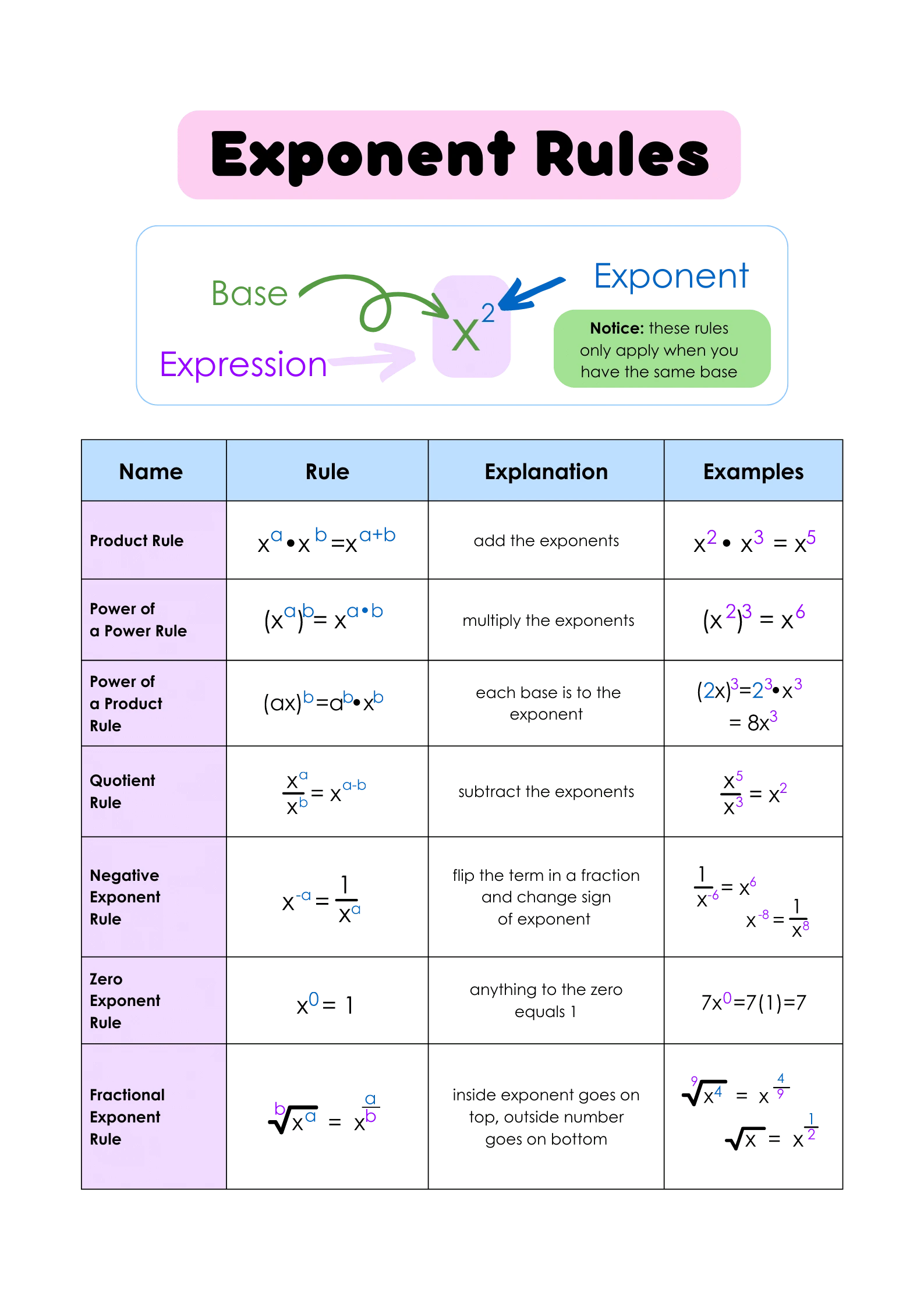
5 Essential Tips for Mastering Exponents Product Rule

Understanding exponents and how they interact with each other is fundamental in various mathematical operations, particularly when dealing with expressions involving powers and roots. The exponents product rule, one of the core rules of exponents, states that when multiplying two exponential terms with the same base, you add their exponents. This concept might seem simple, but mastering it can open up a world of mathematical problem-solving techniques. Here are five essential tips for mastering the exponent product rule:
1. Understand the Basics

Before you can master the exponents product rule, you need a firm grasp of what exponents are and how they function. An exponent represents the number of times a number, known as the base, is multiplied by itself.
- Example: (a^m \times a^n = a^{(m+n)})
2. Practice Simplification
To truly get comfortable with the exponents product rule, practice simplifying expressions. This involves recognizing when you can apply the rule and doing so efficiently.

- Example: Simplify (2^3 \times 2^4)
- Step 1: Identify the base (2) and the exponents (3 and 4).
- Step 2: Add the exponents (3 + 4 = 7).
- Result: (2^3 \times 2^4 = 2^7 = 128).
3. Apply the Rule in Complex Scenarios

After mastering basic simplification, tackle expressions where the exponents product rule interacts with other algebraic rules or when dealing with negative exponents or fractional exponents.
- Example: Solve ((x^3 \times x^{-2})^{-1})
- Step 1: Apply the exponents product rule first (3 + (-2) = 1).
- Step 2: Apply the power of a product rule for the exponent outside the bracket.
- Result: ((x^3 \times x^{-2})^{-1} = x^{1}^{-1} = x^{-1} = \frac{1}{x}).
4. Connect with Other Exponential Properties

The exponents product rule doesn’t exist in isolation. It often works alongside other rules like the power of a product rule, power of a quotient rule, and negative exponents rule. Understanding how these properties connect can simplify complex calculations.
🔍 Note: When dealing with negative exponents, keep in mind that raising a term to a negative exponent is equivalent to the reciprocal of the term raised to the positive exponent.
5. Use Mnemonics for Memory and Application

Creating mnemonics can aid in memorizing the exponents product rule and its application. For example:
- “Add the Power, Keep the Base:” This phrase reminds you to add the exponents while keeping the base unchanged.
By now, you're equipped with the foundational understanding and practical techniques to confidently apply the exponents product rule. Whether simplifying basic expressions or tackling more complex problems, these tips will help you navigate through the realm of exponents with ease and precision. As you continue to practice, you'll find that your intuition for algebraic operations involving exponents will grow, turning what once might have been a daunting task into an intuitive part of your mathematical toolkit.
Why is it important to master the exponents product rule?

+
Mastering the exponents product rule simplifies algebraic manipulations, making complex calculations more manageable and efficient. It is essential in calculus, physics, engineering, and other fields where exponentiation is prevalent.
How does the exponents product rule relate to other exponent rules?

+
The exponents product rule often works in conjunction with other rules such as the power of a product rule, power of a quotient rule, and negative exponents rule, allowing for comprehensive manipulation of expressions involving exponents.
Can the exponents product rule be applied if the bases are different?
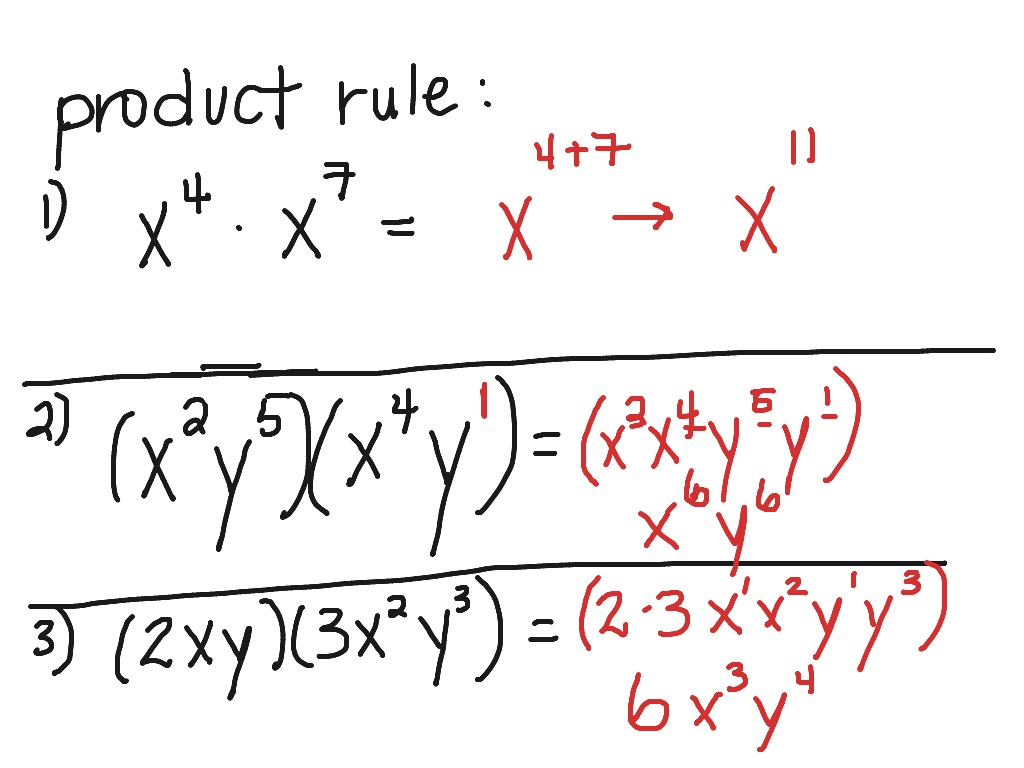
+
No, the exponents product rule only applies when the bases are the same. When the bases differ, you might need to simplify each term first or use logarithms to manipulate the expressions before applying the rule.