Pythagorean Theorem: Easily Find Missing Sides Worksheet

Introduction to the Pythagorean Theorem

The Pythagorean theorem is one of the most fundamental principles in Euclidean geometry, providing a valuable tool for various calculations, especially in right-angled triangles. Whether you’re a student navigating through high school geometry or an enthusiast in mathematics, understanding this theorem can significantly enhance your problem-solving skills.

In this comprehensive guide, we’ll delve into the origins, applications, and step-by-step methods for using the Pythagorean theorem to find missing sides in a triangle.
What is the Pythagorean Theorem?

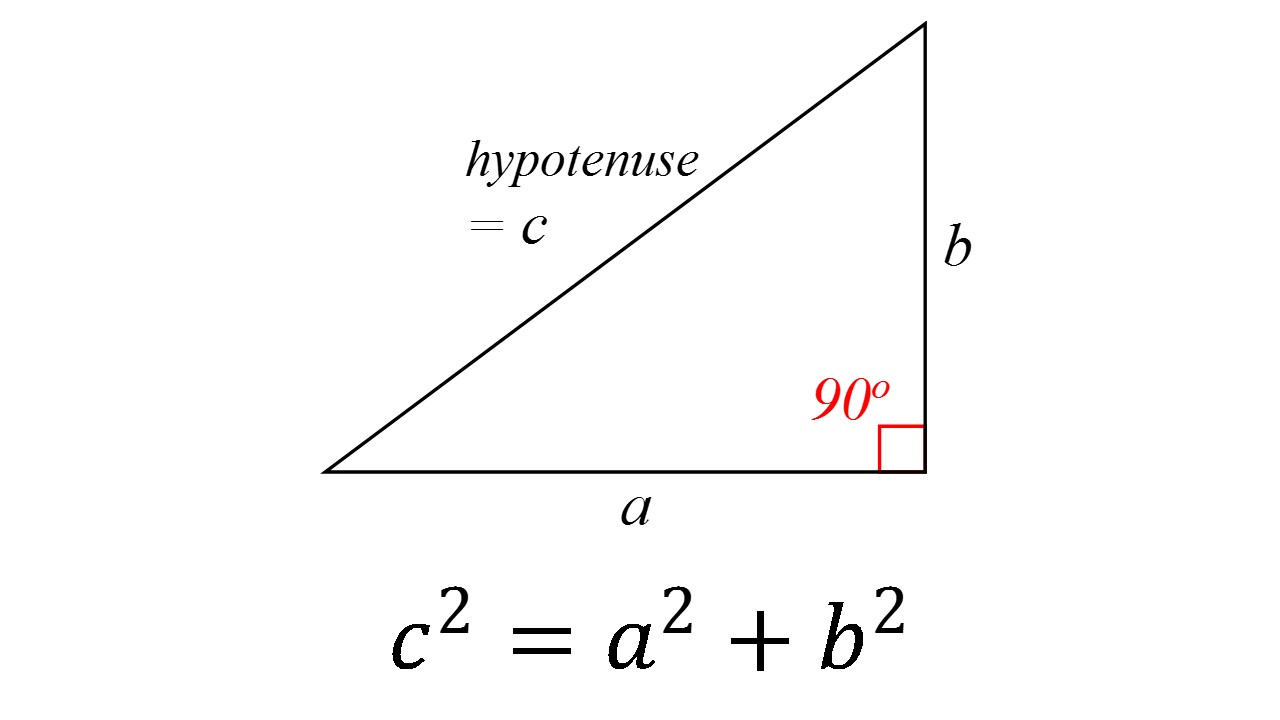
The Pythagorean theorem states that in any right-angled triangle:
- The square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Mathematically, it’s expressed as:
a2 + b2 = c2
Here, a and b are the lengths of the legs (the shorter sides), and c is the length of the hypotenuse.
History and Significance
Although named after the ancient Greek philosopher Pythagoras, historians debate whether he was the original author of this theorem. Nonetheless, his name has been associated with it since antiquity due to his work in establishing the principle. The theorem was known long before Pythagoras, with evidence of its use in ancient Indian, Chinese, and Babylonian cultures.
The significance of the Pythagorean theorem extends beyond mathematics:
- It’s applied in construction, engineering, computer graphics, and even in physical theories such as quantum mechanics.
- The theorem proves that for any right-angled triangle, there’s a unique relationship between its sides, which forms the basis for trigonometry.
Practical Applications

Here are some practical applications where the Pythagorean theorem is essential:
- Construction and Architecture: To ensure buildings are level or to cut materials at precise angles.
- Land Surveying: To calculate distances across obstacles or over rough terrain.
- Navigation: Pilots and sailors use it to determine shortest paths over the Earth’s surface.
Finding Missing Sides

When Both Legs are Known

Given the lengths of the legs a and b, you can find the hypotenuse c by using:
c = √(a2 + b2)
Example:
- If a = 3 and b = 4, then
- c = √(32 + 42) = √25 = 5
When One Leg and the Hypotenuse are Known

If you know one leg and the hypotenuse, to find the other leg, rearrange the equation:
a = √(c2 - b2) or b = √(c2 - a2)
Example:
- If c = 5 and a = 3, then
- b = √(52 - 32) = √16 = 4
🔍 Note: Always ensure you are working with the correct relationship between the sides; the hypotenuse is always the longest side.
When Only the Hypotenuse is Known
If you only know the hypotenuse, you can’t directly find the other sides, but you can explore possible integer solutions or use trigonometric ratios for more complex calculations.
Example:
- For c = 5, possible integer values for a and b could be 3 and 4, or 1 and √24 (which isn’t an integer).
Exercises and Worksheet

Here’s a simple worksheet to practice applying the Pythagorean theorem:
| Problem | Solution |
|---|---|
| Find c if a = 6 and b = 8. | c = 10 |
| Find a if b = 5 and c = 13. | a ≈ 12 |
| Is a triangle with sides 9, 40, and 41 a right triangle? | Yes |
| Find c if a = 12 and b = 5. | c = 13 |
| Find b if a = 9 and c = 15. | b ≈ 12 |

Summary

The Pythagorean theorem remains a cornerstone in geometry with broad applications. By mastering this theorem, you can solve problems involving right triangles with ease. Whether you’re calculating distances or designing structures, the ability to find missing sides with the Pythagorean theorem can provide practical and theoretical insights.
Who discovered the Pythagorean theorem?

+
The theorem was known to several ancient cultures before Pythagoras, although it’s commonly named after him due to his contributions to its proof and broader application.
Can the Pythagorean theorem be used for any triangle?

+
No, it applies specifically to right-angled triangles. However, its principles can be extended or modified for other types of triangles through more advanced geometry.
What are the common mistakes when applying the Pythagorean theorem?

+
The most common mistake is misidentifying which side is the hypotenuse. Remember, the hypotenuse is always the longest side in a right triangle, opposite the right angle.