5 Tips for Solving Parallel Lines Worksheets

🌟 Note: This content piece employs an educational framework designed to enhance the understanding of parallel lines, geometry, and problem-solving techniques in math worksheets.
Understanding Parallel Lines and Their Importance in Geometry
Parallel lines are lines in a plane that do not intersect or touch each other at any point. In the realm of geometry, these lines have particular significance because they are pivotal in understanding the properties and relationships of other geometric shapes and figures. Whether you’re a student dealing with parallel lines worksheets or someone interested in the foundations of geometric design, recognizing the properties of parallel lines can significantly enhance your grasp on various spatial relationships.
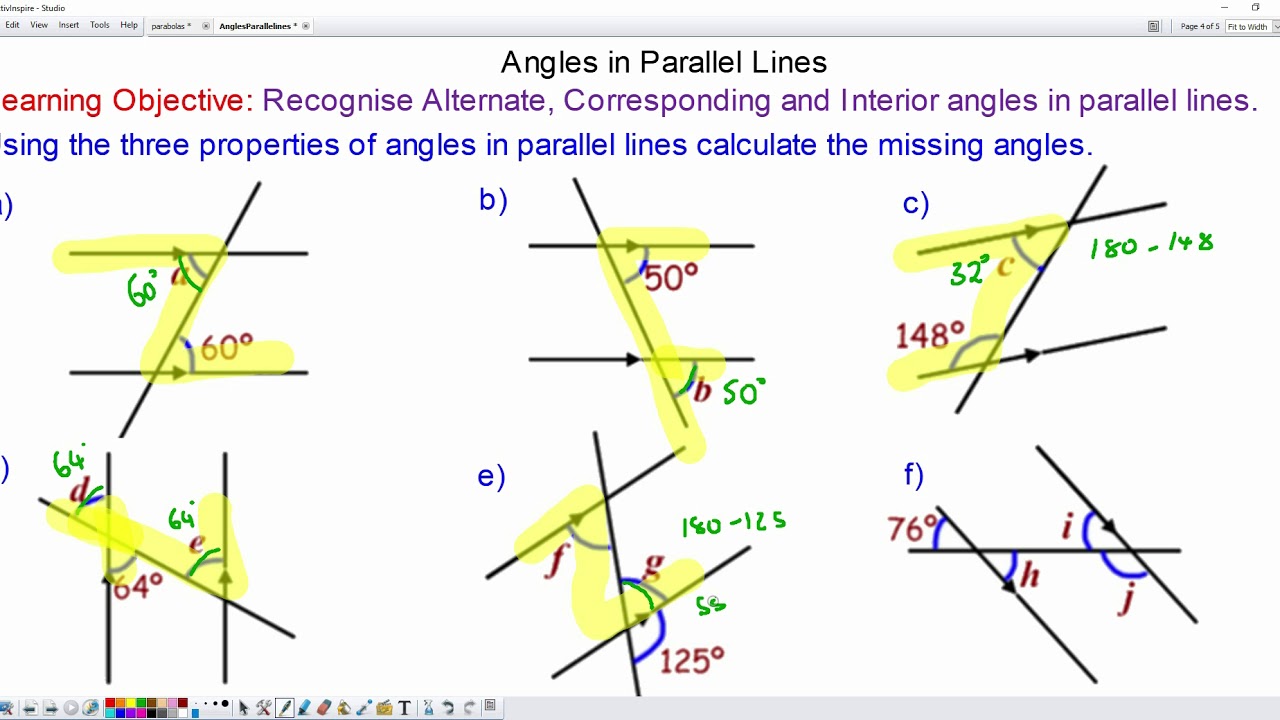
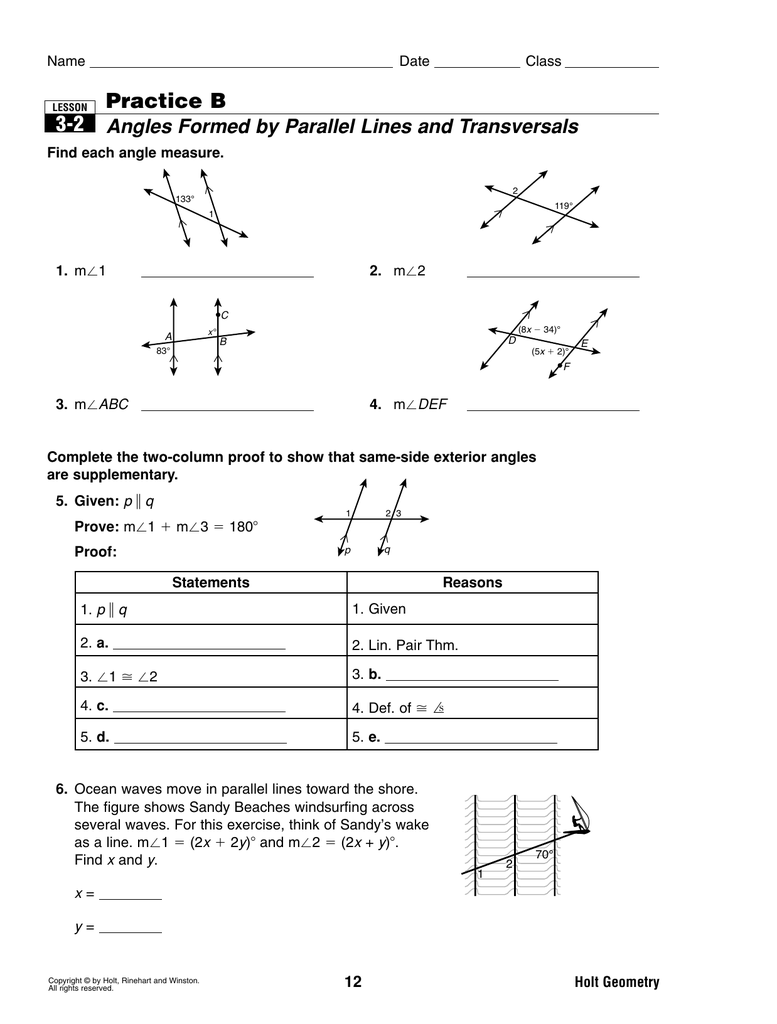
Tip 1: Identify Corresponding, Alternate Interior, and Consecutive Interior Angles

When dealing with parallel lines cut by a transversal, the angles formed can be grouped into several types:
- Corresponding Angles: These are pairs of angles that are in the same relative position at the intersection of a line and two others, like ∠A and ∠E in the diagram below.
- Alternate Interior Angles: These are on opposite sides of the transversal and between the two lines, like ∠D and ∠E.
- Consecutive Interior Angles: These are on the same side of the transversal and between the two lines, like ∠D and ∠F.

Tip 2: Use the Transversal Angles Theorem

The Transversal Angles Theorem, also known as the Alternate Interior Angle Theorem, states that if a transversal intersects two parallel lines, then the alternate interior angles are congruent. This theorem can be your shortcut to solving parallel lines worksheets efficiently. When you see pairs like ∠D and ∠E, you know they’re equal, making other angle relationships easier to calculate.
Tip 3: Master the 180-Degree Rule for Consecutive Interior Angles

Consecutive interior angles on the same side of the transversal between parallel lines always add up to 180 degrees. Understanding this rule allows you to:
- Find a missing angle when one consecutive angle is given.
- Confirm whether lines are parallel by checking if the sum of consecutive interior angles equals 180 degrees.
🧠 Note: This rule can be particularly helpful in complex geometry problems where angles interact in multiple ways.
Tip 4: Pay Attention to Vertical Angles

Vertical angles are the angles opposite each other when two lines intersect. They have the property of being equal in measure. When working with parallel lines cut by a transversal, these angles can sometimes be overlooked, but they often hold the key to quickly solving problems on your parallel lines worksheets:
| Angle Type | Angle Pairs | Equal To |
|---|---|---|
| Vertical | ∠A, ∠B | ∠C, ∠D |
| Vertical | ∠E, ∠F | ∠G, ∠H |

Tip 5: Utilize Parallel Lines and Coordinate Geometry
In coordinate geometry, parallel lines have the same slope. This relationship can be leveraged to verify parallelism:
- Given two lines with equations y = mx + b and y = nx + c, if m = n, the lines are parallel.
- Using the slope formula, you can derive this information from coordinate pairs or points on the line.
🌍 Note: The concept of slope extends beyond paper and pencil into real-world applications like architecture, engineering, and geographic analysis.
Equipped with these tips, parallel lines worksheets should become a more manageable task. By understanding the fundamental theorems and properties of parallel lines, you'll not only solve problems more efficiently but also appreciate the beauty of geometry in our environment and daily life.
Key Takeaways:
- Identify and use angle relationships to quickly solve for unknowns.
- Use theorems like the Transversal Angles Theorem to deduce angles.
- Remember that consecutive interior angles form straight lines.
- Vertical angles are your friends in parallel line problems.
- Apply coordinate geometry for an analytical approach to parallelism.
Why are parallel lines important in geometry?

+
Parallel lines establish the foundation for understanding many spatial relationships, making them essential in both theoretical geometry and its practical applications.
Can two non-parallel lines ever have the same slope?

+
No, two non-parallel lines always have different slopes. If two lines share the same slope, they must be parallel.
What if I get confused with angle naming in parallel lines problems?

+
Use visual aids like diagrams to label angles clearly. Relate angles to known theorems or properties, and work backward from what you do know to find the unknown.



