5 Proven Methods to Prove Lines Parallel Easily

In geometry, understanding the concept of parallel lines is crucial for tackling various geometric proofs and problems. While proving lines are parallel might initially seem daunting, several methods simplify this process, making it straightforward and logical. This blog post outlines five proven methods to prove lines parallel, helping students and enthusiasts alike to grasp this fundamental geometry principle with ease.
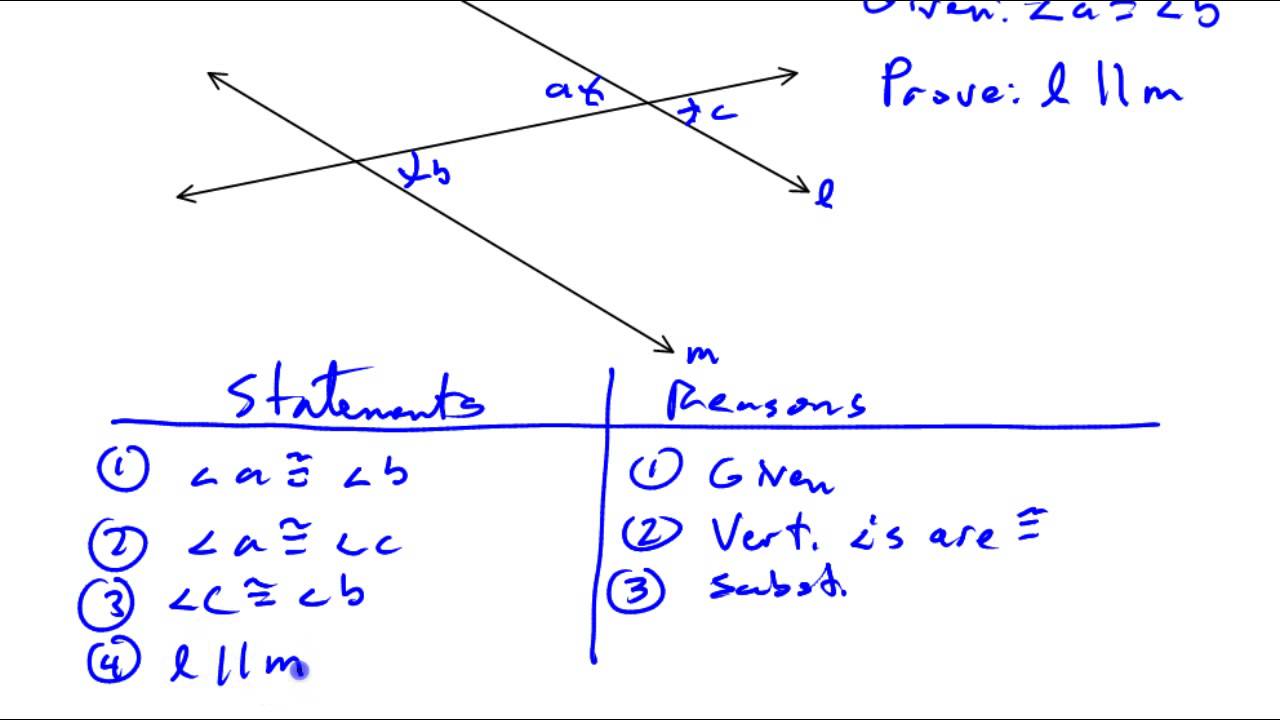
Method 1: Transversal and Corresponding Angles

If a transversal intersects two lines, making a pair of corresponding angles equal, then the lines are parallel. Here’s how:
- Identify the transversal: This is a line that cuts through the two lines at different points.
- Find corresponding angles: These are the angles that lie on the same side of the transversal, in the same relative positions (for example, both angles could be above the lines, or both could be below).
- Prove the angles equal: If you can show that any pair of corresponding angles are equal, the lines are parallel.
🌟 Note: Remember, corresponding angles are congruent when lines are parallel. This relationship is often used in both direction of proving.
Method 2: Alternate Interior Angles

When a transversal cuts two lines and the alternate interior angles (angles on opposite sides of the transversal, inside the two lines) are equal, the lines are parallel. Here’s how to use this method:
- Spot the alternate interior angles: These are angles that do not share a side with the transversal and are inside the lines.
- Prove these angles are equal: If you can demonstrate the equality of any pair of alternate interior angles, you can assert the lines are parallel.
Method 3: Same-Side Interior Angles

This method involves the same-side interior angles, which are on the same side of the transversal, inside the lines. Here’s the approach:
- Identify the angles: Look for angles that are on the same side of the transversal and inside the lines.
- Establish their supplementary nature: If these angles sum up to 180 degrees, the lines are parallel.
Method 4: Converse of the Perpendicular Transversal Theorem

According to this theorem, if two lines are perpendicular to the same line, then they are parallel to each other. Here’s how you can apply it:
- Find lines perpendicular to a common line: If you have two lines that are both perpendicular to a third line, this third line is the transversal.
- Conclude parallelism: Since both lines are perpendicular to the same line, they must be parallel.
Method 5: Triangle Congruence Criteria

Using triangle congruence can also help prove lines parallel. Here are some steps:
- Construct triangles: Form triangles where one of the sides is a segment of the lines you want to prove parallel.
- Prove triangles congruent: If you can show that these triangles are congruent using criteria like SAS, ASA, or SSS, and the corresponding sides or angles are parallel, then the lines are parallel.
These five methods offer a variety of approaches for proving lines parallel, each catering to different geometric situations. Whether through angles, perpendicularity, or triangle congruence, understanding and applying these methods can significantly enhance your geometrical skills and problem-solving abilities.
Can two lines be parallel without any transversal?

+
No, in classical Euclidean geometry, to prove lines are parallel, a transversal or some indirect proof through perpendicular lines is usually necessary.
Do I always need to prove angles are congruent to show lines are parallel?

+
Not always. While angles are commonly used, methods like the converse of the perpendicular transversal theorem do not involve angles directly.
What are some real-world applications of parallel lines?

+
Parallel lines are used in road designs, ensuring lanes run alongside each other without intersecting. They also play a role in construction, particularly in ensuring walls are vertical and surfaces are level.
How can one verify if lines are truly parallel in practical scenarios?
+
Practically, you can use tools like a level, a straightedge, or a theodolite for more precise measurements to ensure lines are parallel.



