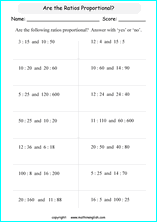
Proportional Reasoning Worksheet: Unlock Math Mastery Today

Introduction to Proportional Reasoning

Proportional reasoning is a cornerstone of mathematical understanding, offering a gateway to mastering advanced concepts. This skill allows students to understand and analyze relationships between quantities, making it essential in fields ranging from science and engineering to finance and daily life decision-making. This proportional reasoning worksheet aims to unlock the potential for math mastery, providing structured practice that enhances comprehension and application.

Understanding Proportionality

Before diving into the worksheet, let’s grasp the basics of proportionality:
- Direct Proportionality: When two quantities increase or decrease together, they are directly proportional. If one doubles, so does the other.
- Inverse Proportionality: Here, as one quantity increases, the other decreases, maintaining their product as constant.
This knowledge forms the basis of our proportional reasoning worksheet, which helps students discern these relationships and apply them accurately.
Setting Up Proportions

The setup of proportions is crucial. Here’s how you can guide students through this process:
- Identify the Known: Establish the given quantities. For example, if 3 apples cost 6, how much would 5 apples cost?</li> <li><strong>Set Up the Equation:</strong> Use the proportion 3/6 = 5/x, where 'x' is the cost of 5 apples.</li> <li><strong>Solve for Unknown:</strong> Cross-multiply and solve to find x. Here, x = (3/6) * 5 = 10.
Practical Applications

Here’s where we apply theory to real-world scenarios:
| Scenario | Direct Proportion | Inverse Proportion |
|---|---|---|
| Distance covered by car at constant speed | Increase in distance with increase in time | Speed inversely proportional to travel time for a fixed distance |
| Buying eggs | More money spent for more eggs | If quantity of eggs is constant, price per egg decreases as the total number of eggs increases |

This proportional reasoning worksheet includes such scenarios to illustrate the relevance of these concepts.
📝 Note: Encouraging students to think through the steps of setting up proportions can greatly enhance their problem-solving skills.
Challenges and Strategies

Some common challenges students face in understanding proportions include:
- Difficulty in setting up the correct proportion equation.
- Misinterpreting direct and inverse relationships.
- Errors in cross-multiplication or division.
Here are strategies to overcome these:
- Practice with Visuals: Use diagrams or graphical representations to show relationships.
- Consistent Terminology: Reinforce terms like ‘direct’ and ‘inverse’ to clarify concepts.
- Worksheet Variability: Include problems that require different problem-solving approaches to keep learners engaged.
Advancing Beyond the Basics

Once students are comfortable with basic proportionality, they can explore:
- Joint Proportions: When a quantity depends on multiple other quantities.
- Variation Functions: Understanding how changes in one variable affect others.
- Modeling with Proportions: Use real data to create proportional models.
The proportional reasoning worksheet designed here can gradually introduce these advanced topics, building on foundational skills.
As we wrap up our journey through the realm of proportional reasoning, remember that this is not just about solving math problems; it's about unlocking a way of thinking that helps in making sense of the world. Whether it's understanding the relationship between speed and travel time or predicting how changes in quantities affect others, the ability to reason proportionally equips students with a powerful tool for analysis. This proportional reasoning worksheet is crafted to guide learners from basic understanding to more complex applications, fostering an environment where math mastery is not just possible but genuinely exciting.
Why is proportional reasoning important in math?

+
Proportional reasoning underpins many mathematical concepts and helps in understanding relationships between quantities, which is crucial in algebra, geometry, and various practical applications in science and engineering.
What are some common mistakes students make with proportions?
+
Students often mix up direct and inverse proportions or fail to correctly set up proportion equations, leading to errors in cross-multiplication or solving for unknown variables.
Can proportional reasoning help with word problems?

+
Absolutely! Many word problems in math require the application of proportional reasoning to solve for unknown quantities based on given relationships.
How can I make learning proportional reasoning fun for students?

+
Incorporate real-life scenarios, interactive games, visual aids, and relatable challenges into your lessons. Using technology like online simulations or educational apps can also make the learning process more engaging.
What are the next steps after mastering basic proportional reasoning?

+
Next steps could include exploring joint proportions, variation functions, and using proportional reasoning to model real-world data, which introduces students to more complex mathematical modeling and problem-solving.