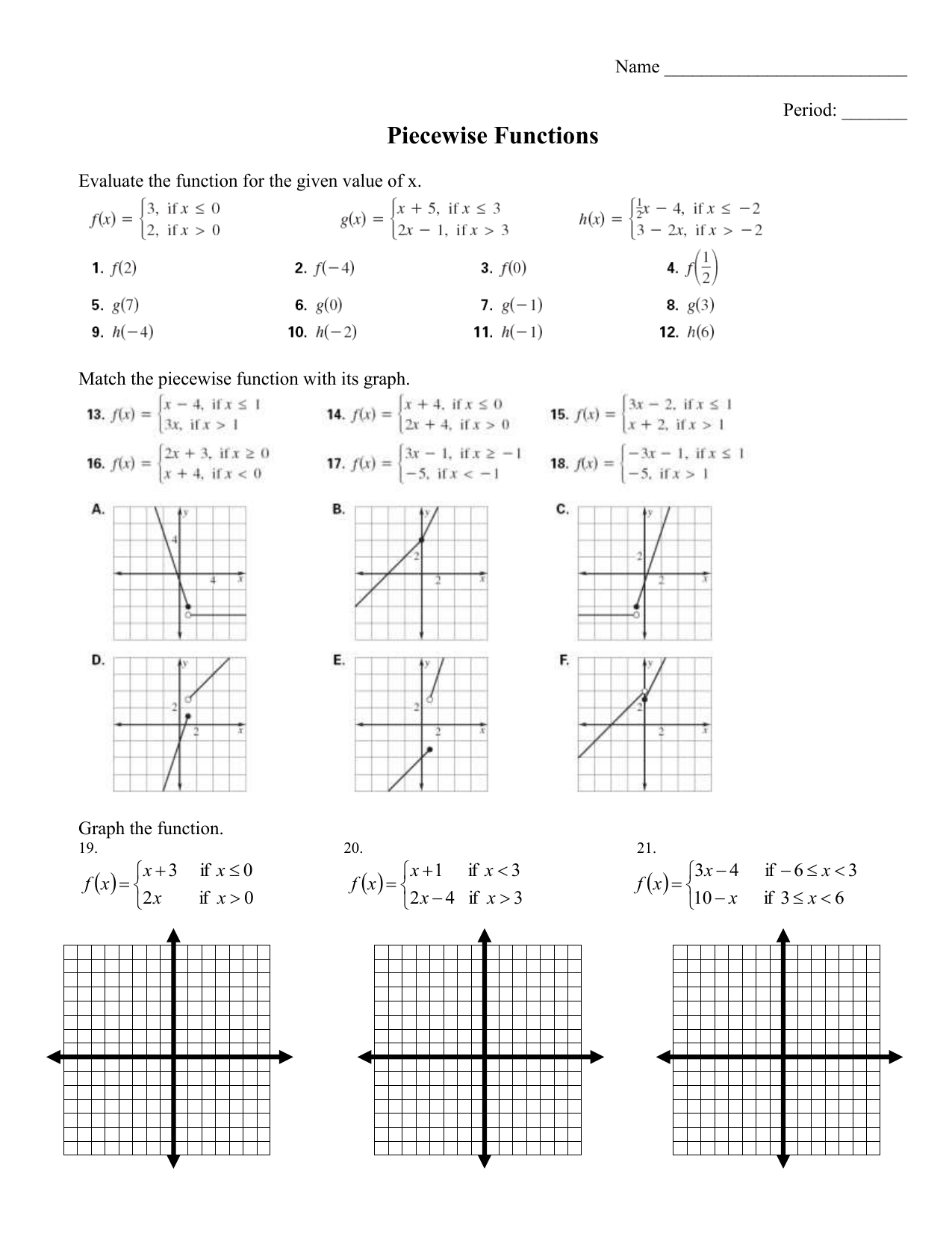
Quadratic Functions Worksheet: Key Properties and Insights
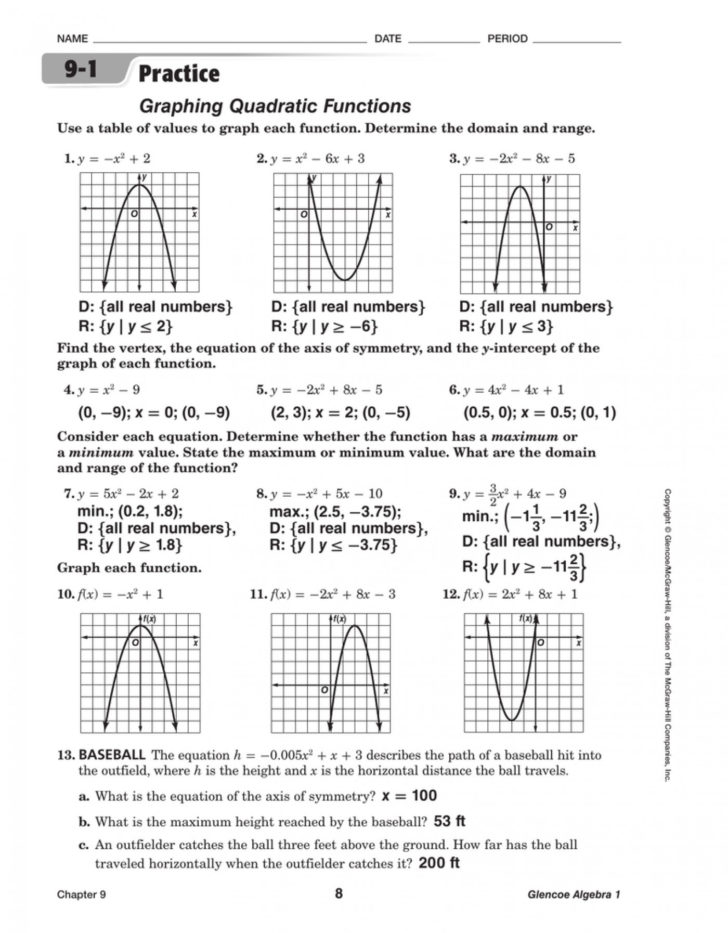
In the fascinating universe of algebra, quadratic functions stand out as one of the fundamental topics that many students encounter. Whether you're delving into the world of parabolas, learning how to solve quadratic equations, or analyzing the nature of quadratic graphs, understanding these key properties provides you with a solid foundation in mathematics. This blog post aims to enhance your grasp of quadratic functions by exploring their definitions, properties, and some insightful applications.
Introduction to Quadratic Functions


A quadratic function can be defined by the general formula:
f(x) = ax2 + bx + c, where a, b, and c are constants with a ≠ 0. This equation represents a parabola when graphed in the coordinate plane. Understanding the shape, direction, and key features of this parabola is crucial:
- The parabola opens upwards if a > 0 and downwards if a < 0.
- The vertex or the highest/lowest point of the parabola can be found using the formula x = -b/2a.
- The y-intercept occurs when x = 0, hence f(0) = c.
- The axis of symmetry is a vertical line passing through the vertex.
Solving Quadratic Equations


There are several methods to solve quadratic equations, each with its own advantages:
- Factoring: Split the equation into factors where each factor equals zero.
- Completing the Square: This technique helps by transforming the quadratic into a perfect square trinomial.
- Quadratic Formula: Widely applicable, this formula is given by x = [-b ± √(b² - 4ac)] / 2a.
- Graphing: Visual approach where you can approximate or find exact solutions by plotting the function.
Each method has its context where it shines, depending on the coefficients and structure of the quadratic equation.
Key Properties of Quadratic Functions
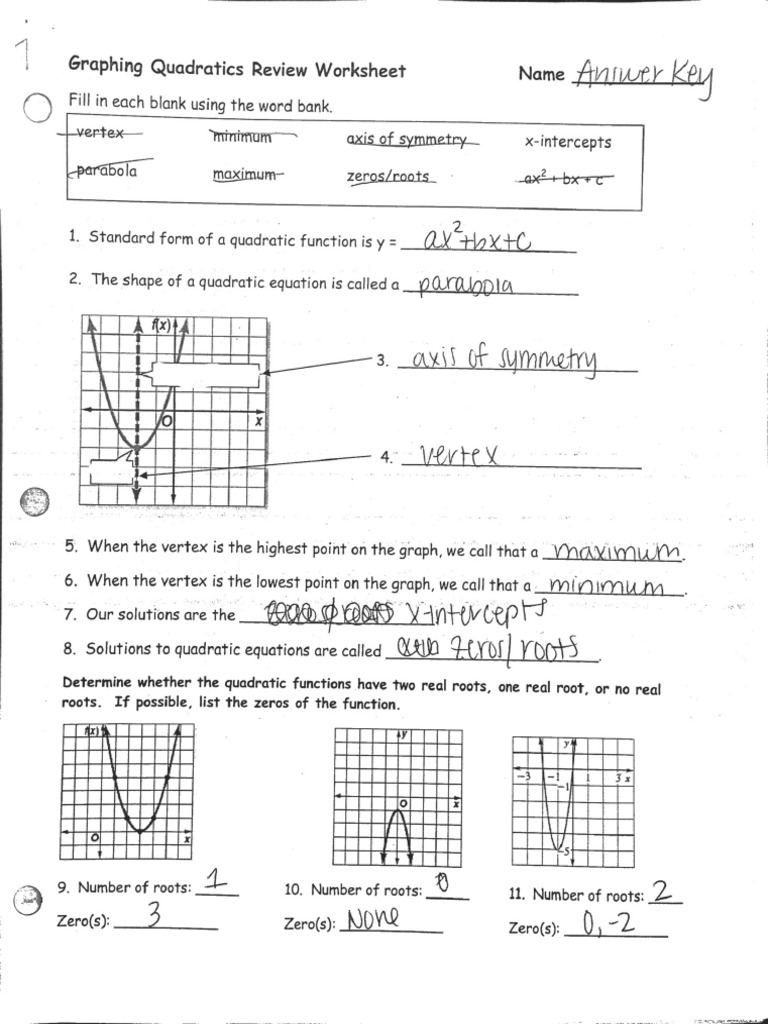

When analyzing quadratic functions, several properties help us understand their behavior:
- Vertex Form: A function in the form f(x) = a(x - h)² + k where (h, k) are the coordinates of the vertex.
- Discriminant: b² - 4ac dictates the nature of the roots:
- If > 0, two distinct real roots.
- If = 0, one real root (or two identical roots).
- If < 0, no real roots (complex conjugate pairs).
- Range: For a quadratic with a > 0, the range is [k, ∞); for a < 0, it’s (-∞, k].
- End Behavior: As x approaches positive or negative infinity, the function either increases or decreases without bound.
Applications of Quadratic Functions


Quadratic functions are not just theoretical constructs; they have real-world implications:
- Projectile Motion: Predicting the path of a ball thrown in the air.
- Optimization Problems: Finding maximum or minimum values in economic or design scenarios.
- Geometry: Calculating areas or solving problems involving lengths.
- Electrical Engineering: Analyzing the behavior of circuits.
Important Notes

💡 Note: The quadratic formula can simplify complex problems, but remember that not all real-world problems can be modeled perfectly by a quadratic function.
By grasping these key properties, we not only enhance our mathematical skills but also open the door to a deeper understanding of how mathematical concepts can describe and predict real-world phenomena. Understanding the shape, roots, and behavior of quadratic functions provides insights into physics, finance, engineering, and beyond. It's a testament to the power of mathematical modeling in everyday life.
What is the significance of the discriminant in a quadratic equation?

+
The discriminant, b² - 4ac, tells us the nature of the roots of a quadratic equation. If it’s positive, you get two distinct real roots; if it’s zero, one real root; if it’s negative, you get complex conjugate pairs.
How do you find the vertex of a quadratic function?
+
The vertex can be found using the formula x = -b / 2a. Plug this value back into the function to find the corresponding y-coordinate.
Can quadratic functions have negative coefficients?

+
Yes, but note that if a (the coefficient of x²) is negative, the parabola opens downwards; if positive, it opens upwards.
What does a negative discriminant indicate?
+
A negative discriminant indicates that the quadratic equation does not have real roots; instead, the solutions are complex numbers.
Why is the vertex form of a quadratic function important?

+
The vertex form f(x) = a(x - h)² + k reveals the vertex of the parabola directly, making it easy to see the minimum or maximum value of the function without solving for it.