5 Key Properties of Numbers You Need to Know
Understanding the Fundamentals of Numbers

Numbers are an essential part of mathematics, and understanding their properties is crucial for solving various mathematical problems. In this article, we will explore five key properties of numbers that you need to know. These properties are the foundation of arithmetic operations and are used extensively in algebra, geometry, and other branches of mathematics.
1. Commutative Property of Addition and Multiplication

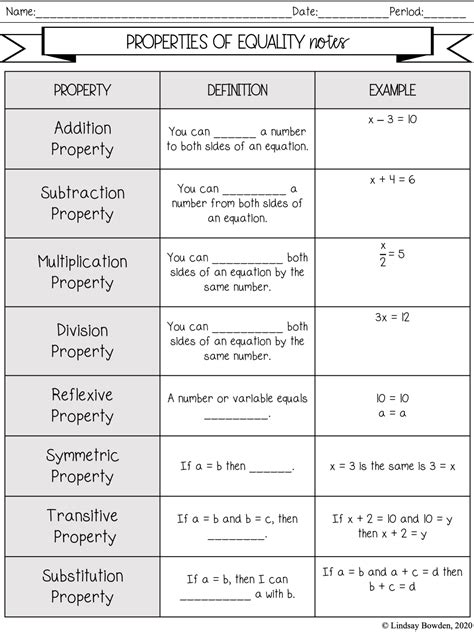
The commutative property of addition and multiplication states that the order of the numbers does not change the result of the operation. In other words, if you add or multiply two numbers, the result will be the same regardless of the order in which you perform the operation.
Commutative Property of Addition: a + b = b + a
Commutative Property of Multiplication: a × b = b × a
For example, 2 + 3 = 3 + 2 = 5 and 4 × 5 = 5 × 4 = 20.
📝 Note: This property only applies to addition and multiplication, not to subtraction and division.
2. Associative Property of Addition and Multiplication

The associative property of addition and multiplication states that when you perform an operation on three or more numbers, the order in which you perform the operation does not change the result.
Associative Property of Addition: (a + b) + c = a + (b + c)
Associative Property of Multiplication: (a × b) × c = a × (b × c)
For example, (2 + 3) + 4 = 2 + (3 + 4) = 9 and (4 × 5) × 2 = 4 × (5 × 2) = 40.
3. Distributive Property of Multiplication over Addition

The distributive property of multiplication over addition states that when you multiply a number by the sum of two or more numbers, you can distribute the multiplication to each number separately.
Distributive Property: a × (b + c) = a × b + a × c
For example, 3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15 = 27.
4. Identity Property of Addition and Multiplication

The identity property of addition and multiplication states that there is a number that, when added to or multiplied by another number, does not change the result.
Identity Property of Addition: a + 0 = a
Identity Property of Multiplication: a × 1 = a
For example, 5 + 0 = 5 and 6 × 1 = 6.
5. Inverse Property of Addition and Multiplication

The inverse property of addition and multiplication states that there is a number that, when added to or multiplied by another number, results in the identity number.
Inverse Property of Addition: a + (-a) = 0
Inverse Property of Multiplication: a × (1/a) = 1
For example, 5 + (-5) = 0 and 6 × (1⁄6) = 1.
Understanding these five key properties of numbers is essential for building a strong foundation in mathematics. By mastering these properties, you will be able to solve various mathematical problems with ease and confidence.
Without these properties, mathematics would be a very different and much more complicated subject. By understanding how numbers work and interact with each other, you can unlock the secrets of mathematics and develop a deeper appreciation for the subject.
What is the commutative property of addition?

+
The commutative property of addition states that the order of the numbers does not change the result of the operation. For example, 2 + 3 = 3 + 2 = 5.
What is the distributive property of multiplication over addition?

+
The distributive property of multiplication over addition states that when you multiply a number by the sum of two or more numbers, you can distribute the multiplication to each number separately. For example, 3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15 = 27.
What is the identity property of multiplication?

+
The identity property of multiplication states that there is a number that, when multiplied by another number, does not change the result. For example, 6 × 1 = 6.
Related Terms:
- Teacher synergy llc
- Khan Academy
- IXL Learning
- Quizlet
- BrainPop
- Udacity