5 Essential Properties of Exponents to Master Now

Unlocking the Power of Exponents: 5 Essential Properties to Master

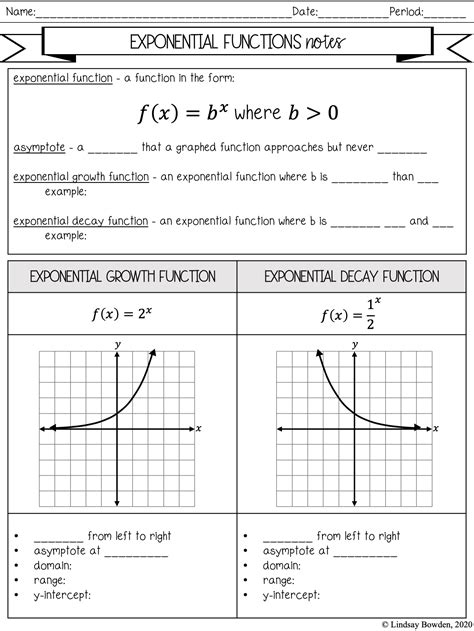
Exponents are a fundamental concept in mathematics, and understanding their properties is crucial for solving equations, manipulating expressions, and modeling real-world phenomena. In this article, we will delve into the 5 essential properties of exponents that you need to master to become proficient in mathematics.
Property 1: Product of Powers

The product of powers property states that when you multiply two exponential expressions with the same base, you add their exponents. Mathematically, this can be represented as:
am × an = am+n
For example:
23 × 24 = 23+4 = 27
This property helps simplify complex expressions and is a building block for more advanced exponent properties.
Property 2: Power of a Power

The power of a power property states that when you raise an exponential expression to another power, you multiply the exponents. Mathematically, this can be represented as:
(am)n = am×n
For example:
(23)4 = 23×4 = 212
This property is essential for working with nested exponential expressions.
Property 3: Power of a Product

The power of a product property states that when you raise a product of exponential expressions to a power, you raise each factor to that power. Mathematically, this can be represented as:
(ab)m = ambm
For example:
(2 × 3)4 = 24 × 34
This property helps simplify expressions involving products of exponential terms.
Property 4: Zero Exponent

The zero exponent property states that any non-zero number raised to the power of zero is equal to 1. Mathematically, this can be represented as:
a0 = 1
For example:
20 = 1
This property may seem trivial, but it is crucial for simplifying expressions and avoiding division by zero errors.
Property 5: Negative Exponent
The negative exponent property states that a negative exponent is equivalent to the reciprocal of the same base raised to the positive exponent. Mathematically, this can be represented as:
a-m = 1/am
For example:
2-3 = 1⁄23
This property helps simplify expressions involving negative exponents and is essential for working with rational expressions.
📝 Note: These properties can be combined and applied in various ways to simplify complex expressions and solve equations.
| Property | Mathematical Representation | Example |
|---|---|---|
| Product of Powers | am × an = am+n | 23 × 24 = 27 |
| Power of a Power | (am)n = am×n | (23)4 = 212 |
| Power of a Product | (ab)m = ambm | (2 × 3)4 = 24 × 34 |
| Zero Exponent | a0 = 1 | 20 = 1 |
| Negative Exponent | a-m = 1/am | 2-3 = 1/23 |

By mastering these 5 essential properties of exponents, you will become proficient in working with exponential expressions and be able to tackle complex mathematical problems with confidence.
In summary, the key takeaways from this article are the 5 essential properties of exponents: product of powers, power of a power, power of a product, zero exponent, and negative exponent. These properties are the building blocks of exponent manipulation and are crucial for solving equations and modeling real-world phenomena. By applying these properties, you will become proficient in working with exponential expressions and be able to tackle complex mathematical problems with confidence.
What is the product of powers property?

+
The product of powers property states that when you multiply two exponential expressions with the same base, you add their exponents.
How do you simplify expressions involving negative exponents?

+
A negative exponent is equivalent to the reciprocal of the same base raised to the positive exponent.
What is the power of a power property?

+
The power of a power property states that when you raise an exponential expression to another power, you multiply the exponents.
Related Terms:
- Properties of Exponents Worksheet PDF
- Properties of Exponents pdf
- simplify properties of exponents practice
- properties of exponents practice pdf
- free printable exponent worksheets
- properties of exponential functions worksheet