5 Must-Know Properties of Kites for Geometry Success

Understanding the properties of kites is fundamental for anyone delving into geometry. A kite, a quadrilateral known for its distinct symmetry and shape, possesses several unique characteristics that not only define its structure but also unlock doors to numerous geometric problems and theorems. Let's explore the must-know properties of kites that are crucial for your geometry success.
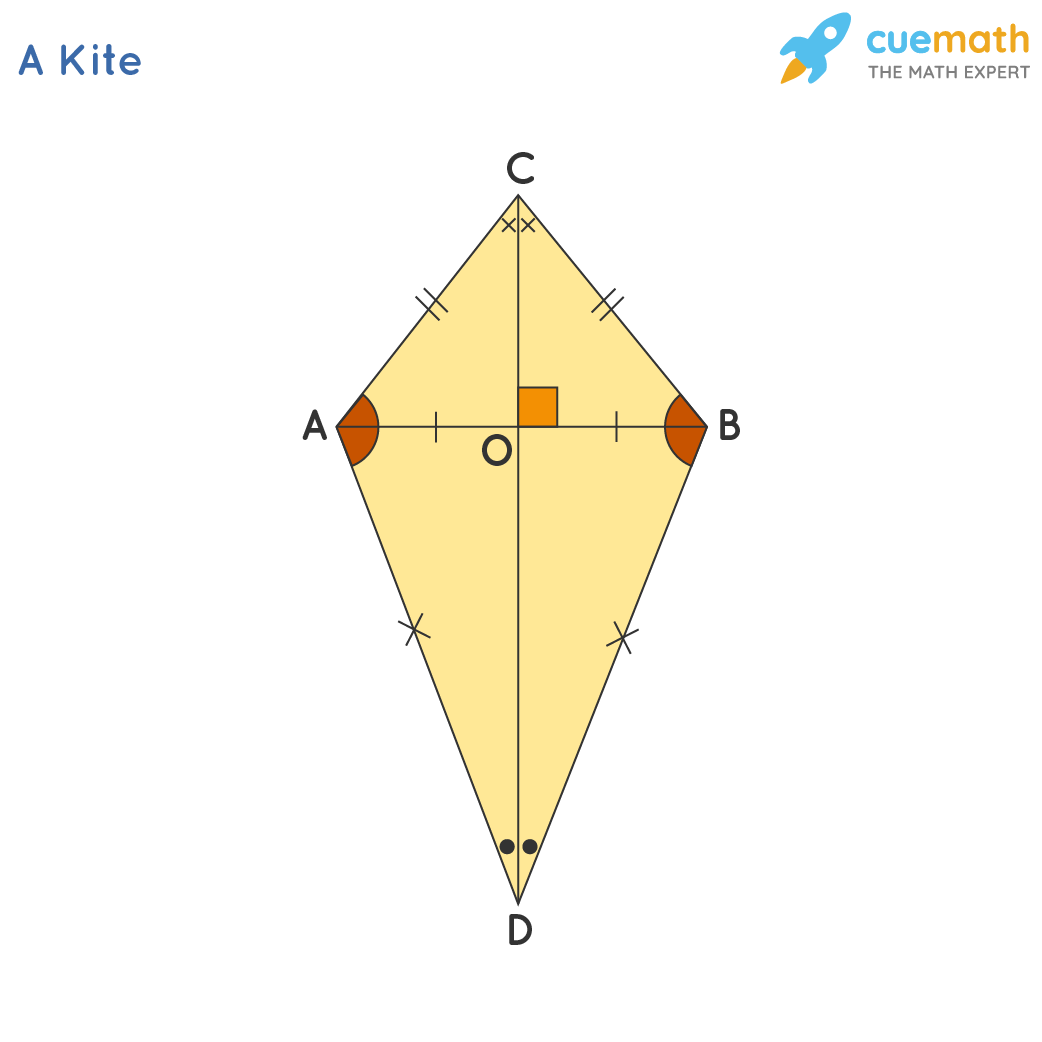
Property 1: Symmetry


Kites have one line of symmetry that runs through the two pairs of congruent, adjacent sides. This symmetry:
- Divides the kite into two congruent halves.
- Makes the diagonals perpendicular, intersecting at their midpoint.
- Is essential in understanding the angles and properties of the kite.
💡 Note: Symmetry is not just about looks; it’s a key element for proving many theorems involving kites.
Property 2: Diagonals


Kites possess diagonals with unique traits:
- The diagonals intersect at right angles.
- One diagonal bisects the other. The longer diagonal bisects the shorter one.
- The longer diagonal also bisects the angles at the vertices where it meets the non-congruent sides.
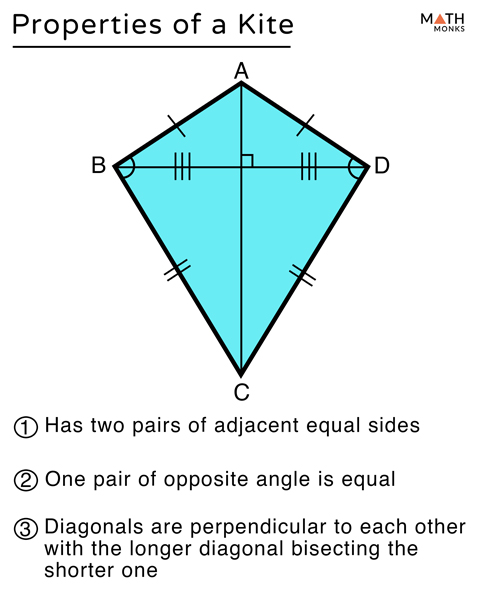
Property 3: Angle Bisectors

The diagonals of a kite are not just lines that connect opposite vertices; they also:
- Bisect the angles where they intersect with the non-congruent sides.
- Create two triangles on either side of the longer diagonal, which are mirror images of each other.
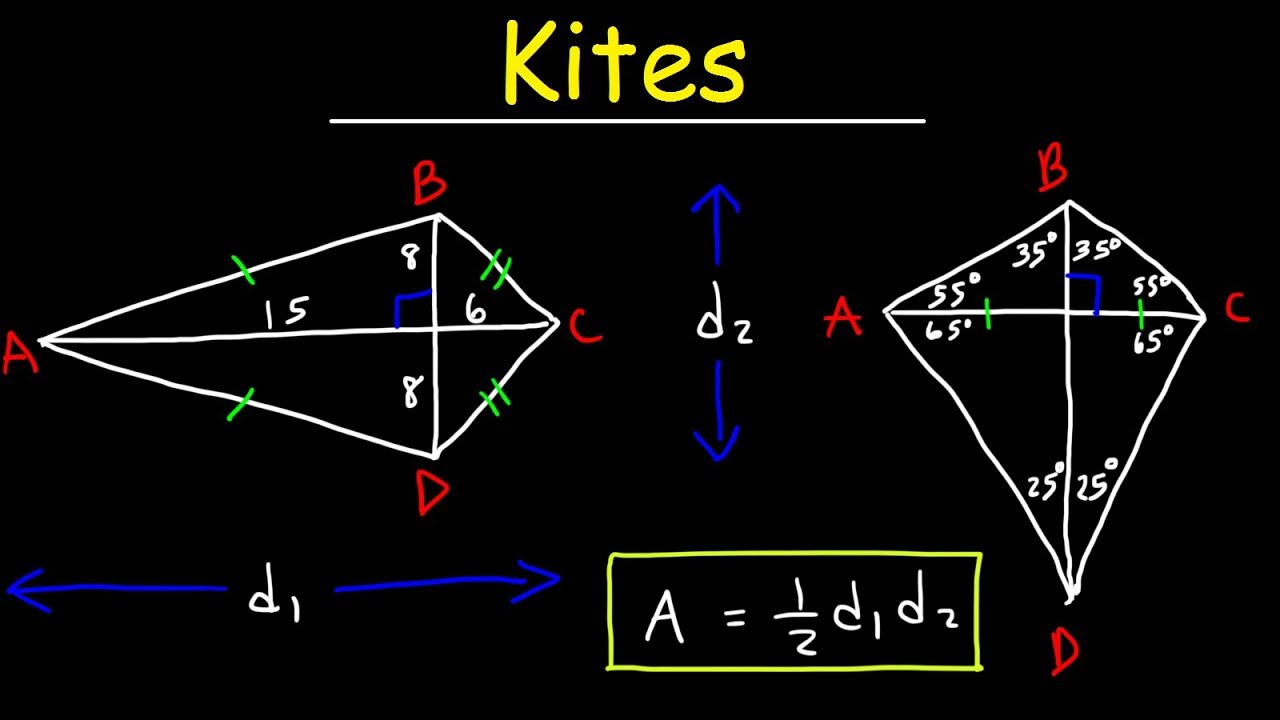
Property 4: Area Calculation

Calculating the area of a kite is straightforward but relies on the properties of its diagonals:
- Area = 0.5 × d1 × d2, where d1 and d2 are the lengths of the diagonals.
📏 Note: This method uses the fact that the diagonals intersect at right angles, making the formula valid for kites.
Property 5: Perimeter

The perimeter of a kite, while not as elegant as its area calculation, involves:
- Adding the lengths of the four sides.
- Considering the symmetry to simplify calculations if only the lengths of two sides are known.
These properties of kites not only define their mathematical identity but also serve as foundational knowledge for exploring more complex geometric shapes and solving problems involving symmetry, angles, and areas. Whether you're tackling proofs or designing intricate patterns, the understanding of kite properties is indispensable. They bridge the gap between basic shapes and more advanced geometric forms, offering insights into properties like diagonal relationships, angle bisectors, and symmetry, which are universal in geometric studies.
How do you prove that a quadrilateral is a kite?

+
To prove that a quadrilateral is a kite, you can show that it has one line of symmetry that divides it into two congruent triangles or demonstrate that two pairs of adjacent sides are congruent.
Can a kite have equal diagonals?
+
While kites typically have diagonals of different lengths, there are special cases like the rhombus where all sides are equal, and the diagonals are both equal and bisect each other at right angles.
What is the difference between a kite and a rhombus?

+
A rhombus is a special type of kite where all sides are equal in length. While both shapes share properties like perpendicular diagonals and symmetry, the rhombus’s unique trait is the equality of all its sides, making it a more specific case of a kite.
Why do the diagonals of a kite bisect each other at right angles?

+
The diagonals of a kite bisect each other at right angles due to the symmetry and congruent pairs of sides. This ensures that the two triangles formed by the diagonals are congruent and have a right angle at the intersection point.
How do you find the perimeter of a kite if you only know the lengths of two sides?

+
If you know the lengths of the two unequal sides (let’s call them ‘a’ and ‘b’), and due to symmetry, these sides are duplicated, the perimeter would be 2a + 2b.



