Master Precalculus Limits: Essential Worksheet Guide

Understanding the concept of limits is fundamental to mastering calculus, serving as the backbone for derivatives, integrals, and beyond. This comprehensive guide will explore various aspects of precalculus limits, offering a step-by-step worksheet to aid in your learning journey. Whether you're preparing for an exam, deepening your understanding, or embarking on a math-centric career, this guide will equip you with the tools needed to tackle limit problems effectively.
Why Limits Are Crucial in Precalculus

Limits lie at the heart of calculus, allowing mathematicians and scientists to analyze functions as they approach particular values or infinity. Here’s why understanding limits is essential:
- Foundation of Calculus: Limits form the basis for derivatives and integrals, which are key elements in calculus.
- Understanding Change: Limits help in understanding how functions change over small intervals, crucial for rates of change and optimization problems.
- Error Analysis: In applied sciences, limits are used to estimate errors in measurements or predictions.

Essential Limit Definitions and Properties

Before we delve into solving problems, let’s recap the definitions and key properties:
Definition of a Limit
The limit of a function ( f(x) ) as ( x ) approaches ( c ) is denoted as:
[ \lim_{x \to c} f(x) = L ]This means that as ( x ) gets arbitrarily close to ( c ), ( f(x) ) gets arbitrarily close to ( L ).
Key Properties of Limits
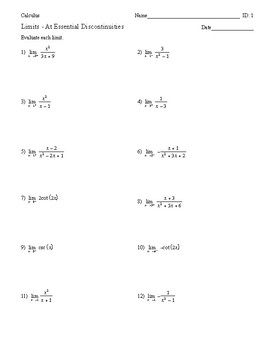
Here are some properties to keep in mind when solving limit problems:
| Property | Description |
|---|---|
| Sum Rule | ( \lim{x \to c} [f(x) + g(x)] = \lim{x \to c} f(x) + \lim{x \to c} g(x) ) |
| Difference Rule | ( \lim{x \to c} [f(x) - g(x)] = \lim{x \to c} f(x) - \lim{x \to c} g(x) ) |
| Product Rule | ( \lim{x \to c} [f(x) \cdot g(x)] = \lim{x \to c} f(x) \cdot \lim{x \to c} g(x) ) |
| Quotient Rule | ( \lim{x \to c} \frac{f(x)}{g(x)} = \frac{\lim{x \to c} f(x)}{\lim{x \to c} g(x)} ), provided ( \lim{x \to c} g(x) \neq 0 ) |
| Scalar Multiple Rule | ( \lim{x \to c} [c \cdot f(x)] = c \cdot \lim_{x \to c} f(x) ) |

💡 Note: These properties are useful in simplifying complex limit problems by breaking them down into manageable parts.
Step-by-Step Guide to Solving Limit Problems

Let’s go through a comprehensive worksheet designed to help you tackle various types of limit problems:
1. Direct Substitution

- If the function is continuous at the point where the limit is being taken, simply substitute the value into the function.
- Example: Find ( \lim_{x \to 2} (3x^2 - 5) ):
- Substitute ( x = 2 ): ( 3(2^2) - 5 = 3 \cdot 4 - 5 = 12 - 5 = 7 )
2. Factoring and Simplifying

- When direct substitution results in an indeterminate form (like ( \frac{0}{0} ) or ( \frac{\infty}{\infty} )), try to factor the expression to cancel out common terms.
- Example: Find ( \lim{x \to 3} \frac{x^2 - 9}{x - 3} ):
- Factor the numerator: ( \frac{(x - 3)(x + 3)}{x - 3} )
- Cancel ( x - 3 ): ( \lim{x \to 3} (x + 3) = 6 )
3. Rational Functions

- If the limit involves a rational function where direct substitution leads to an indeterminate form, consider rationalizing the numerator or the denominator.
- Example: Find ( \lim{x \to \infty} \frac{5x^2 + 3x}{2x^2 - 1} ):
- Divide both numerator and denominator by the highest power of ( x ), here ( x^2 ): ( \lim{x \to \infty} \frac{5 + \frac{3}{x}}{2 - \frac{1}{x^2}} = \frac{5}{2} )
4. Trigonometric Limits

- Trigonometric functions often require the use of known limits like ( \lim{x \to 0} \frac{\sin(x)}{x} = 1 ).
- Example: Find ( \lim{x \to 0} \frac{\tan(x) - x}{x^3} ):
- Use the series expansion: ( \tan(x) \approx x + \frac{x^3}{3} )
- Substitute and simplify: ( \frac{x + \frac{x^3}{3} - x}{x^3} = \frac{\frac{x^3}{3}}{x^3} = \frac{1}{3} )
5. Squeeze Theorem

- This theorem is useful when you can find two functions that “squeeze” the original function, ensuring the limit exists.
- Example: Find ( \lim{x \to 0} x^2 \sin(\frac{1}{x}) ):
- Since ( -1 \leq \sin(\frac{1}{x}) \leq 1 ), multiply by ( x^2 ) to get ( -x^2 \leq x^2 \sin(\frac{1}{x}) \leq x^2 ).
- Using ( \lim{x \to 0} -x^2 = 0 ) and ( \lim{x \to 0} x^2 = 0 ), by the Squeeze Theorem, ( \lim{x \to 0} x^2 \sin(\frac{1}{x}) = 0 ).
The journey through understanding and mastering precalculus limits involves not just memorizing formulas but also developing a deep conceptual understanding. This guide provides a foundation to approach limit problems systematically, but remember that practice is key to internalizing these concepts.
What are the most common mistakes in solving limit problems?

+
Common mistakes include not recognizing when direct substitution fails, improper factorization, neglecting the Squeeze Theorem when applicable, or incorrectly applying the properties of limits.
How important is it to know trigonometric limits?

+
Trigonometric limits are essential as they are foundational for calculus involving trigonometric functions, particularly in derivatives and integrals.
Can limits be used outside of mathematics?

+
Yes, limits are used in various fields like physics, engineering, and economics for analyzing behaviors, errors, and optimization under limiting conditions.