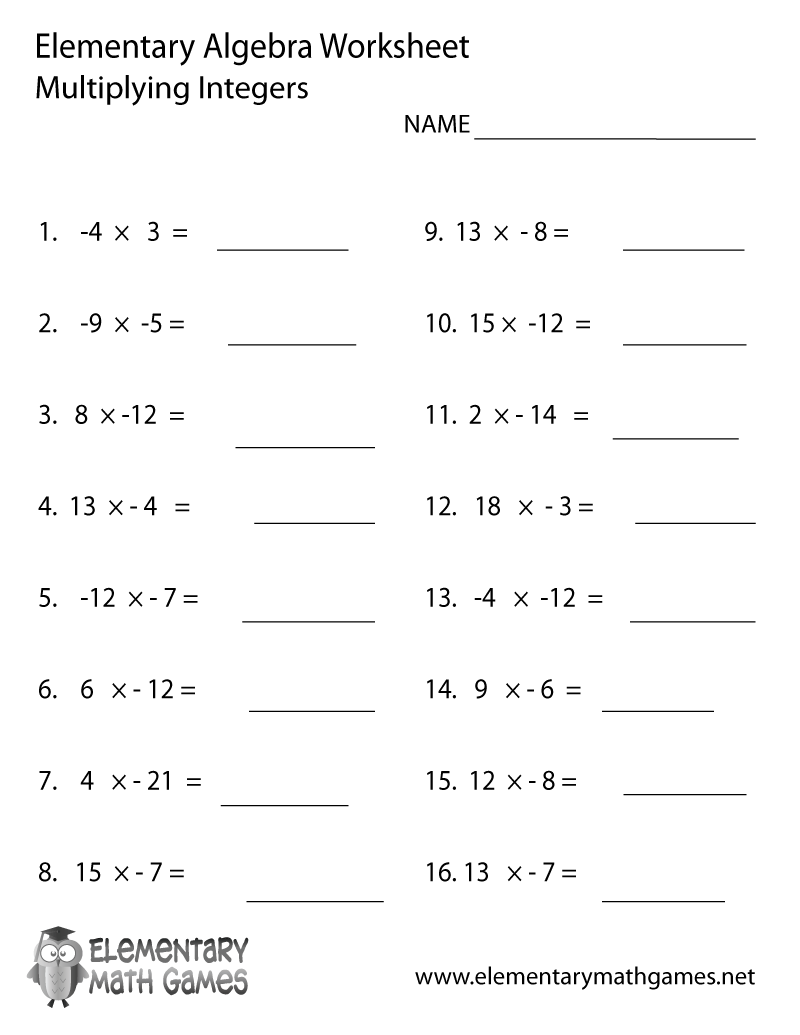5 Easy Steps to Factoring Quadratics with Answer Key

Factoring quadratics is a cornerstone skill in algebra that many students find challenging. However, with a clear method and some practice, it becomes much more manageable. This blog post aims to guide you through 5 easy steps to factoring quadratics, complete with examples and an answer key to help solidify your understanding.
Step 1: Identifying Quadratic Expressions

First, ensure you’re dealing with a quadratic equation, which has the form ax² + bx + c = 0 where a ≠ 0. Here are some key points to consider:
- The highest power of x must be 2.
- Coefficients a, b, and c can be any real number except a = 0.
- Look for any common factors to factor out.
Step 2: Factor Out Any Common Factors
Simplify your work by factoring out the greatest common factor (GCF) from all terms. This might not always be possible, but when it is, it significantly simplifies the expression. For example:
- Given 6x² + 12x:
- The GCF of 6 and 12 is 6, and the GCF of x² and x is x, so the GCF is 6x.
- Factoring out 6x, we get: 6x(x + 2).
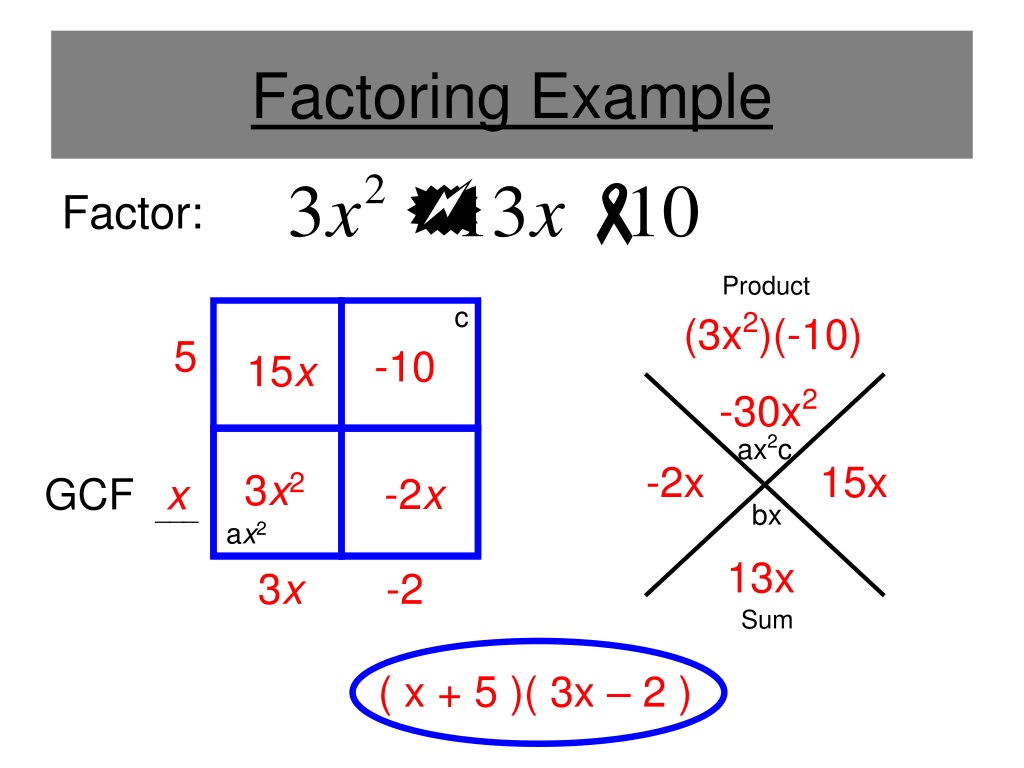
Step 3: The Factoring Technique

Now, you need to find two numbers that multiply to give the constant term © and add up to give the coefficient of the linear term (b). Let’s look at an example:
- Consider x² + 7x + 12
- Find two numbers that multiply to 12 © and add to 7 (b): These numbers are 3 and 4.
- Rewrite the middle term: x² + 3x + 4x + 12
- Group the terms: (x² + 3x) + (4x + 12)
- Factor each group: x(x + 3) + 4(x + 3)
- Combine using the distributive property: (x + 4)(x + 3)
Make sure you have followed each step:
🔍 Note: Always check your work by multiplying the factored form back to the original quadratic to ensure accuracy.
Step 4: Special Cases of Quadratics
Recognize special cases that simplify the factoring process:
| Special Case | Example |
|---|---|
| Perfect Square Trinomials | x² + 14x + 49 = (x + 7)² |
| Difference of Squares | x² - 9 = (x + 3)(x - 3) |

Step 5: Practice with an Answer Key

To reinforce your learning, here are some examples for you to factor:
- Factor x² + 5x + 6
- Answer: (x + 2)(x + 3)
- Factor 2x² + 14x + 24
- Answer: 2(x² + 7x + 12) = 2(x + 3)(x + 4)
- Factor x² - 16
- Answer: (x + 4)(x - 4)
By following these steps and practicing with real examples, you'll become more adept at factoring quadratics. The key is to recognize patterns and use the algebraic techniques provided. As you gain more experience, you'll find these steps becoming second nature.
What if the quadratic does not have two distinct factors?

+
Sometimes, a quadratic expression is a perfect square or cannot be factored into simpler terms with integer coefficients, indicating either one or no real solutions.
Can all quadratics be factored?

+
Not all quadratics can be factored into binomials over the integers. Some require using the quadratic formula or completing the square, which might result in irrational or complex roots.
What is the advantage of factoring quadratics?

+
Factoring allows us to solve equations more easily, find roots, and simplify complex expressions. It’s essential for understanding algebraic functions and their applications in higher mathematics.